Pure Recurring Decimal
Definition of Pure recurring decimal:
A decimal in which all the digits in the decimal part are repeated is called a pure recurring decimal.
A few solved problems are explained step-by-step with detailed explanation.
Worked-out example of pure recurring decimal:
(a) 5/3
= 1.666........
For, 5/3 when 5 is divided by 3, the quotient is 1.666.... and the digit 6 is repeating.
For instance, 1.666666 ......... can also be written as 1.6
Alternatively, we can write it by placing a dot above the repeating digit 6 in the quotient.
Therefore, 5/3 is a pure recurring decimal.
(b) 1/37
= 0.027027........
For, 1/37 when 1 is divided by 37, the quotient is 0.027027.... and the digits 027 are repeating.
For instance, 0.027027........ can also be written as 0.027
Alternatively, we can write it by placing a dot above the repeating digits 027 in the quotient.
Therefore, 1/37 is a pure recurring decimal.
(c) 9/37
= 0.243243......
For, 9/37 when 9 is divided by 37, the quotient is 0.243243....and the digits 243 are repeating.
For instance, 0.243243....... can also be written as 0.243
Alternatively, we can write it by placing a dot above the repeating digits 243 in the quotient.
Therefore, 9/37 is a pure recurring decimal.
● Related Concept
● Decimals
● Conversion of Unlike Decimals to Like Decimals
● Decimal and Fractional Expansion
● Converting Decimals to Fractions
● Converting Fractions to Decimals
● H.C.F. and L.C.M. of Decimals
● Repeating or Recurring Decimal
● BODMAS/PEMDAS Rules - Involving Decimals
● PEMDAS Rules - Involving Integers
● PEMDAS Rules - Involving Decimals
● BODMAS Rules - Involving Integers
● Conversion of Pure Recurring Decimal into Vulgar Fraction
● Conversion of Mixed Recurring Decimals into Vulgar Fractions
● Rounding Decimals to the Nearest Whole Number
● Rounding Decimals to the Nearest Tenths
● Rounding Decimals to the Nearest Hundredths
● Simplify Decimals Involving Addition and Subtraction Decimals
● Multiplying Decimal by a Decimal Number
● Multiplying Decimal by a Whole Number
● Dividing Decimal by a Whole Number
● Dividing Decimal by a Decimal Number
7th Grade Math Problems
From Pure recurring Decimal to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
2nd Grade Geometry Worksheet | Plane and Solid Shapes | Point | Line
Dec 14, 24 02:12 PM
2nd grade geometry worksheet -
2nd grade math Worksheets | Free Math Worksheets | By Grade and Topic
Dec 14, 24 12:25 PM
2nd grade math worksheets is carefully planned and thoughtfully presented on mathematics for the students. -
Patterns in Numbers | Patterns in Maths |Math Patterns|Series Patterns
Dec 13, 24 08:43 AM
We see so many patterns around us in our daily life. We know that a pattern is an arrangement of objects, colors, or numbers placed in a certain order. Some patterns neither grow nor reduce but only r… -
Patterns in Math | Missing Number | Counting Numbers | Worksheets
Dec 13, 24 12:31 AM
Finding patterns in math is very important to understand the sequence in the series. We need to find the exact missing number that from the group of numbers. The counting numbers may be counting -
Concept of Pattern | Similar Patterns in Mathematics | Similar Pattern
Dec 12, 24 11:22 PM
Concept of pattern will help us to learn the basic number patterns and table patterns. Animals such as all cows, all lions, all dogs and all other animals have dissimilar features. All mangoes have si…
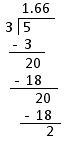
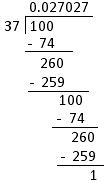
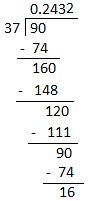
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.