Conversion of Fraction to Decimal Fraction
In conversion of fraction to decimal fraction the rules are discussed here.
(i) If it is a proper fraction, write the numerator as a decimal.
(ii) If it is a mixed fraction, convert it to an improper fraction.
(iii) Divide as usual. Add as many zeroes after the decimal to the numerator as required, to complete the division.
Let us consider some of the examples:
(i) Convert ½ to decimal.
Solution:
1 ÷ 2
Therefore, ½ = 0.5
(ii) Convert 2/5 to decimal
Solution:
2 ÷ 5
Therefore, 2/5 = 0.4
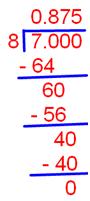
(iii) Convert 7/8 to decimal
Solution:
7 ÷ 8
Therefore, 7/8 = 0.875
A whole number is a decimal with as many decimal places as required
For example:
4 = 4.0
= 4.00
= 4.000
= 4.0000
All the above are equal to whole number 4.
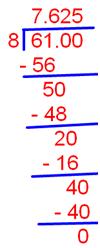
(iv) Convert 7 5/8 to decimal
Solution:
7 5/8
= (7 × 8 + 5)/8
= (56 + 5)/8
= 61/8
Therefore, 7 5/8 = 7.625
`
● Decimal.
Expanded form of Decimal Fractions.
Changing Unlike to Like Decimal Fractions.
Comparison of Decimal Fractions.
Conversion of a Decimal Fraction into a Fractional Number.
Conversion of Fractions to Decimals Numbers.
Addition of Decimal Fractions.
Problems on Addition of Decimal Fractions
Subtraction of Decimal Fractions.
Problems on Subtraction of Decimal Fractions
Multiplication of a Decimal Numbers.
Multiplication of a Decimal by a Decimal.
Properties of Multiplication of Decimal Numbers.
Problems on Multiplication of Decimal Fractions
Division of a Decimal by a Whole Number.
Division of Decimal Fractions by Multiples.
Division of a Decimal by a Decimal.
Division of a whole number by a Decimal.
Properties of Division of Decimal Numbers
Problems on Division of Decimal Fractions
Conversion of fraction to Decimal Fraction.
5th Grade Numbers Page
5th Grade Math Problems
From Conversion of Fraction to Decimal Fraction to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
|
|
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.