Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Division of Decimal Fractions
The rules of division of decimal fractions by 10, 100, 1000 etc. are discussed here.
(i) While dividing a decimal by 10, 100, or 1000 etc. i.e., multiples of 10, the decimal shifts to the left by as many places as there are zeroes in the divisor.
(ii) If the number of places in the integral part is less, then put the required number of zeroes to the left of the integral part, then shift the decimal point.
1. 71.6 ÷ 10
Solution:
71.6 ÷ 10
716/10 ÷ 10
= 716/10 × 1/10
= 716/100
= 71.6 ÷10
= 7.16
Therefore, 71.6 ÷ 10 = 7.16
Here we observe that decimal moves one place to the left.
2. 923.07 ÷ 100
Solution:
923.07 ÷ 100
= 92307/100 ÷ 100
= 92307/100 × 1/100
= 92307/10000
= 9.2307
Therefore, 923.07 ÷ 100 = 9.2307
Here we observe that decimal shifts two places to the left.
3. 44.008 ÷ 1000
Solution:
44.008 ÷ 1000
44.008/1000 ÷ 1000
= 44008/1000 × 1/1000
= 44008/1000000
=0.044008
Therefore, 44.008 ÷ 1000 = 0.044008
Here we observe that decimal point shifts three places to the left.
Let us consider some of the examples of division of decimal fractions by 10, 100, 1000, etc….
(i) 17.1 ÷ 10
Here the decimal shifts to the left by as many places as there are zeroes in the divisor.
Since there is 1 zero in the divisor then the decimal shifts 1 place to the left.
Therefore, 17.1 ÷ 10 = 1.71
(ii) 42.08 ÷ 10
Since there is 1 zero in the divisor then the decimal shifts 1 place to the left.
Therefore, 42.08 ÷ 10 = 4.208
(iii) 2.1 ÷ 100
We observe that the number of places in the integral part is less, then put the required number of zeroes to the left of the integral part, then shift the decimal point.
Since there are 2 zeroes in the divisor then the decimal shifts 2 places to the left.
Therefore, 2.1 ÷ 100 = 0.021
(iv) 73.3 ÷ 100
We observe that the number of places in the integral part is less, then put the required number of zeroes to the left of the integral part, then shift the decimal point.
Since there are 2 zeroes in the divisor then the decimal shifts 2 places to the left.
Therefore, 73.3 ÷ 100 = 0.733
(v) 81.6 ÷ 1000
We observe that the number of places in the integral part is less, then put the required number of zeroes to the left of the integral part, then shift the decimal point.
Since there are 3 zeroes in the divisor then the decimal shifts 3 places to the left.
Therefore, 81.6 ÷ 1000 = 0.0816
(vi) 984.72 ÷ 1000
We observe that the number of places in the integral part is less, then put the required number of zeroes to the left of the integral part, then shift the decimal point.
Since there are 3 zeroes in the divisor then the decimal shifts 3 places to the left.
Therefore, 984.72 ÷ 1000 = 0.98472
● Choose the right answer and fill in the blank.
(i) 478.65 ÷ ________ = 47.865
(a) 10
(b) 100
(c) 1000
(d) 1
Answer: (a) 10
(ii) 137.85 × 10 = ________
(a) 13785
(b) 13.785
(c) 1378.5
(d) 1.3785
Answer: (c) 1378.5
● Decimal.
- Tenth Place in Decimals
- Hundredths Place in Decimals
- Thousandths Place in Decimals
- Whole Numbers and Decimals
- Decimal Place Value Chart.
- Expanded form of Decimal Fractions
- Like Decimal Fractions.
- Unlike Decimal Fraction.
- Equivalent Decimal Fractions.
- Changing Unlike to Like Decimal Fractions.
- Ordering Decimals
- Comparison of Decimal Fractions.
- Conversion of a Decimal Fraction into a Fractional Number.
- Conversion of Fractions to Decimals Numbers.
- Addition of Decimal Fractions.
- Problems on Addition of Decimal Fractions
- Subtraction of Decimal Fractions.
- Problems on Subtraction of Decimal Fractions
- Multiplication of a Decimal Numbers.
- Multiplication of a Decimal by 10, 100, 1000
- Multiplication of a Decimal by a Decimal.
- Properties of Multiplication of Decimal Numbers.
- Problems on Multiplication of Decimal Fractions
- Division of a Decimal by a Whole Number.
- Division of Decimal Fractions
- Division of Decimal Fractions by Multiples.
- Division of a Decimal by a Decimal.
- Division of a whole number by a Decimal.
- Properties of Division of Decimal Numbers
- Problems on Division of Decimal Fractions
- Conversion of fraction to Decimal Fraction.
- Simplification in Decimals.
- Word Problems on Decimal.
5th Grade Numbers Page
5th Grade Math Problems
Erom Division of Decimal Fractions to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.

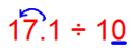
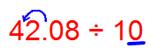
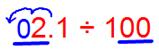
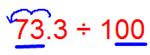
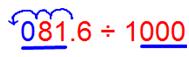
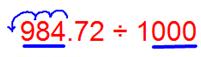


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.