5th Grade Decimals

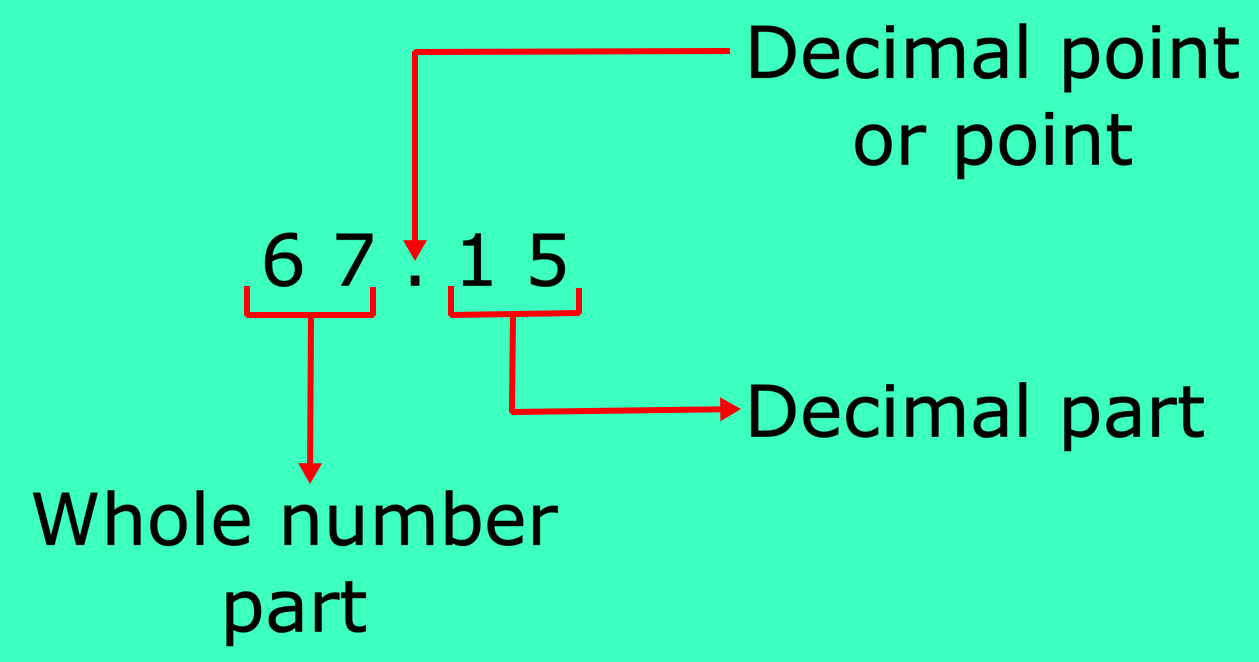
A fractional number whose denominator is 10 or multiple of 10 is called a decimal. Every decimal has two parts whole number part and decimal part. These two parts are separated by a dot or point. This dot or point is known as decimal point.

For example, 51.731 is decimal. Here 51 is the whole part and 731 is the decimal part.

Our counting number system has 10 digits to write all numbers using place-values. We know that the position of a digit in the number determines its value in the number. Each place in the place-value chart is 10 times greater than the place to its right.

For example; 10 ones = 1 ten, 10 tens = 1 hundred, 10 hundreds = 1 thousand. Let us now extend the place-value idea developed for whole numbers to fractional part of a whole number. The places to the right of the ones place are called decimal places. Each place is ten times smaller than the one to its immediate left. So, the place value of a digit becomes \(\frac{1}{10}\) when we move one place towards the right.

How to read a decimal?

The length of a pencil is 17.2 cm. This is read as seventeen point two cm.

A decimal is read in two ways:

(i) 43.814 is read as forty three point eight, one, four.

(ii) 43.814 is read as forty three and eight hundred fourteen thousandths.

How to write a fractional number as decimals?

7/10 = .07

2179/1000 = 2.179

DECIMAL FRACTIONS

Some fractions have denominators 10, 100, 1000 and so on.

For example, \(\frac{3}{10}\), \(\frac{7}{100}\), \(\frac{9}{1000}\)

We can represent these fractions as follows.

\(\frac{3}{10}\) = 0.3

\(\frac{7}{100}\) = 0.07 

\(\frac{9}{1000}\) =0.009

Such fractions are called decimal fractions.

DECIMAL SYSTEM

Decimal system is a system of measurement with units that are related to each other by multiples of 10. In this system, the place values of the digits in a number correspond to multiples of 10.

We can represent a fractional number as a decimal. Decimal system is based on 10. The numbers like 4.2, 12.05, 29.009 are called decimals. A decimal has two parts.

Sometime, a decimal has 0 as whole number. For example, 0.3, 0.9, 0.23, 0.68, etc.

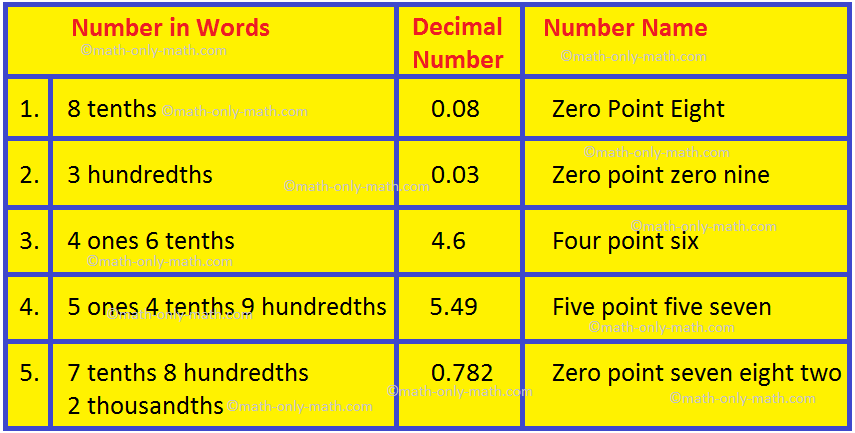
Write the decimal number in the table below:

How to write a decimal as fractional numbers?

To convert a decimal number 49.50 into a fraction, 49.50 = 4950/100.

Similarly,

(i) 1.1 = 11/10

(ii) 2.13 = 213/100

(iii) 17.2 = 172/10

(iv) 14.11 = 1411/100

(v) 9.781 = 9781/1000

So, from the above explanation we conclude that the number is divided:

(a) by 10 if there is one digit after the decimal.

(b) by 100 if there is two digits after the decimal.

(c) by 1000 if there is three digits after the decimal.

(d) by 10000 if there is three digits after the decimal and so on.

(a) The number is divided by 10 if there is one digit after the decimal.

For example:

(i) 1.5 = 15/10

[We observe that in 1.5, after the decimal there is one digit so we need to divide by 10]


(ii) 12.3 = 123/10

[We observe that in 12.3, after the decimal there is one digit so we need to divide by 10]


(iii) 10.1 = 101/10

[We observe that in 10.1, after the decimal there is one digit so we need to divide by 10]


(iv) 111.2 = 1112/10

[We observe that in 111.2, after the decimal there is one digit so we need to divide by 10]


(v) 145.9 = 1459/10

[We observe that in 145.9, after the decimal there is one digit so we need to divide by 10]

(b) The number is divided by 100 if there is two digits after the decimal.

For example:

(i) 2.51 = 251/100

[We observe that in 2.51, after the decimal there is two digits so we need to divide by 100] 


(ii) 12.03 = 1203/100

[We observe that in 12.03, after the decimal there is two digits so we need to divide by 100] 


(iii) 19.11 = 1911/100

[We observe that in 19.11, after the decimal there is two digits so we need to divide by 100] 


(iv) 11.24 = 1124/100

[We observe that in 11.24, after the decimal there is two digits so we need to divide by 100] 


(v) 14.93 = 1493/100

[We observe that in 14.93, after the decimal there is two digits so we need to divide by 100] 



(c) The number is divided by 1000 if there is three digits after the decimal.

For example:

(i) 1.555 = 1555/1000

[We observe that in 1.555, after the decimal there is three digits so we need to divide by 1000] 


(ii) 12.005 = 12005/1000

[We observe that in 12.005, after the decimal there is three digits so we need to divide by 1000]


(iii) 2.001 = 2001/1000

[We observe that in 2.001, after the decimal there is three digits so we need to divide by 1000] 


(iv) 1.112 = 1112/1000

[We observe that in 1.112, after the decimal there is three digits so we need to divide by 1000] 


(v) 15.913 = 15913/1000

[We observe that in 15.913, after the decimal there is three digits so we need to divide by 1000] 

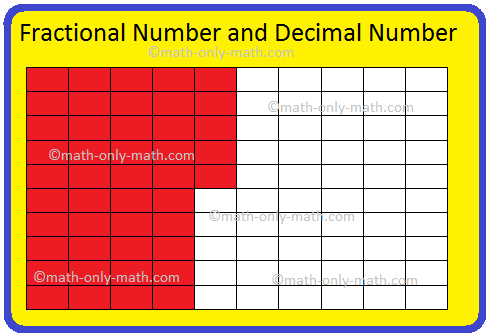
I. Write the fractional number and decimal number for the shaded part of the figure.

We see that the sheet is divided into 100 equal parts. Each part represents one-hundredths of the whole. 

Among the 100 parts the shaded part is 45.

So, we can represent the figure in fractional form as \(\frac{45}{100}\) and in decimal form as 0.45, where 4 represents 4 tenths and 5 represents 5 hundredths.

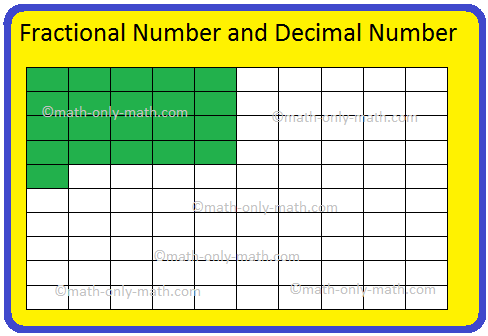
II. Write the fractional number and decimal number for the shaded part of the figure.

We see that the sheet is divided into 100 equal parts. Each part represents one-hundredths of the whole. 

Among the 100 parts the shaded part is 21.

So, we can represent the figure in fractional form as \(\frac{21}{100}\) and in decimal form as 0.21, where 2 represents 2 tenths and 1 represents 1 hundredths.

III. Write the fractional number and decimal number for the shaded part of the figure.

We see that the sheet is divided into 1000 equal parts. Each part represents one-hundredths of the whole. 

Among the 1000 parts the shaded part is 18.

So, we can represent the figure in fractional form as \(\frac{18}{1000}\) and in decimal form as 0.018, where 0 represents 0 tenths, 1 represents 1 hundredths and 8 represents 8 thousandths.

Worksheet on 5th Grade Decimals

Practice Problems on Decimals:

1. Name the following decimal numbers.

(i) 0.9

(ii) 197.33

(iii) 0.57

(iv) 72.465

(v) 35.064

(vi) 84.06

Answers:

(i) Zero point nine

(ii) One hundred ninety seven point three three

(iii) Zero point five seven

(iv) Seventy two point four six five

(v) Thirty five point zero six four

(vi) Eighty four point zero six

2. Tick (✓) the decimal fractions and cross (❌) the others.

(i) \(\frac{2}{10}\)          ▢

(ii) \(\frac{4}{5}\)          ▢

(iii) \(\frac{1}{7}\)          ▢

(iv) \(\frac{3}{100}\)          ▢

(v) \(\frac{7}{10}\)          ▢

(vi) \(\frac{7}{9}\)          ▢

(vii) \(\frac{72}{1000}\)          ▢

(viii) \(\frac{25}{42}\)          ▢

(ix) \(\frac{19}{25}\)          ▢

(x) \(\frac{9}{10}\)          ▢

(xi) \(\frac{57}{65}\)          ▢

(xii) \(\frac{31}{100}\)          ▢

2. (i) ✓

(ii) ❌

(iii) ❌

(iv) ✓

(v) ✓

(vi) ❌

(vii) ✓

(viii) ❌

(ix) ❌

(x) ✓

(xi) ❌

(xii) ✓

●Decimal.

• Tenth Place in Decimals
  
• Decimal Place Value Chart.
• Expanded form of Decimal Fractions.
• Like Decimal Fractions.
• Unlike Decimal Fraction.
• Equivalent Decimal Fractions.
• Changing Unlike to Like Decimal Fractions.
• Ordering Decimals
• Comparison of Decimal Fractions.
• Conversion of a Decimal Fraction into a Fractional Number.
• Conversion of Fractions to Decimals Numbers.
• Addition of Decimal Fractions.
• Problems on Addition of Decimal Fractions
• Subtraction of Decimal Fractions.
• Problems on Subtraction of Decimal Fractions
• Multiplication of a Decimal Numbers.
• Multiplication of a Decimal by a Decimal.
• Properties of Multiplication of Decimal Numbers.
• Problems on Multiplication of Decimal Fractions
• Division of a Decimal by a Whole Number.
• Division of Decimal Fractions
• Division of Decimal Fractions by Multiples.
• Division of a Decimal by a Decimal.
• Division of a whole number by a Decimal.
• Properties of Division of Decimal Numbers
• Problems on Division of Decimal Fractions
• Conversion of fraction to Decimal Fraction.
• Simplification in Decimals.
• Word Problems on Decimal.

5th Grade Numbers Page

5th Grade Math Problems

From 5th Grade Decimals to HOME PAGE