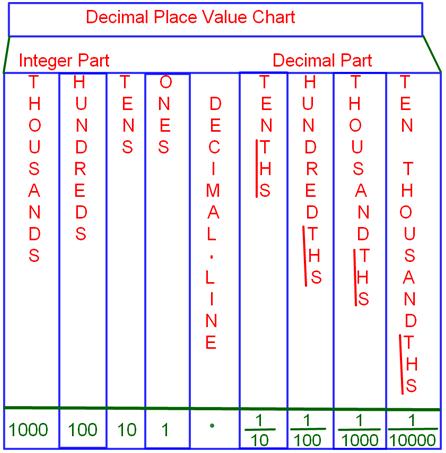
Decimal Place Value Chart

Decimal place value chart are discussed here:

We know that in a place value chart, each place has a value ten times the value of the next place on its right.

For example, the value of hundreds place is ten times of the value of tens place, the value of thousands place is ten times of the value of hundreds place etc.

In other words, the value of a place is one-tenth (\(\frac{1}{10}\)) of the value of the next place on its left.

For example, the value of hundreds place is one-tenth (\(\frac{1}{10}\)) of the value of thousands place, the value of tens place is one-tenth of the value of hundreds place, etc.

The first place after the decimal is got by dividing the number by 10; it is called the tenths place.

The second place after the decimal is got by dividing the number by 100; it is called the hundredths place.


The third place after the decimal is got by dividing the number by 1000; it is called the thousandths place.

Consider the place value of 7 in the following:

7598 ⟶ The place value of 7 is 7000;

5720 ⟶ The place value of 7 is 700.

4579 ⟶ The place value of 7 is 70 and

9467 ⟶ The place value of 7 is 7.

We see that when the digit 1 moves one place to the right, its value becomes one-tenth (\(\frac{1}{10}\)) of its previous value; when it moves two places to the right, its value becomes one-hundredth (\(\frac{1}{100}\)) of its previous value and so on.

If we wish to continue moving towards right, we shall have to extend the place-value chart beyond ones place by opening the places for tenths, hundredths, thousandths and so on.

Decimal Place Value Chart:

If we represent the number 54 + \(\frac{7}{10}\) + \(\frac{3}{100}\) in the place value chart, then 5 goes to tens place, 4 goes to ones place, 7 goes to tenths place and 3 goes to hundredths place as indicated below.

The number shown in the table is written as 54.73 and is called a decimal fraction or simply decimal.

It is read as fifty four point seven three. The dot (.) is called the decimal point, and it separates whole number and fractional parts.

Similarly, the number 849 + \(\frac{3}{10}\) + \(\frac{1}{100}\) + \(\frac{5}{1000}\) is written as 849.315  and read as eight hundred forty nine point three one five. 

It can also be read as eight hundred forty nine and three hundred fifteen thousandths.

Note that while reading a decimal number, its decimal part is read digit-wise.

4.2 ⟶ Four point two

43.64 ⟶ Forty three point six four

0.45 ⟶ Zero point four five

731.09 ⟶ Seven hundred thirty one point zero nine

A decimal contains a whole number part and a decimal part.

In 4.2, the whole number part is 4 and the decimal part is 2.

In 43.64, the whole number part is 43 and the decimal part is 64.

In 0.45, the whole number part is 0 and the decimal part is 45.

In 731.09, the whole number part is 731 and the decimal part is 09

Note:

The decimal consisting of only one part, i.e., either decimal part or whole number part can be written by making use of zero in whole or decimal part.

For Example:

37 can be written as 37.0,

.49 can be written as 0.49, etc.

Decimal Places:

The number of digits in the decimal part of decimal gives the number of decimal places.

For example, decimals 87.56 and 4.325 have two and three decimal places respectively.

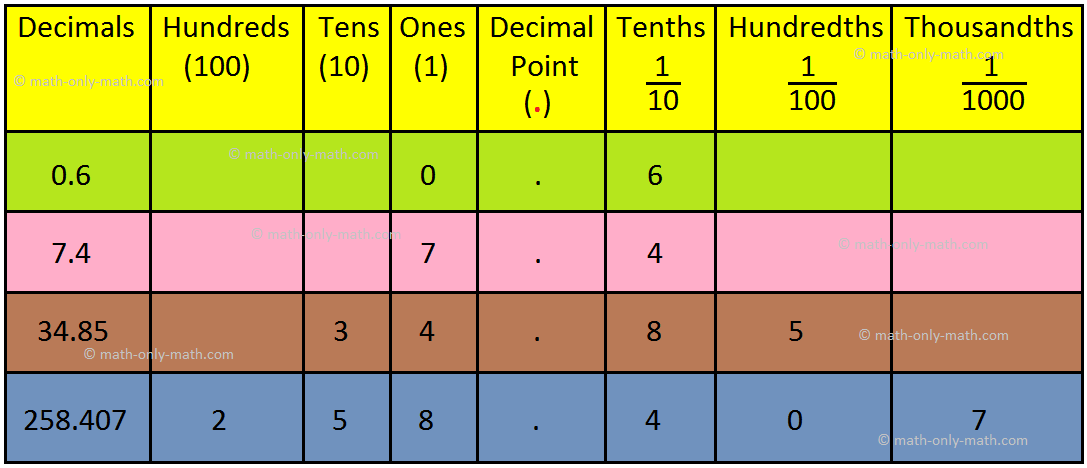
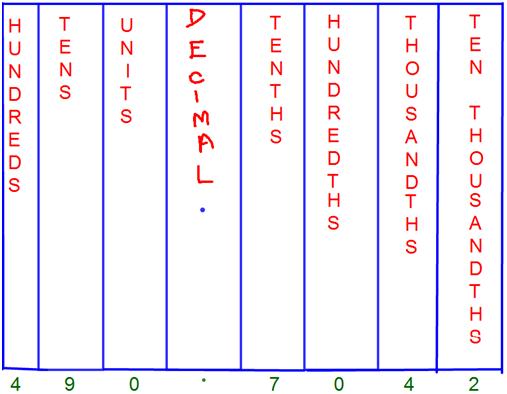
1. Arrange the following decimals in the place value chart.

0.6;  7.4;  34.85;  258.407

Solution:

The given decimals written in the place value chart are as follows:

2. Write the following decimals in words.

(i) 6.2

(ii) 38.76

(iii) 419.317

Solution:

(i) 6.2 is written as 6\(\frac{2}{10}\) and is read as 'six point two' or 'six and two tenths or six decimal two.

(ii) 38.76 is written as 38\(\frac{76}{100}\) and is read as 'thirty-eight point seven six' or 'thirty-eight and seventy-six hundredths'.

(iii) 419.317 is written as 419\(\frac{317}{1000}\) and is read as 'four hundred nineteen point three one seven' or 'four hundred nineteen and three hundred seventeen thousandths'.

Solved Examples on Decimal Place Value Chart:

1. How to write the place value of the digit 45.123?

The place of 3 in the decimal 45.123 is \(\frac{3}{1000}\).

The place of 2 in the decimal 45.123 is \(\frac{2}{100}\)

The place of 1 in the decimal 45.123 is \(\frac{1}{10}\)

The place of 5 in the decimal 45.123 is 5

The place of 4 in the decimal 45.123 is 40

Let us consider the following examples.

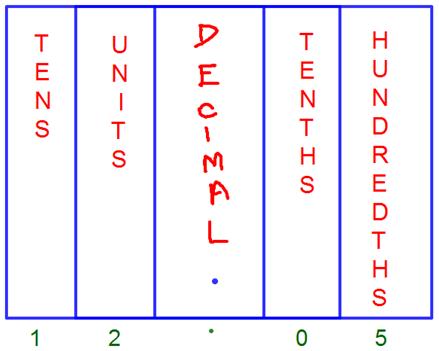
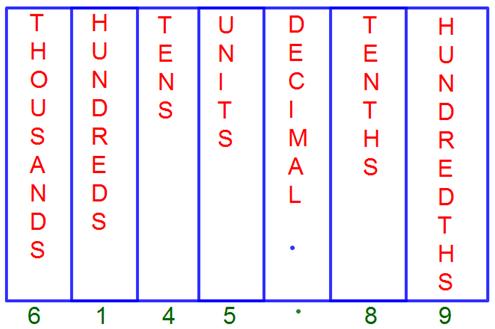
2. Write the following numbers in the decimal place value chart.

(i) 1.2

Solution:

1.2 in the decimal place value chart.

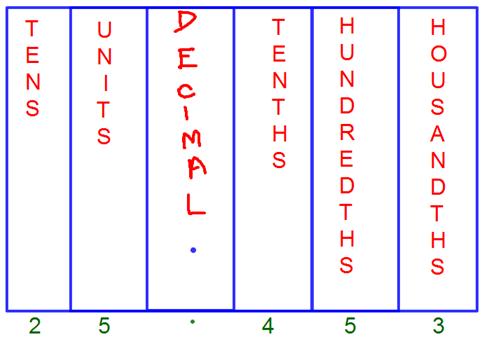
(ii) 12.05

Solution:

12.05 in the decimal place value chart.

(iii) 25.453

Solution:

25.453 in the decimal place value chart.

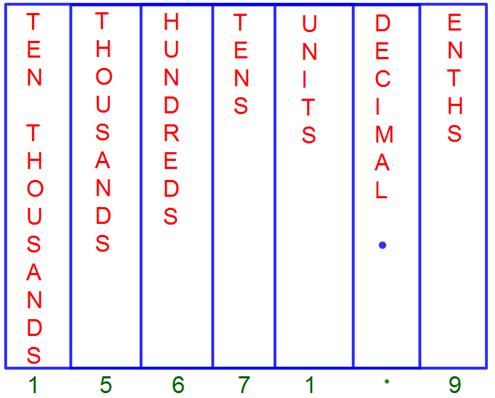
(iv) 490.7042

Solution:

490.7042 in the decimal place value chart.

(v) 6145.89

6145.89 in the decimal place value chart.

Solution:

(vi) 15671.9

Solution:

15671.9 in the decimal place value chart.

3. Write the place value of digit 7 in each of the following decimals:

(i) 513.073

The place of 7 in the decimal 513.073 is \(\frac{7}{100}\) or 7 hundredths.

(ii) 71.234

The place of 7 in the decimal 71.234 is 70 or 7 tens.

Worksheet on Decimal Place Value Chart

I. Find the place value of coloured digits of the following numbers.

(i) 2.473

(ii) 5.26

(iii) 3.089

(iv) 6.173

(v) 4.638

(vi) 9.725

(vii) 1.070

(viii) 5.158

(ix) 8.136

(x) 4.573

(xi) 2.009

(xii) 6.725

Answer:

I. (i) 0.400

(ii) 0.06

(iii) 0.080

(iv) 0.003

(v) 0.600

(vi) 0.020

(vii) 0.070

(viii) 0.100

(ix) 0.006

(x) 0.070

(xi) 0.009

(xii) 0.700

Practice Problems on Decimal Place Value Chart:

1. Identify the place value of the underlined digit in the given numbers.

(i) 65.71

(ii) 308.88

(iii) 716.927

(iv) 8546.293

(v) 4665.705

Answers:

(i) 1 hundredth

(ii) 3 hundreds

(iii) 9 tenths

(iv) 3 thousandths

(v) 4 thousands

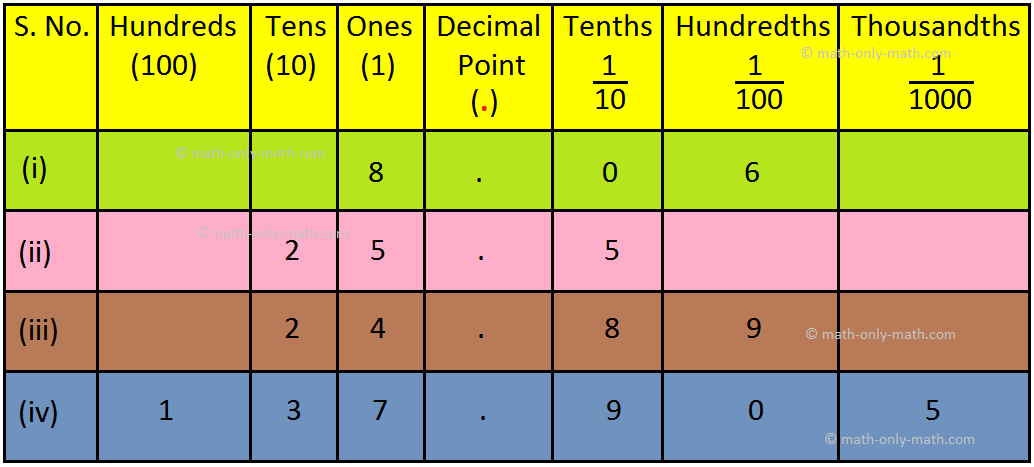
2. Write in the place value chart.

(i) 8.06

(ii) 25.5

(iii) 24.89

(iv) 137.905

Answer:

2.

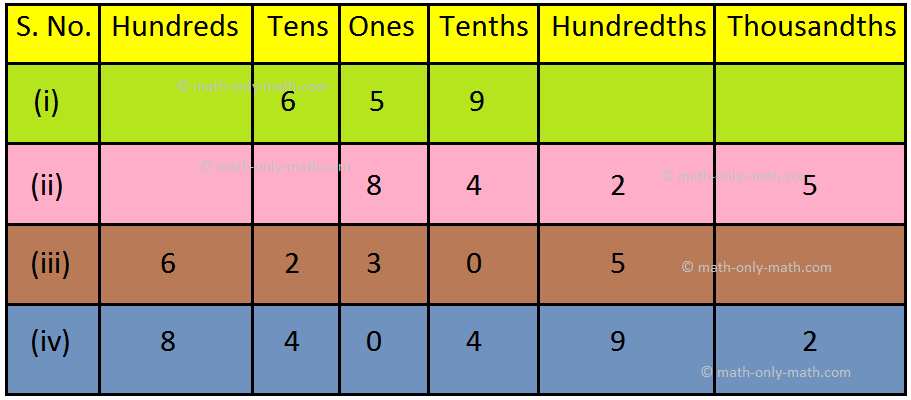
3. Write the decimals shown in the following place value table:

Answer:

3. (i) 65.9

(ii) 8.425

(iii) 623.05

(iv) 840.492

● Decimal.

Decimal Place Value Chart.

Expanded form of Decimal Fractions.

Like Decimal Fractions.

Unlike Decimal Fraction.

Equivalent Decimal Fractions.

Changing Unlike to Like Decimal Fractions.

Ordering Decimals

Comparison of Decimal Fractions.

Conversion of a Decimal Fraction into a Fractional Number.

Conversion of Fractions to Decimals Numbers.

Addition of Decimal Fractions.

Problems on Addition of Decimal Fractions

Subtraction of Decimal Fractions.

Problems on Subtraction of Decimal Fractions

Multiplication of a Decimal Numbers.

Multiplication of a Decimal by a Decimal.

Properties of Multiplication of Decimal Numbers.

Problems on Multiplication of Decimal Fractions

Division of a Decimal by a Whole Number.

Division of Decimal Fractions

Division of Decimal Fractions by Multiples.

Division of a Decimal by a Decimal.

Division of a whole number by a Decimal.

Properties of Division of Decimal Numbers

Problems on Division of Decimal Fractions

Conversion of fraction to Decimal Fraction.

Simplification in Decimals.

Word Problems on Decimal.

5th Grade Numbers

5th Grade Math Problems

From Decimal Place Value Chart to HOME PAGE