Simplification in Decimals
Simplification in decimals can be done with the help of PEMDAS Rule.
PEMDAS Rule Table
From the above chart we can observe that first we have to work on "P or Parentheses" and then on "E or Exponents", then from left to right doing either "Multiplication" or "Division" as we find them in the question.
Then from left to right doing either "Addition" or "Subtraction" as we find them we need to solve them accordingly.
Let us consider some of the examples on simplification in decimals:
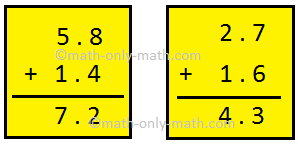
1. Solve 5.8 – 2.7 + 1.4 – 1.6
Solution:
We first group the numbers having same signs and then add them. Subtract the sum of the numbers with – sign from the sum of the numbers with + sign.
First step: Add 5.8, 1.4 and 2.7 and 1.6
Second step: Now subtract 4.3 from 7.2
Hence, 5.8 – 2.7 + 1.4 – 1.6 = 2.9
2. 4.5 + 3.7 – 3.6 ÷ 1.2
Solution:
4.5 + 3.7 – 3.6 ÷ 1.2
= 4.5 + 3.7 – 3.0
= 8.2 – 3.0
= 5.2
Answers: 5.2
3. 3 ÷ 16 + 1.2 × \(\frac{1}{4}\) - {\(\frac{1}{5}\) + (1 - 0.8) }
Solution:
3 ÷ 16 + 1.2 × \(\frac{1}{4}\) - {\(\frac{1}{5}\) + (1 - 0.8) }
3 ÷ 16 + 1.2 × \(\frac{1}{4}\) - {\(\frac{1}{5}\) + 1 - 0.8}
= 3 ÷ 16 + 1.2 × \(\frac{1}{4}\) - {\(\frac{1 + 5 - 4.0}{5}\)}
= 3 ÷ 16 + 1.2 × \(\frac{1}{4}\) - {\(\frac{6 - 4}{5}\)}
= 3 ÷ 16 + 1.2 × \(\frac{1}{4}\) - {\(\frac{2}{5}\)}
= 3 ÷ 16 + 1.2 × \(\frac{1}{4}\) - \(\frac{2}{5}\)
= \(\frac{3}{16}\) + \(\frac{1.2}{4}\) – \(\frac{2}{5}\)
= \(\frac{15 + 24 - 32}{80}\)
= \(\frac{7}{80}\)
= 0.0875
Answers: 0.0875
● Decimal
Expanded form of Decimal Fractions
Changing Unlike to Like Decimal Fractions
Comparison of Decimal Fractions
Conversion of a Decimal Fraction into a Fractional Number
Conversion of Fractions to Decimals Numbers
Subtraction of Decimal Fractions
Multiplication of a Decimal Numbers
Multiplication of a Decimal by a Decimal
Properties of Multiplication of Decimal Numbers
Division of a Decimal by a Whole Number
Division of Decimal Fractions by Multiples
Division of a Decimal by a Decimal
Division of a whole number by a Decimal
Conversion of fraction to Decimal Fraction
5th Grade Numbers
5th Grade Math Problems
From Simplification in Decimals to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
5th Grade Prime and Composite Numbers | Definitions | Examples | Math
Mar 21, 25 12:18 AM
5th grade prime and composite numbers -
14 Times Table | Read and Write Multiplication Table of 14| Video
Mar 20, 25 04:03 PM
In 14 times table we will learn how to read and write multiplication table of 14. We read fourteen times table as:One time fourteen is 14 Two times fourteen are 28 Three times fourteen are 42 -
5th Grade Test of Divisibility Rules | Divisibility Rules From 2 to 12
Mar 20, 25 04:00 PM
In 5th grade test of divisibility rules we will learn about the exact divisibility of a number by the numbers from 2 to 12. The digit in the ones place should be 2, 4, 6, 8 or 0. -
5th Grade Even and Odd Numbers | Definitions | Examples
Mar 20, 25 02:45 AM
Numbers which are exactly divisible by 2 are even numbers. For example. 2,4,6,8,20,48,88, etc. are even numbers. They are multiples of 2. Numbers which are not exactly divisible by 2 are odd numbers… -
5th Grade Factors and Multiples | Definitions | Solved Examples | Math
Mar 20, 25 01:02 AM
Here we will discuss how factors and multiples are related to each other in math. A factor of a number is a divisor which divides the dividend exactly. A factor of a number which is a prime number is…
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.