Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Dividing 3-Digit by 1-Digit Number
Dividing 3-Digit by 1-Digit Numbers are discussed here step-by-step.
How to divide 3-digit numbers by single-digit numbers?
Let us follow the examples to learn to divide 3-digit number by one-digit number.
I: Dividing 3-digit Number by 1-Digit Number without Remainder:
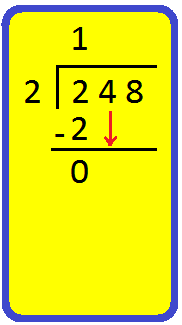
1. Divide 248 by 2 and verify the result.
Solution:
We proceed as follows:
Step I: Arrange the two given numbers as shown.
Step II: Divide 2 hundreds by 2.
|
Start by looking at the first number (hundreds place) in the dividend. Find a number in the table of 2 less than or equal to 2 We know 2 × 1 = 2. So, 1 is the required number. 2 × 1 = 2, write 1 in hundreds place of the quotient and 2 below 2. Subtract the number you got by multiplying the divisor, from the number in the dividend. Subtract 2 from 2 2 - 2 = 0 |
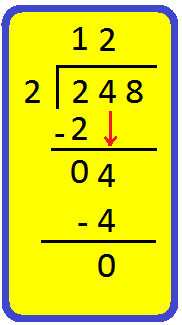
Step III: Divide 4 tens by 2.
|
Bring down the next digit, from the number in the dividend. We have 4 there; now find a number in the table of 2 that divides it. 2 × 1 = 2 2 × 2 = 4 So, 2 is the required number. 2 × 2 = 4, write 2 in tens place of the quotient and 4 below 4. |
Subtract the number you got by multiplying the divisor, from the number in the dividend.
Subtract 4 from 4
4 - 4 = 0
Step IV: Divide 8 ones by 2.
Bring down 8
Now see where does 8 come in the table of 2.
2 × 1 = 2
2 × 2 = 4
2 × 3 = 6
2 × 4 = 8
White 4 in the quotient and 8 under 8 and subtract.
8 - 8 = 0
Therefore, 248 ÷ 2 = 124
Dividing 3-Digit by 1-Digit Number Video
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
II: Dividing a 3-digit Number by a 1-Digit Number with Remainder: (Long Division)
Let us follow the examples to learn to divide 3-digit numbers by one-digit number with remainder.
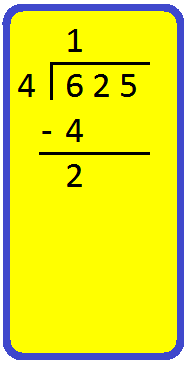
1. Divide the following and verify the result: Long Division
625 ÷ 4
Solution:
We proceed as follows:
Step I: Arrange the two given numbers as shown.
Step II: Divide 6 hundreds by 4.
|
Start by looking at the first number (hundreds place) in the dividend. Find a number in the table of 4 less than or equal to 6 We know 4 × 1 = 4. So, 1 is the required number. 4 × 1 = 4, write 1 in hundreds place of the quotient and 4 below 6. Subtract the number you got by multiplying the divisor, from the number in the dividend. Subtract 4 from 6 6 - 4 = 2 |
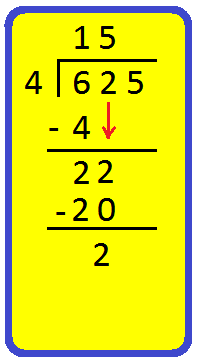
Step III:
|
Bring down the next digit (tens places), from the number in the dividend. We have 22 there; now find a number in the table of 4 that divides it. 4 × 1 = 2 4 × 2 = 8 4 × 3 = 12 4 × 4 = 16 4 × 5 = 20 So, 5 is the required number. 4 × 5 = 20, write 5 in tens place of the quotient and 20 below 22. |
Subtract the number you got by multiplying the divisor, from the number in the dividend.
Subtract 20 from 22
22 - 20 = 2
Step IV: Bring down 5
4 × 1 = 2
4 × 2 = 8
4 × 3 = 12
4 × 4 = 16
4 × 5 = 20
4 × 6 = 24
So, 6 is the required number.
4 × 6 = 24, write 6 in ones place of the quotient and 24 below 25.
Subtract the number you got by multiplying the divisor, from the number in the dividend.
Subtract 24 from 25
25 - 24 = 1.
Therefore, the quotient = 156 and remainder = 1.
Check: Dividend = Quotient × Divisor - Remainder
= 156 × 4 + 1
= 624 + 1
= 625 = Dividend
3. 645 ÷ 6
Check:
107 × 6 = 642
642 + 3 = 645
Here we know, 645 ÷ 6 = 107 remainder is 3
645 is dividend
6 is divisor
107 is quotient
3 is remainder
The same method is used when dividing larger numbers.
Word Problems on Dividing 3-Digit by 1-Digit Number:
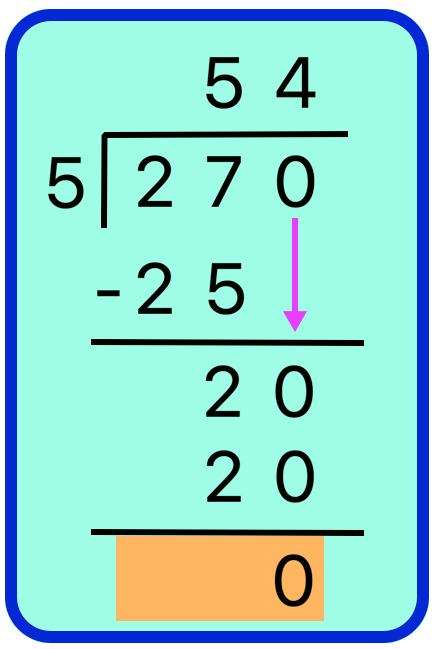
1. 270 students are to be arranged equally in 5 rows. How many students will be there in each row?
Solution:
Total number of students = 270
Number of students in each row = 270 ÷ 5
Thus, there are 54 students in each row.
Division Activity
Objective: Dividing a 3-digit number by 9 using short cut method.
Materials Required: Pen and paper only.
Procedure/Demonstration: We can divide any 3-digit number by 9 quickly.
Type 1: When the sum of the digits is less than 9.
In this case, the quotient is obtained by adding the number formed by hundreds and tens digits to the hundreds digit. The sum of the three digits gives the remainder.
213 ÷ 9, gives quotient = 21 + 2 = 23 and remainder = 2 + 1 + 3 = 6
Type 2: When the sum of the digits is greater than or equal of 9 but less than 18.
Here, we first add the number formed by hundreds and tens digits to the hundreds digit. 1 more than this sum is the quotient. To get the remainder, subtract 9 from the sum of the digits.
537 ÷ 9 gives quotient = 53 + 5 + 1 = 59 and
remainder = (9 + 8 + 7) - 9 = 15 - 9 = 6
Worksheet on Dividing 3-Digit by 1-Digit Number:
1. Find the quotient and the remainder, using long division method:
(i) 639 ÷ 3
(ii) 484 ÷ 2
(iii) 550 ÷ 5
(iv) 284 ÷ 4
(v) 504 ÷ 3
(vi) 840 ÷ 7
(vii) 248 ÷ 4
(viii) 655 ÷ 5
(ix) 616 ÷ 7
(x) 348 ÷ 4
Answer:
1. (i) Quotient: 213; Remainder: 0
(ii) Quotient: 242; Remainder: 0
(iii) Quotient: 110; Remainder: 0
(iv) Quotient: 71; Remainder: 0
(v) Quotient: 168; Remainder: 0
(vi) Quotient: 120; Remainder: 0
(vii) Quotient: 62; Remainder: 0
(viii) Quotient: 131; Remainder: 0
(ix) Quotient: 88; Remainder: 0
(x) Quotient: 87; Remainder: 0
2. Find the quotient and the remainder:
(i) 320 ÷ 6
(ii) 392 ÷ 6
(iii) 249 ÷ 7
(iv) 364 ÷ 8
(v) 193 ÷ 7
(vi) 492 ÷ 5
(vii) 524 ÷ 7
(viii) 419 ÷ 9
(ix) 270 ÷ 8
(x) 375 ÷ 7
Answer:
2. (i) Quotient: 53; Remainder: 2
(ii) Quotient: 65; Remainder: 2
(iii) Quotient: 35; Remainder: 4
(iv) Quotient: 45; Remainder: 4
(v) Quotient: 27; Remainder: 3
(vi) Quotient: 98; Remainder: 2
(vii) Quotient: 74; Remainder: 6
(viii) Quotient: 46; Remainder: 5
(ix) Quotient: 33; Remainder: 6
(x) Quotient: 53; Remainder: 4
3. Word Problems on Dividing 3-Digit by 1-Digit Number:
(i) 672 trees have to be arranged in 7 rows equally. How many trees will be in each row?
(ii) Michael bought 9 video games paying $ 648 in all. Jennifer wanted to buy only one of them. How much would she have to pay for it?
(iii) Miss Lisa asked 6 of her students to go out and collect some pebbles. They picked 186 pebbles totally. If all of them collected the same number, how many pebbles would each one have brought to the class?
(iv) Elizabeth has a 354 cm long ribbon. She wants to give it to 6 of her friends equally. What will be the length of each ribbon?
(v) A lion eats 693 kilograms of food in 9 days. If the lion is fed the same amount of food each day, how many kilograms does the lion eat per day?
(vi) Christopher has 224 blocks. How many towers of 7 blocks each can he build with them?
(vii) George has 96 stickers and he has to share these among 8 friends. How many stickers will each one get?
(viii) There are 393 oranges in a garden. They have to be packed equally in 3 baskets before sending them to the market for sale. How many fruits should be packed in each basket?
Answer:
3. (i) 96 trees
(ii) $ 72
(iii) 31 pebbles
(iv) 59 cm
(v) 77 kilograms
(vi) 32 towers
(vii) 12 stickers
(viii) 131 fruits
Related Concept
● Addition
● Check for Subtraction and Addition
● Word Problems Involving Addition and Subtraction
● Estimating Sums and Differences
● Multiply a Number by a 2-Digit Number
● Multiplication of a Number by a 3-Digit Number
● Word Problems on Multiplication
● Division of Two-Digit by a One-Digit Numbers
● Division of Four-Digit by a One-Digit Numbers
● Division by 10 and 100 and 1000
● Division by Two-Digit Numbers
From Dividing 3-Digit by 1-Digit Number to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.




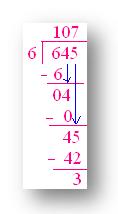


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.