Roman Symbols

Do we know from where Roman symbols came? In Rome, people wanted to use their own symbols to express various numbers. These symbols, used by Romans, are known as Roman symbols, Romans used only seven symbols V, X, L, C, D, M to express different numbers.

Roman numeric system uses seven different symbols I, V, X, L, C, D and M, which represents the values 1, 5, 10, 50, 100, 500 and 1000 of Hindu-Arabic numerals.

The Roman numeral of 2 is written as II, and for 3 it is written as III. Roman numeral for 4 is written as IV because no symbol can be repeated more than three times. There are some more rules for combining the symbols to write Roman numerals.

The Roman numeration system, developed by Romans, is based on these 7 Roman digits. 

We use these Roman digits to express different Roman numbers.

What are Roman numbers?

Roman symbols - I, V, X, L, C, D, M stand for different Roman numbers.

I stand for 1 

V stands for 5

X stands for 10

L stands for 50

C stands for 100

D stands for 500

M stands for 1000

We know in some clocks the Roman symbols marked on some of the dials of the clocks. We follow some rules to express Roman numbers.

1. We can use I and X thrice only in a numeral.

For example, we write I, II, III, for 1, 2, 3 respectively but we never write IIII for 4. We write IV for 4.

2. We never repeat V, L and D. They are used in a numeral once only.

For example, we never write VV for 10. We write X for 10.

3. When we write smaller numeral to the left of the greater numeral it means that the smaller numeral is subtracted from the greater one.

Let us consider some examples.

IV means V - I

           = 5 - 1 = 4

IX means X - I

          = 10 - 1 = 9

XL means L - X

           = 50 - 10 = 40

4. When we write a smaller numeral to the right of a greater numeral it means that the smaller numeral is added to the greater one.

VI means V + I  

           = 5 + 1 = 6  

XV means X + V

            = 10 + 5 = 6

VII  means V + II  

             = 5 + 2 = 7  

LX means L + X

           = 50 + 10 = 60

5. We never write V to the left of X. Similarly, L and D are never written to the left to any other symbol.

For example, we write XV for 15 but we never write VX for 5. We write LV for 55 but we never write LC for 50.

Rules for forming Roman Numerals:

Rule 1: Repetition of a Roman numeral means addition.

For example:

III = 1 + 1 + 1 =3

XXX = 10 + 10 + 10 = 30

Note: I, X and C can be repeated only up to three times.

Rule 2: Smaller Roman numeral to the right of a greater Roman numeral is always added to the greater numeral to give the value.

For example:

VI = 5 + 1 = 6

VII = 5 + 1 + 1 = 7

XI = 10 + 1 = 11

XII = 10 + 1 + 1 = 12

Note: Repetition of a symbol is allowed up to three times only. So, 14 is written as XIV.

Rule 3: Smaller Roman numeral to the left of a greater Roman numeral is always subtracted from the greater numeral to give the value.

For example:

IV = 5 - 1 = 4

IX = 10 - 1 = 9

Note: Repetition of a symbol on the left is not allowed. 8 cannot be written as IIX.

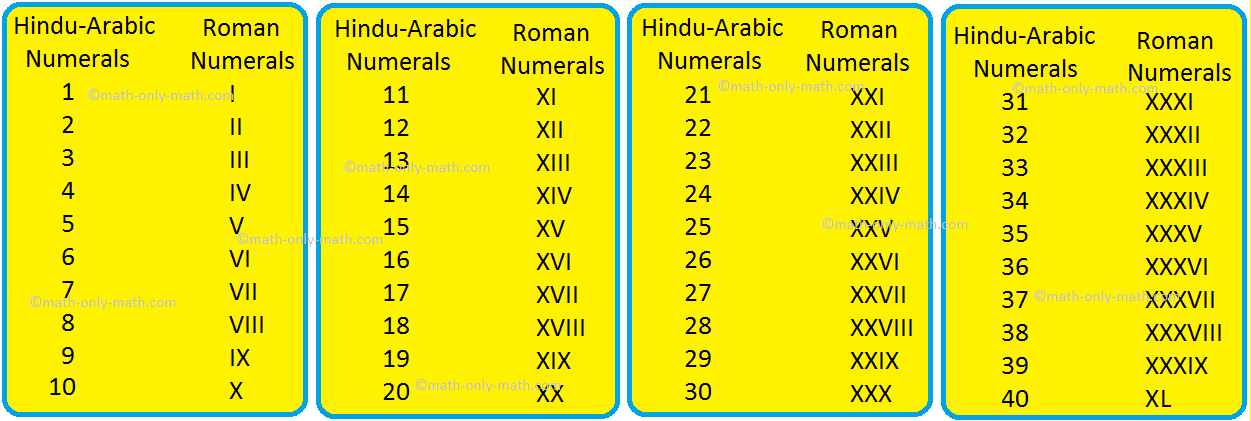
Learn the chart below showing Hindu-Arabic numerals and the corresponding Roman numerals.

There is no symbol for zero in the Roman numeric system.

In Hindu-Arabic numeration system, we use 10 symbols (digits) to write any number. These symbols are 0, 1, 2, 3, 4 1, 2, 3, 4, 5, 6, 7, 8 and 9.

Unlike the Hindu-Arabic numeration system, the Roman numeration system uses only seven symbols to write any number.

These symbols are I, V, X, L, C, D and M.

The values of these symbols are given below:

Note: There is no zero in the Roman system.

The following rules are used to write Roman numerals:

Rule I: Repetition of a Roman numeral means addition.

For example:

                    III = 1 + 1 + 1 = 3

                    XX = 10 + 10 = 20

Rule II: If a smaller Roman numeral is written to the right of a greater Roman numeral, the smaller is always added to the greater one.

For example:

                   VIII = 5 + 1 + 1 + 1 = 8

                    XII = 10 + 1 + 1 = 12

                  XXII = 10 + 10 + 1 + 1 = 22

                     XV = 10 + 5 = 15

Rule III: If a smaller Roman numeral is written to the left of a greater Roman numeral, the smaller is always subtracted from the greater one.

For example:

                   IV = 5 - 1 = 4

                   IX = 10 - 1 = 9

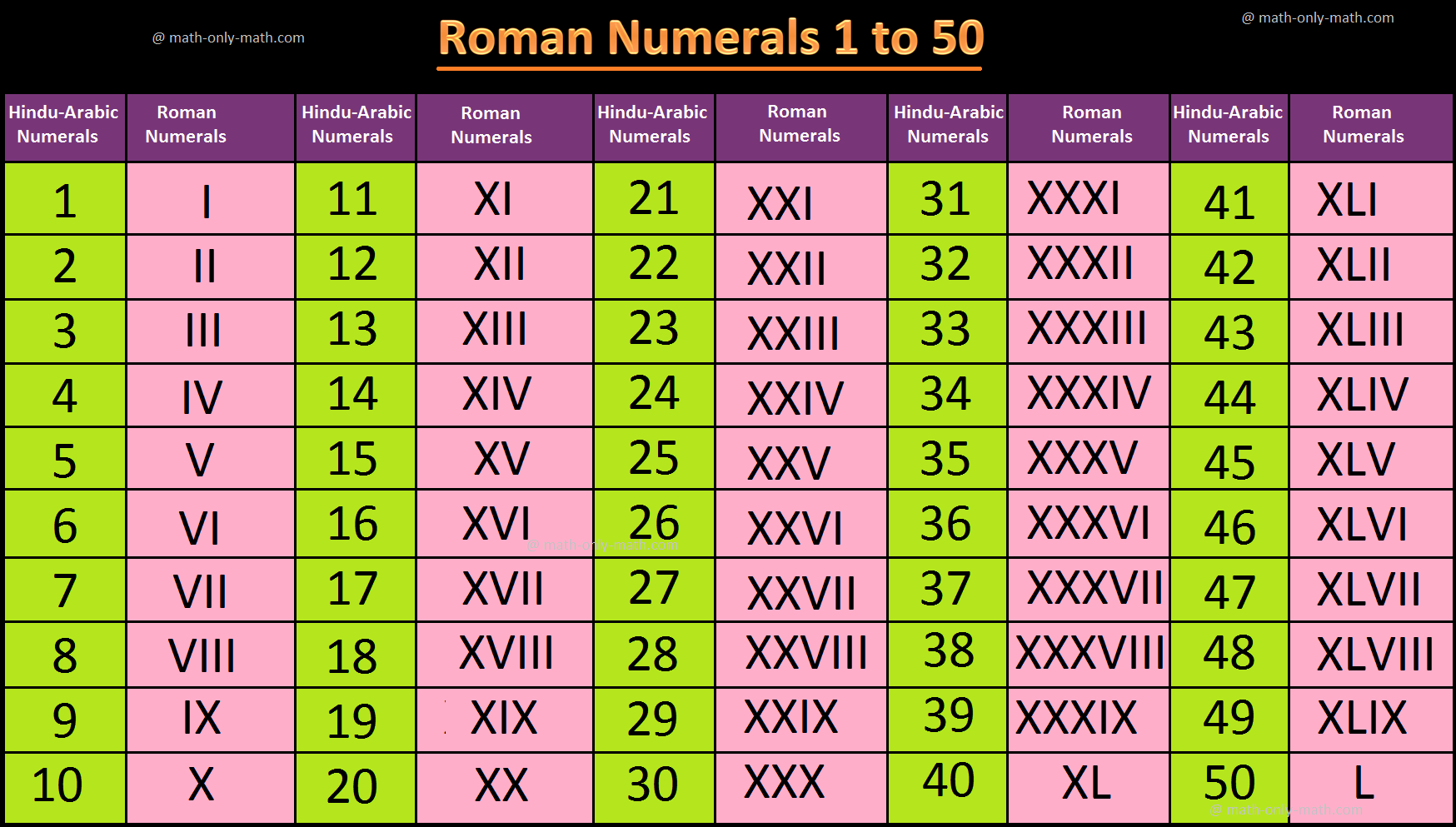
Given below is the chart showing Hindu-Arabic numerals (up to 50) and corresponding Roman numerals:

REMEMBER

In Roman numeration system,

(a) Repetition of a symbol is not allowed more than three times.

(b) The symbol V cannot be repeated or subtracted.

(c) The symbol I can be subtracted from V and X only.

4th Grade Math Activities

From Roman Symbols to HOME PAGE