Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Method of H.C.F.
We will discuss here about the method of h.c.f. (highest common factor).
Highest Common Factor (H.C.F.) or Greatest Common Divisor (G.C.D)
The highest common factor or HCF of two or more numbers is the greatest number which divides exactly the given numbers.
1. Let us consider two numbers 16 and 24.
|
Factor of 16 are → 1, 2, 4, 8, 16
Factor of 24 are → 1, 2, 3, 4, 6, 8, 12, 24 |
1 × 16, 2 × 8, 4 × 4 1 × 24, 2 × 12, 3 × 8, 4 × 6 |
We see that the highest common factor of 16 and 24 is 8. In short, the Highest Common Factor is expressed as H.C.F.
2. Find the H.C.F. of 12 and 18.
Factors of 12 = 1, 2, 3, 4, 6, 12
Factors of 18 = 1, 2, 3, 6, 9, 18
Common factors of 12 and 18 = 1, 2, 3, 6
Highest common factor (H.C.F) of 12 and 18 = 6
3. Find the H.C.F. of 15 and 28.
Factors of 15 = 1, 3, 5, 15
Factors of 28 = 1, 2, 4, 7, 14, 28
Common factors of 15 and 28 = 1
Highest common factor (H.C.F) of 15 and 28 = 1
Two numbers which have only 1 as the common factor are called co-prime.
Finding H.C.F.
There are three methods of finding H.C.F. of two or more numbers.
1. Factorization Method
2. Prime Factorization Method
3. Division Method
1. H.C.F. by Factorization Method:
Let us consider some examples.
I. Find the H.C.F. of 36 and 45.
|
Factor of 36 are → 1, 2, 3, 4, 6, 9, 12, 18, 36
Factor of 45 are → 1, 3, 5, 9, 15, 45 |
1 × 36, 2 × 18, 3 × 12, 4 × 9, 6 × 6 1 × 45, 3 × 15, 5 × 9 |
The common factors of 36 and 45 are 1, 3, 9.
The highest common factor is 9.
II. Find the HCF of 12, 48 and 72.
Let us first list all the factors of each number.
Factors of 12 are 1, 2, 3, 4, 6 and 12
Factors of 48 are 1, 2, 3, 4, 6, 8, 12, 16, 24 and 48
Factors of 72 are 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36 and 72
The common factors of 12, 48 and 7 are 1, 2, 3, 4, 6 and 12.
The highest common factor is 12.
The highest common factor of two or more numbers is the largest number that divides the given numbers exactly, without leaving a remainder.
The highest common factor of HCF is also called the greatest common divisor (GCD)
III. Find the highest common factor (HCF) of 6 and 8.
Factors of 6 → 1, 2, 3, 6
Factors of 8 → 1, 2, 4, 8
Highest common factor of 6 and 8 is 2.
IV. Find the highest common factor (HCF) of 12 and 18.
Factions of 12 → 1, 2, 3, 4, 6, 12
Factors of 18 → 1, 2, 3, 6, 9, 18
Common factors of 12 and 18 are 2, 3, 6.
Highest common factor of 12 and 18 is 6.
V. Find the H.C.F. of 25 and 45.
25 = 1 × 25
25 = 5 × 5
All the factors of 25 are 1, 5 and 25.
Also, 45 = 1 × 45
45 = 3 × 15
45 = 5 × 9
All the factors of 45 are 1, 3, 5, 9, 15 and 45.
Common factors of 25 and 45 are 1 and 5.
Thus, H.C.F. of 25 and 45 is 5.
VI. Find the H.C.F. of 18, 45 and 63.
18 = 1 × 18
18 = 2 × 9
18 = 3 × 6
All the factors of 18 are 1, 2, 3, 6, 9 and 18.
Also, 45 = 1 × 45
45 = 3 × 15
45 = 5 × 9
All the factors of 45 are 1, 3, 5, 9, 15 and 45.
Also, 63 = 1 × 63
63 = 3 × 2
63 = 7 × 9
All the factors of 63 are 1, 3, 7, 9, 21 and 63.
Common factors of 18, 45 and 63 are 1, 3 and 9.
Thus, H.C.F. of 18, 45 and 63 is 9.
REMEMBER
H.C.F. of two consecutive even numbers is 2.
2. H.C.F. by Prime Factorization Method
Let us consider an example.
I. Find the H.C.F. of 24, 36 and 48.
First we find the prime factors of 24, 36 and 48.
24 = 2 × 2 × 2 × 3
36 = 2 × 2 × 3 × 3
48 = 2 × 2 × 2 × 2 × 3
The common prime factors = 2, 2, 3
H.C.F. = 2 × 2 × 3 = 12
II. Find the H.C.F. of 132 and 330.
|
2 | 132 2 | 66 3 | 33 11 |
132 ÷ 2 = 66 66 ÷ 2 = 33 33 ÷ 3 = 11 |
|
2 | 330 5 | 165 3 | 33 11 |
330 ÷ 2 = 165 165 ÷ 5 = 33 33 ÷ 3 = 11 |
132 = 2 × 2 × 3 × 11
330 = 2 × 3 × 5 × 11
The common factors are 2, 3, 11
Therefore, H.C. F. = 2 × 3 × 11
= 66
Here 66 is also the greatest common divisor of 132 and 330.
132 ÷ 66 = 2;
330 ÷ 66 = 5
|
IV: Find the H.C.F. of 128 and 160. 128 = 2 × 2 × 2 × 2 × 2 × 2 × 2 160 = 2 × 2 × 2 × 2 × 2 × 5 The common factors are 2, 2, 2, 2, 2 H.C.F. = 2 × 2 × 2 × 2 × 2 = 32 |
2 | 128 2 | 64 2 | 32 2 | 16 2 | 8 2 | 4 2 |
2 | 160 2 | 80 2 | 40 2 | 20 2 | 10 5 |
3. H.C.F. by Division Method
To find the HCF of two or three given numbers, divide the greater number by the smaller one. Then divide the divisor by the remainder. Go on repeating the process of dividing the preceding divisor by the remainder, till zero remainder is obtained. The last divisor'is the HCF of the given numbers.
H.C.F. by Long Division Method
This method can also be used to find the H.C.F. of more than 2 numbers.
Let us consider a few examples.
1. Find the H.C.F. of 12 and 18.
|
Step I: Treat the smallest number i.e., 12 as divisor and the bigger number i.e., 18 as dividend. Step II: The remainder 6 becomes the divisor and the divisor 12 becomes the dividend. Step III: Repeat this process till the remainder becomes zero. The last divisor is the H.C.F. |
2. Find the H.C.F. of 16, 18 and 24.
|
Step I: First we consider the first two numbers and follow the same step 1, 2 and 3 of the above example. Step II: The H.C.F. of the first two numbers which is 2 becomes the divisor and the third number 24 becomes the dividend. This process is repeated till the remainder becomes 0. H.C.F. is the last divisor. |
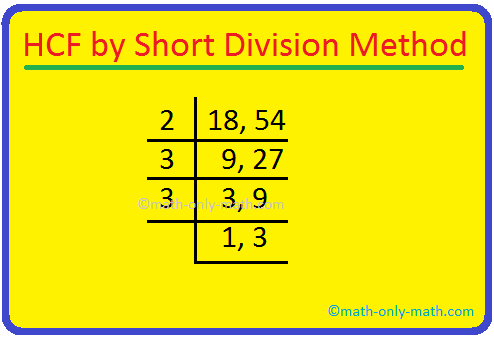
3. Find the HCF of 18 and 54 by short division method.
Solution:
Write the number in a row separated by commas, divide the numbers by common prime factors. Factorisation stops when we reach prime numbers which cannot be further divided.
HCF is the product of all the common factors.
Hence, the common factors are 2, 3 and 3.
HCF of 18 and 54 = 2 × 3 × 3 = 18.
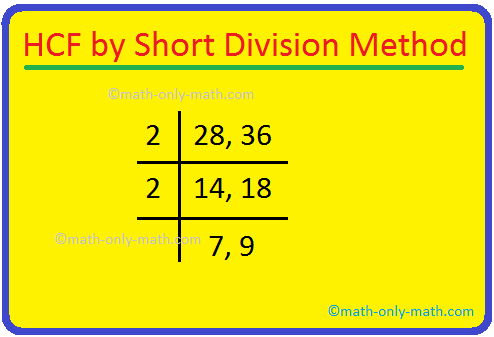
4. Find the HCF of 28 and 36 by short division method.
Solution:
First we need to write the number in a row separated by commas, divide the numbers by common prime factors. Factorisation stops when we reach prime numbers which cannot be further divided.
HCF is the product of all the common factors.
Hence, the common factors are 2, 2.
HCF of 28 and 36 = 2 × 2 = 4.
5. Find the H.C.F. of 42 and 78 by long division method.
Hence, the highest common factor of 42 and 78 is 6.
6. Find the H.C.F. of 20, 35 and 50 by long division method.
First we find the H.C.F. of any two numbers (say 20 and 35).
Since the last divisor is 5, so, 5 is the HCF of 20 and 35.
Now, we find the HCF of 5 and 50.
Hence, H.C.F. of 20, 35 and 50 is 5.
7. Find the H.C.F. of 48 and 90.
|
Steps Divide 48 and 90 by 2. 48 ÷ 2 = 24; 90 ÷ 2 = 45 Divide 24 and 45 by 3. 24 ÷ 3 = 8; 45 ÷ 3 = 15 8 and 15 do not have a common factor. Stop the division. |
Common factors are 2, 3
Therefore, H.C.F of 48 and 90 = 2 × 3 = 6
8. Find the H.C.F. of 36, 54 and 72.
|
Steps Divide 36, 54 and 72 by 2. 36 ÷ 2 = 18; 54 ÷ 2 = 27; 72 ÷ 2 = 36 Divide 18, 27 and 36 by 3. 18 ÷ 3 = 6; 27 ÷ 3 = 9; 36 ÷ 3 = 12 Divide 6, 9 and 12 by 3. 6 ÷ 3 = 2; 9 ÷ 3 = 3; 12 ÷ 3 = 4 2, 3 and 4 do not have a common factor. Stop the division. |
Common factors are 2, 3, 3
Therefore, H.C.F of 36, 54 and 72 = 2 × 3 × 3 = 18.
Worksheet on Method of H.C.F.:
I. Find the H.C.F. of the following by prime factorisation method.
(i) 44, 66
(ii) 6, 18
(iii) 675, 1125
(iv) 42, 63
(v) 81, 144
(vi) 78, 104
(vii) 64, 48
(viii) 96, 80
(ix) 24, 48
(x) 200, 400
Answer:
I. (i) 22
(ii) 6
(iii) 225
(iv) 21
(v) 9
(vi) 26
(vii) 16
(viii) 16
(ix) 24
(x) 200
II. Find the H.C.F. of the following by division method.
(i) 112, 256
(ii) 25, 65
(iii) 24, 36, 48
(iv) 7, 21, 35
(v) 30, 45, 75
(vi) 60, 75
(vii) 12, 24, 36
(viii) 90, 128, 144
(ix) 55, 88
(x) 24, 56
Answer
II. (i) 16
(ii) 5
(iii) 12
(iv) 7
(v) 15
(vi) 15
(vii) 12
(viii) 2
(ix) 11
(x) 8
III. Find the H.C.F. of the following by writing all the factors.
(i) 16, 18
(ii) 12, 36, 9
(iii) 75, 80
(iv) 6, 12, 15
(v) 20, 30, 60
Answer:
III. (i) 2
(ii) 3
(iii) 5
(iv) 3
(v) 10
From Method of Highest Common Factor to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
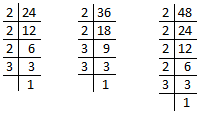
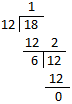
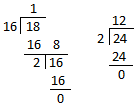
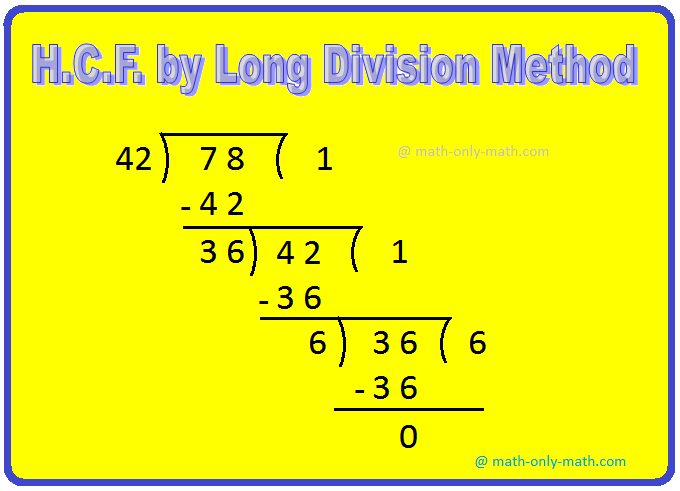

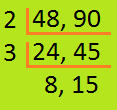



New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.