Problems on Classification of Matrices

Here we will solve different types of Problems on classification of matrices

1. Let A = \(\begin{bmatrix} -5\\3\\ 2 \end{bmatrix}\), B = \(\begin{bmatrix} 8 & 1\\ -6 & 7 \end{bmatrix}\), C = \(\begin{bmatrix} 6 & 7 & -4\\ -1 & 1 & 2\\ 3 & 0 & 5 \end{bmatrix}\),

X = \(\begin{bmatrix} 3 & 6\\ -2 & 7\\ 0 & 1 \end{bmatrix}\), Y = \(\begin{bmatrix} 8 & 0 & -4 \end{bmatrix}\).

Indicate the class of each of the matrices.

Solution:

A = \(\begin{bmatrix} -5\\3\\ 2 \end{bmatrix}\)

A is a column matrix, because it has exactly one column.

B = \(\begin{bmatrix} 8 & 1\\ -6 & 7 \end{bmatrix}\)

B is a square matrix, because number of rows = number of columns = 2

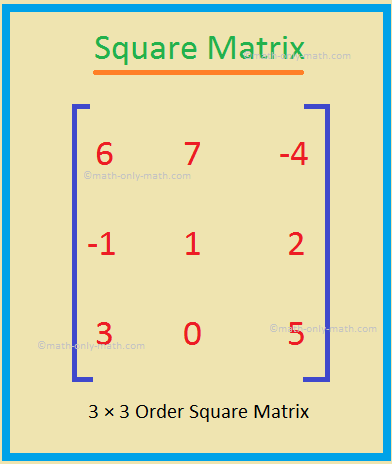
C = \(\begin{bmatrix} 6 & 7 & -4\\ -1 & 1 & 2\\ 3 & 0 & 5 \end{bmatrix}\)

C is a square matrix, because number of rows = number of columns = 3.

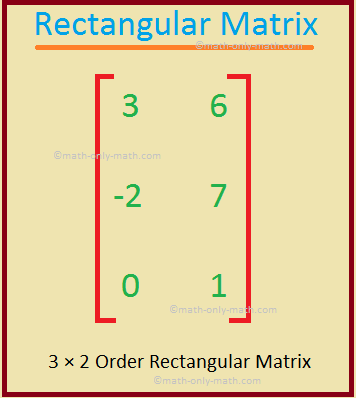
X = \(\begin{bmatrix} 3 & 6\\ -2 & 7\\ 0 & 1 \end{bmatrix}\)

X is a rectangular matrix, because number of rows ≠ number of columns.

Y = \(\begin{bmatrix} 8 & 0 & -4 \end{bmatrix}\)

Y is a row matrix, because it has exactly one row.

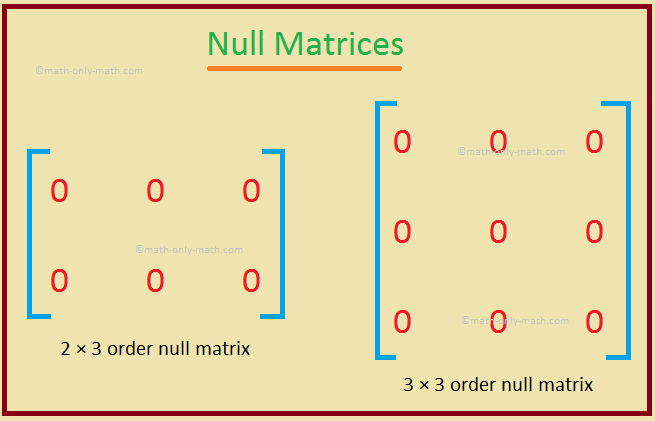
2. Construct a null matrix of the order 2 × 3 and a unit matrix of the order 3 × 3.

Solution:

A null matrix of the order 2 × 3 is \(\begin{bmatrix} 0 & 0 & 0\\ 0 & 0 & 0 \end{bmatrix}\).

A unit matrix of the order 3 × 3 is \(\begin{bmatrix} 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{bmatrix}\).

Practice Problems on Classification of Matrices:

1. let A = [8     -7     5], B = \(\begin{bmatrix} 1 & -5\\ 3 & 7 \end{bmatrix}\), C = \(\begin{bmatrix} 2 & 1 & 6\\ 1 & 0 & 5\\ 3 & 1 & 1 \end{bmatrix}\), M = \(\begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix}\) and N = \(\begin{bmatrix} 4 & -1\\ 2 & 0\\ 7 & -3 \end{bmatrix}\).

(i) Identify the rectangular matrices.

(ii) Identify the square matrices.

(iii) Identify the row matrices and the column matrices.

Answer:

(i) A and N are the rectangular matrices.

(ii) B, C and M are the square matrices.

(iii) A is the row matrix; and there is no column matrix.

2. (i) Constant the 2 × 3 zero matrix.

(ii) Constant the 4 × 4 unit matrix.

Answer:

(i) 2 × 3 order zero matrix is \(\begin{bmatrix} 0 & 0 & 0\\ 0 & 0 & 0 \end{bmatrix}\)

(ii) 4 × 4 order unit matrix is \(\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}\)

10th Grade Math

From Problems on Classification of Matrices to HOME

New! Comments

Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.

Share this page: What’s this?

FacebookXPinterestWhatsAppReddit

ShareFacebookXPinterestWhatsAppReddit