Help with Math Problems
Math Only Math is there to help with math problems from basic to intricate problems. Care has been taken to help with math problems in such a way that students can understand each and every step.
1. Simplify: 5n(2n3+n2+8)+n(4-n).Solution:
5n(2n3+n2+8)+n(4-n).
= 5n × 2n3 + 5n × n2 + 5n × 8 + n × 4 - n × n.
= 10n4 + 5n3 + 40n + 4n – n2.
= 10n4 + 5n3 + 44n – n2.
= 10n4 + 5n3 – n2 + 44n.
Answer: 10n4 + 5n3 – n2 + 44n
2. Simplify: 4y(y2-8y+6)-3(2y3-5y2+2)
Solution:
4y(y2-8y+6)-3(2y3-5y2+2).
= 4y3 - 32y2 + 24y – 6y3 + 15y2 – 6.
= 4y3 – 6y3 - 32y2 + 15y2 + 24y – 6.
= -2y3 – 17y2 + 24y – 6.
Answer: -2y3 – 17y2 + 24y – 6
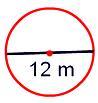
3. Find the area, diameter = 12m.
Solution:
Diameter = 12 meter.
Radius = diameter/2.
= 12/2.
= 6 meter.
Area of a circle = πr2.
Here, pi (π) = 3.14 meter, radius (r) = 6.
Area of a circle = 3.14 × 6 × 6..
= 3.14 × 36.
= 113.04 square meter or 113.04 m2.
Answer: 113.04 square meter or 113.04 m2
4. Find the area, radius = 8cm.
Solution:
Given, Radius = 8 cm.
Area of a circle = πr2.
Area of a circle = 3.14 × 8 × 8 [We know, pi (π) = 3.14].
= 3.14 × 64.
= 200.96 square cm or 200.96 cm2.
Answer: 200.96 square cm or 200.96 cm2.
5. Simplify: 4x2(x+2)+3x(5x2+2x-6)-5(3x2-4x).
Solution:
4x2(x+2) +3x(5x2+2x-6) -5(3x2-4x).
= 4x3 + 8x2 + 15x3 + 6x2 – 18x – 15x2 + 20x.
= 4x3 + 15x3 + 8x2 + 6x2 – 15x2 – 18x + 20x.
= 19x3 - x2 + 2x.
Answer: 19x3 - x2 + 2x
6. Factoring with repeated of the difference of square formula. Factor the answer completely.
3y4 – 3u4y4.
Solution:
3y4 – 3u4y4.
= 3y4(1 – u4).
= 3y4(1 – (u2)2).
= 3y4(1 + u2)( 1 - u2) [since we know a2 – b2 = (a + b)(a – b)].
= 3y4(1 + u2)( 1 + u) ( 1 - u).
Answer: 3y4(1 + u2)( 1 + u) ( 1 - u).
7. Factoring with repeated of the difference of square formula. Factor the answer completely.
u4x3 – 81x3.
Solution:
u4x3 – 81x3.
= x3(u4 – 81).
= x3((u2)2 – 92).
= x3(u2 + 9)(u2 – 9).
= x3(u2 + 9)(u2 – 32).
= x3(u2 + 9)(u + 3)(u – 3).
Answer: x3(u2 + 9)(u + 3)(u – 3).
8. Factoring with repeated of the difference of square formula. Factor the answer completely.
2w2 – 2v4w2.
Solution:
2w2 – 2v4w2.
= 2w2 (1 – v4).
= 2w2 (1 – (v2)2).
= 2w2 (1 + v2)(1 - v2).
= 2w2 (1 + v2)(1 + v)(1 – v).
Answer: 2w2 (1 + v2)(1 + v)(1 – v).
9. Factoring with repeated of the difference of square formula. Factor the answer completely.
3u2x4 – 48u2.
Solution:
3u2x4 – 48u2.
= 3u2(x4 – 16).
= 3u2((x2)2 – 42).
= 3u2(x2 +4)(x2 – 4).
= 3u2(x2 +4)(x2 – 22).
=3u2(x2 +4)(x + 2)(x – 2).
Answer: 3u2(x2 +4)(x + 2)(x – 2).
10. Factoring a sum or difference of two cubes.
Factor: 64 + u3.
Solution:
64 + u3.
= 43 + u3.
= (4 + u)(42 – 4.u + u2).
= (4 + u)(16 – 4u + u2).
Answer: (4 + u)(16 – 4u + u2)
11. Factoring a sum or difference of two cubes.
Factor: 125 - 8u3
Solution:
125 - 8u3.
= 53 – (2u)3.
= (5 – 2u)(52 + 5.2.u + (2u)2 ).
= (5 – 2u)(25 + 10u + 4u2).
Answer: (5 – 2u)(25 + 10u + 4u2)
12. Solving a linear equation with several occurrences of the variable, solve for w. Simplify your answer as much as possible.
(7w + 6)/6 + (9w +8)/2 = 22
Solution:
(7w + 6)/6 + (9w +8)/2 = 22
or, [7w + 6 + 3(9w + 8)]/6 = 22
or, 7w + 6 + 27w + 24 = 132
or, 34w + 30 = 132
or, 34w = 132 - 30
or, 34w = 102
or, w = 102/34
Therefore, w = 3
Answer: w = 3
13. Find the value of p: 2p+8p-6=7p+2p
Solution:
2p + 8p - 6 = 7p + 2p
or, 10p – 6 = 9p
or, 10p – 6 – 9p = 9p – 9p
[Subtract 9p from both the sides]
or, p – 6 = 0
or, p - 6 + 6 = 6
[Add 6 to both the sides]
Therefore, p = 6.
Answer: p = 6
14. Simplify: (24sp)/(3s)
Solution:
(24sp)/(3s).
= 8p.
Answer: 8p
15. Rewrite 3/8 as a decimal
Solution:
3/8 is a fraction; we need to change 3/8 to decimal number by dividing.
Answer: 0.375
If students have any queries in future regarding the math homework questions, please fill-up the below comment box to convey your message, so that we can help you.
● Math Questions Answers
● Help with Math Problems
● Answer Math Problems
● Math Problem Solver
● Math Unsolved Questions
● Math Questions
● Math Word Problems
● Word Problems on Speed Distance Time
● Algebra Word Problems – Money
Math Problem Answers
From Help with Math Problems to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Word Problems on Area and Perimeter | Free Worksheet with Answers
Jul 26, 24 04:58 PM
word problems on area and perimeter -
Worksheet on Perimeter | Perimeter of Squares and Rectangle | Answers
Jul 26, 24 04:37 PM
Practice the questions given in the worksheet on perimeter. The questions are based on finding the perimeter of the triangle, perimeter of the square, perimeter of rectangle and word problems. I. Find… -
Perimeter and Area of Irregular Figures | Solved Example Problems
Jul 26, 24 02:20 PM
Here we will get the ideas how to solve the problems on finding the perimeter and area of irregular figures. The figure PQRSTU is a hexagon. PS is a diagonal and QY, RO, TX and UZ are the respective d… -
Perimeter and Area of Plane Figures | Definition of Perimeter and Area
Jul 26, 24 11:50 AM
A plane figure is made of line segments or arcs of curves in a plane. It is a closed figure if the figure begins and ends at the same point. We are familiar with plane figures like squares, rectangles… -
5th Grade Math Problems | Table of Contents | Worksheets |Free Answers
Jul 26, 24 01:35 AM
In 5th grade math problems you will get all types of examples on different topics along with the solutions. Keeping in mind the mental level of child in Grade 5, every efforts has been made to introdu…
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.