Math Questions Answers

In math questions answers each questions are solved with explanation. The questions are based from different topics. Care has been taken to solve the questions in such a way that students can understand each and every step.

1. Which is greater than 4?

(a) 5,

(b) -5,

(c) -1/2,

(d) -25.


Solution:

5 greater than 4.

Answer: (a)

2. Which is the smallest?

(a) -1,

(b) -1/2,

(c) 0,

(d) 3.


Solution:

The smallest number is -1.

Answer: (a)



3. Combine terms: 12a + 26b -4b – 16a.

(a) 4a + 22b,

(b) -28a + 30b,

(c) -4a + 22b,

(d) 28a + 30b.


Solution:

12a + 26b -4b – 16a.

= 12a – 16a + 26b – 4b.

= -4a + 22b.

Answer: (c)



4. Simplify: (4 – 5) – (13 – 18 + 2).

(a) -1,

(b) –2,

(c) 1,

(d) 2.


Solution:

(4 – 5) – (13 – 18 + 2).

= -1-(13+2-18).

= -1-(15-18).

= -1-(-3).

= -1+3.

= 2.

Answer: (d)



5. What is |-26|?

(a) -26,

(b) 26,

(c) 0,

(d) 1


Solution:

|-26|

= 26.

Answer: (b)

6. Multiply: (x – 4)(x + 5)

(a) x² + 5x - 20,

(b) x² - 4x - 20,

(c) x² - x - 20,

(d) x² + x - 20.



Solution:

(x – 4)(x + 5).

= x(x + 5) -4(x + 5).

= x² + 5x – 4x – 20.

= x² + x - 20.

Answer: (d)



7. Factor: 5x² – 15x – 20.

(a) 5(x-4)(x+1),

(b) -2(x-4)(x+5),

(c) -5(x+4)(x-1),

(d) 5(x+4)(x+1).


Solution:

5x² – 15x – 20.

= 5(x² – 3x – 4).

= 5(x² – 4x + x – 4).

= 5{x(x - 4) +1(x - 4)}.

= 5(x-4)(x+1).

Answer: (a).



8. Factor: 3y(x – 3) -2(x – 3).

(a) (x – 3)(x – 3),

(b) (x – 3)²,

(c) (x – 3)(3y – 2),

(d) 3y(x – 3).

Solution:

3y(x – 3) -2(x – 3).

= (x – 3)(3y – 2).

Answer: (c).



9. Solve for x: 2x – y = (3/4)x + 6.

(a) (y + 6)/5,

(b) 4(y + 6)/5,

(c) (y + 6),

(d) 4(y - 6)/5.


Solution:

2x – y = (3/4)x + 6.

or, 2x - (3/4)x = y + 6.

or, (8x -3x)/4 = y + 6.

or, 5x/4 = y + 6.

or, 5x = 4(y + 6).

or, 5x = 4y + 24.

or, x = (4y + 24)/5.

Therefore, x = 4(y + 6)/5.

Answer: (b).

10. Simplify:(4x² - 2x) - (-5x² - 8x).


Solution:

(4x² - 2x) - (-5x² - 8x)

= 4x² - 2x + 5x² + 8x.

= 4x² + 5x² - 2x + 8x.

= 9x² + 6x.

= 3x(3x + 2).



Answer: 3x(3x + 2)

11. Find the value of 3 + 2 • (8 – 3)

(a) 25,

(b) 13,

(c) 17,

(d) 24,

(e) 15.


Solution:

3 + 2 • (8 – 3)

= 3 + 2 (5)

= 3 + 2 × 5

= 3 + 10

= 13

Answer: (d)

12. Rice weighing 3³/₄ pounds was divided equally and placed in 4 containers. How many ounces of rice were in each?


Solution:

3³/₄ ÷ 4 pounds.

= (4 × 3 + 3)/4 ÷ 4 pounds.

= 15/4 ÷ 4 pounds.

= 15/4 × 1/4 pounds.

= 15/16 pounds.

Now we know that, 1 pound = 16 ounces.

Therefore, 15/16 pounds = 15/16 × 16 ounces.

= 15 ounces.

Answer: 15 ounces.



13. Factor: 16w³ – u⁴w³


Solution:

16w³ – u⁴w³.

= w³(16 – u⁴).

= w³(4² - ((u²)²).

= w³(4 + u²)(4 - u²).

= w³(4 + u²)(2² - u²).

= w³(4 + u²)(2 + u)(2 - u).

Answer: w³(4 + u²)(2 + u)(2 - u).



14. Factor: 3x⁴y³ – 48y³.


Solution:

3x⁴y³– 48y³.

= 3y³(x⁴ – 16).

= 3y³[(x²)² - 4²].

= 3y³(x² + 4)(x² - 4).

= 3y³(x² + 4)(x² - 2²).

= 3y³(x² + 4)(x + 2)(x -2).

Answer: 3y³(x² + 4)(x + 2)(x -2)

15. What is the radius of a circle that has a circumference of 3.14 meters?


Solution:

Circumference of a circle = 2πr.

Given, circumference = 3.14 meters.

Therefore,

2πr = Circumference of a circle

or, 2πr = 3.14.

or, 2 × 3.14r = 3.14,[Putting the value of pi (π) = 3.14].

or, 6.28r = 3.14.

or, r = 3.14/6.28.

or, r = 0.5.

Answer: 0.5 meter.

16. The trip from Carville to Planesborough takes 4$\frac{1}{2}$ hours when travelling at a constant speed of 70 miles per hour. How long, in hours, does the trip take when travelling at a constant speed of 60 miles per hour.

Solution:

Distance = Speed × Time

Distance form Carville to Planesborough = 70 × 4$\frac{1}{2}$ miles

                                                        = 70 × $\frac{9}{2}$ miles

                                                            = 315 miles

Now travelling the same distance (315 miles) at a constant speed of 60 miles per hour.

Time = $\frac{Distance}{Speed}$

         = $\frac{315}{60}$ hours

        = 5.25 hours

Time taken to travel Carville to Planesborough a constant speed of 60 miles per hour = 5.25 hours.

17. The table below shows the number of hours Simon worked this week at his job. Days: Hours: Monday 6 2/3. Tuesday 4 1/2. Thursday 7 1/4. He earns $12 an hour at his job. How much will Simon get paid for the hours he worked this week?

Solution:

Total hours Simon worked this week = 6 2/3 + 4 1/2 + 7 1/4

                                                     = $\frac{20}{3}$ + $\frac{9}{2}$ + $\frac{29}{4}$ hours

                                                     = $\frac{80}{12}$ + $\frac{54}{12}$ + $\frac{87}{12}$ hours

                                                     = $\frac{80 + 54 + 87}{12}$ hours

                                                     = $\frac{221}{12}$ hours
He earns $12 an hour at his job.

Simon get paid for the hours he worked this week = $ $\frac{221}{12}$ × 12 = $ 221

18. Carlos is looking to buy a house where the floor plan shows the ratio of the area of the living room to the kitchen to the bedroom is 5 : 3 : 4. If the combined area of those three rooms is 360 square feet, how much larger, in square feet, is the living room than the bedroom?

Answer:

The area of the living room = $\frac{5}{5 + 3 + 4}$ × 360 square feet

                                        = $\frac{5}{12}$ × 360 square feet

                                        = 5 × 30 square feet

                                        = 150 square feet

The area of the bed room = $\frac{4}{5 + 3 + 4}$ × 360 square feet

                                        = $\frac{4}{12}$ × 360 square feet

                                        = 4 × 30 square feet

                                        = 120 square feet

Therefore, living room is (150 - 120) square feet = 30 square feet larger than the bed room.

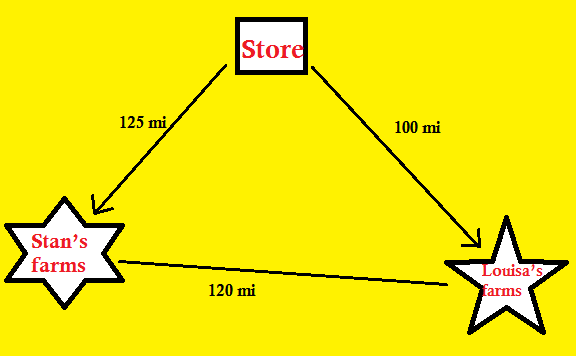
19. Frank runs a business called Frank’s Fresh Farm Produce. Once a week he drives to farms where he buys the best possible fresh produce for his customers. Frank can travel 600 miles on a full tank of gas. Usually Frank has time to visit only one farm on each trip, but one week he decides to visit both Stan’s and Louisa’s farms.

● When Frank drives from his store to Stan’s farm and back, he knows he uses 5/12 of a tank

● When Frank drives to Louisa’s farm and back, he uses 1/3 of a tank.

From a map of the area, he learns that there is a road from Stan’s farm to Louisa’s farm that is 120 miles long. He realizes that he can drive from his store to Stan’s farm, then to Louisa’s farm, and then back to his store on a loop. Frank can tell by looking at his fuel gauge that he has 5/8 of a tank of gas. Can he drive this loop without having to stop for fuel? Or should he buy gas before he starts his trip?

Solution:

Frank drives from his store to Stan’s farm and back, he knows he uses 5/12 of a tank

Frank can travel 600 miles on a full tank of gas.

So, for 5/12 tank of gas he can travel = 600 × 5/12 = 50 × 5 = 250 mi

Therefore, the distance from store to Stan’s farms = 250/2 mi = 125 mi

Similarly, when Frank drives to Louisa’s farm and back, he uses 1/3 of a tank.

So, for 1/3 tank of gas tank he can travel = 600 × 1/3 = 200 × 1 = 200 mi

Therefore, the distance from store to Stan’s farms = 200/2 mi = 100 mi

Distance from Stan’s farm to Louisa’s farm is 120 mi.

Loop distance = Store to Stan’s farm to Louisa’s farm to Store

                     = 125 mi + 120 mi + 100 mi 

                     = 345 mi 

Therefore, Loop distance = 345 mi

Frank can tell by looking at his fuel gauge that he has 5/8 of a tank of gas.

So, for 5/8 tank of gas tank he can travel = 600 × 5/8 = 75 × 5 = 375 mi

Therefore, 5/8 tank of gas tank Frank can travel = 375 mi

345 mi < 375 mi

Thus, Frank drive this loop without having to stop for fuel.

20. A moving company charges a $200 fee, plus $4 for every item that is delivered safely. The moving company takes $5 off the bill for every item that is lost or broken.

A florist hired this moving company to move 578 clay pots. The moving company lost 6 pots, broke 12 pots, and delivered the rest of the pots safely. How much did the florist pay the moving company?

A. $2,350

B. $2,440

C. $2,442

D. $2,512

Answer: 

A. $2,350

The company lost 6 pots and broke 12 pots.

Total number of lost and broken pots = 6 + 12 = 18

Company takes $5 off the bill for every item that is lost or broken.

The company takes 18 × 5 = $ 90 off the bill for 18 lost and broken pots.

Florist hired this company to move 578 clay pots.

We know, total number of lost and broken pots = 18

Therefore, total number of safely delivered pots = (578 - 18) pots = 560 pots.

Company charges a flat fee of $200, plus $4 for every item that is delivered safely.

So, for 560 pots the company charges $200 + $(560 × 4) = $200 + $2240 = $2440.

We know, the company takes $90 off the bill for 18 lost and broken pots.

Therefore, the florist paid $2440 - $90 = $2350 to the moving company.

21. Charlie and Augustus guessed the weight of a bar of chocolate and decided the person whose guess was closest would get to eat it. Charlie guessed 35 grams, Augustus guessed 40 grams, and the actual weight was 37.5 grams. Augustus says he should get the chocolate bar and showed this work below. Do you agree with Augustus? Explain below with mathematical and written reasoning.

22. Two out of three balls in a Multi-colored package are pink. How many balls in a package of 21 will be pink?

Solution:

Let the x out of 21 balls are pink.

2 out of 3 balls in a Multi-colored package are pink.

x : 2 = 3 : 21

x/2 = 21/3

3x = 2 × 21

3x = 42

x = 42/3 = 14

Answer: There are 14 pink balls.

23. Carmen wants to buy a snack that costs $3.74 including tax. Carmen gives the cashier $10. Which equation can be used to find the amount of change, x, that Carmen receives? How much change did she receive?

(a) x + 3.74 = 10; Carmen receives $6.26 in change.

(b) x + 10 = 3.74; Carmen receives $13.74 in change.

(c) x - 3.74 = 10; Carmen receives $13.74 in change.

(d) x - 10 = 3.74; Carmen receives $6.26 in change.

Answer: 

(a) x + 3.74 = 10; Carmen receives $6.26 in change.

24. Melissa earns $5 an hour for babysitting. If she babysat for 7 hours on Saturday and 6 hours on Sunday, how much money did she make in total?

Solution:

Melissa earns $5 an hour for babysitting.

Total work hours on Saturday and Sunday = (7 + 6) hours = 13 hours

She earn = $ 5 × 13 = $ 65

Answer: $ 65

More Math Questions Answers:

25. Kiran and Clare live 24 miles away from each other along a trail. One Saturday the two friends statred walking towards each other along the trail at 8:00 am with a plan ot have a picnic when they met. Kiran walks at a speed of 3 miles per hour while Clrare walks 3.4 miles per hour. after one hour, how far apart will they be?

Solution:

Kiran and Clare live 24 miles away from each other along a trail.

Kiran walks at a speed of 3 miles per hour

In 1 hour Kiran covered 3 miles

Clrare walks 3.4 miles per hour.

In 1 hour Clrare covered 3.4 miles

In 1 hour both Kiran and Clrare covered = (3 + 3.4) miles= 6.4 miles.

(They statred walking towards each other along the trail, so we add the distance)

After one hour they will be (24 - 6.4) miles = 17.6 miles apart.

Answer: 17.6 miles

26. 8/9 kilogram of berries is added to a container that already has $\frac{7}{3}$ kilograms of berries. After this, the container is $\frac{2}{3}$ of the way full. How many kilograms of berries can this container hold?

Solution:

$\frac{8}{9}$kilogram of berries is added to a container that already has 7/3 kilograms of berries.

$\frac{8}{9}$ + $\frac{7}{3}$ = $\frac{24}{27}$ + $\frac{63}{27}$ = $\frac{87}{27}$ = $\frac{29}{9}$ kilograms

$\frac{2}{3}$ of the way full = $\frac{29}{9}$ kilograms

Container hold = $\frac{29}{9}$ ÷ $\frac{2}{3}$ kilograms 

                      = $\frac{29}{9}$ × $\frac{3}{2}$ kilograms 

                      = $\frac{87}{18}$ kilograms 

                      = $\frac{29}{6}$ kilograms 

                      = 4$\frac{5}{6}$ kilograms 

Answer: 4$\frac{5}{6}$ kg

27. Shylah is picking out a rectangular aquarium for her new fish. The height of aquarium A is half the height of aquarium B. The length of aquarium B is twice the length of aquarium A. The widths of the two aquariums are the same.

Shylah wants to buy the aquarium with the greater amount of room for her fish to swim.

Which aquarium should she buy? Explain your reasoning.

Solution:

The height of aquarium A is half the height of aquarium B.

Let the height of aquarium B = H 

The height of aquarium A = H/2

The length of aquarium B is twice the length of aquarium A.

Let the length of aquarium A = L

The length of aquarium B = 2L

The widths of the two aquariums are the same.

Let widths of the two aquariums = W

Volume of aquarium A = Length × Width × Height

                                 = L × W × H/2

                                 = 1/2 (L × W × H)

Volume of aquarium B = Length × Width × Height

                                 = 2L × W × H

                                 = 2 (L × W × H)

Volume of aquarium B > Volume of aquarium A

Shylah should buy Aquarium B

Answer: Aquarium B

28. At a bus station, buses begin their routes at 6:00 a.m. The schedule for two of the buses is based on the time intervals listed below.

Bus A has a long route and leaves the station every 75 minutes.

Bus B has a short route and leaves the station every 15 minutes.

What is the next time Bus A and Bus B will leave the bus station at the same time?

Solution:

The LCM (least common multiple) of 75 and 15 is 75.

Now add 75 minutes to 6:00 a.m.

75 minutes = 1 hour 15 minutes

6:00 a.m. + 1 hour 15 minutes = 7:15 a.m.

At 7:15 a.m. bus A and bus B will leave the bus station at the same time.

29. After Winter Break, 6 musicians joined the drama club so the number of actors in the club was equal to the number of musicians in the club. How many more musicians need to join the club to make the ratio of actors to musicians 3 to 5?

A. 6 musicians

B. 9 musicians

C. 10 musicians

D. 16 musicians

Solution:

At the start of the school year,

Let the number of members = x

Actors : Musicians = 5 : 3

Number of actors = $\frac{5}{8}$x and number of musicians = $\frac{3}{8}$x

After Winter Break, 6 musicians joined the drama club.

Number of musicians after winter break = $\frac{3}{8}$x + 6

The number of actors in the club was equal to the number of musicians in the club.

According to the problem, 

$\frac{5}{8}$x = $\frac{3}{8}$x + 6

$\frac{5}{8}$x - $\frac{3}{8}$x = 6

$\frac{2}{8}$x = 6

x = 6 × $\frac{8}{2}$

x = $\frac{48}{2}$

x = 24

At the start of the school year, the number of members = 24

Number of actors = $\frac{5}{8}$ × 24 = 15

Number of musicians = $\frac{3}{8}$ × 24 = 9

After Winter Break, 6 musicians joined the drama club.

Number of actors = Number of musicians = 15

Let y number of musicians need to join the club to make the ratio of actors to musicians 3 to 5

Therefore,

15 : (15 + y) = 3 : 5

$\frac{15}{15 + y}$ = $\frac{3}{5}$

3 × (15 + y) = 15 × 5

45 + 3y = 75

3y = 75 - 45

3y = 30

y = $\frac{30}{3}$

y = 10

Thus, 10 number of musicians need to join the club to make the ratio of actors to musicians 3 to 5

Answer: 

C. 10 musicians

30. LaRon is shelving books in a library. He has 36 mysteries, 27 biographies, and 45 historical fiction books. LaRon wants to put the same number of books on each shelf, and he will only put books of the same genre on the same shelf.

What is the smallest possible number of shelves LaRon would need to store these books in this way?

Solution:

Mysteries = 36

Biographies = 27

Historical = 45

Now find the factors of 36, 27 and 45

The factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18 and 36.

The factors of 27 = 1, 3, 9, and 27.

Factors of 45 = 1, 3, 5, 9, 15 and 45.

The highest common factor of 36, 27 and 45 is 9.

Hence, the minimum number of book in each shelf = 9

Answer: 9

31. Jayden spends 1$\frac{1}{12}$ hours at each soccer practice and 1$\frac{8}{30}$ hours at each basketball practice. If he has two soccer practices each week and two basketball practices each week how many total hours does he have sports practice each week?

Solution:

Jayden spends 1$\frac{1}{12}$ hours at each soccer practice.

Time required for two soccer practices = 1$\frac{1}{12}$ + 1$\frac{1}{12}$ hours

                                                        = $\frac{13}{12}$ + $\frac{13}{12}$ hours

                                                        = $\frac{26}{12}$ hours

                                                       = $\frac{13}{6}$ hours

                                                       = 2 $\frac{1}{6}$ hours

Jayden spends 1$\frac{8}{30}$ hours at each basketball practice.

Time required for two basketball practices = 1$\frac{8}{30}$ + 1$\frac{8}{30}$ hours

                                                             = $\frac{38}{30}$ + $\frac{38}{30}$ hours

                                                             = $\frac{76}{30}$ hours

                                                             = $\frac{38}{15}$ hours

                                                             = 2 $\frac{8}{15}$ hours

Required time = 2$\frac{1}{6}$ hours + 2$\frac{8}{15}$ hours

                     = ($\frac{13}{6}$ + $\frac{38}{15}$) hours

                     = ($\frac{65}{30}$ + $\frac{76}{15}$) hours

                     = ($\frac{141}{30}$) hours

                     = 4($\frac{21}{30}$) hours

Answer: 4 21/30 hours

32. A recipe for cookies requires 16 cups of sugar. A recipe for brownies requires 2 pints of sugar. You have 4 quarts of sugar.

Are you able to make both recipes, and if so, do you have any sugar left over?

Solution:

A recipe for cookies requires 16 cups of sugar.

A recipe for brownies requires 2 pints of sugar.

2 pints = 4 cups

16 cups + 4 cups = 20 cups required to make both recipes.

You have 4 quarts of sugar.

4 quarts = 16 cups of sugar.

i.e, You have only 16 cups of sugar.

Answer:  No; You won't be able to make both recipes.

33. Michael deposited $3569 on Tuesday, withdrew $1556 on Wednesday and again on Thursday, he deposited $532 in the bank. How much money did Michael have in his account in the bank?

Solution:

Total deposited amounts on Tuesday and Thursday = $3569 + $532

                                                                          = $4101

Withdrew amount on Wednesday = $1556

Therefore, Michael have in his account in the bank =  $4101 - $1556

                                                                         = $ 2545

Answer: $ 2545

34. Christopher goes to the market with $800. He buys a blackboard for $135, a pair of boots for $99 and stationery for $356. How much money is left with Christopher?

Solution:

Cost of a blackboard = $135

Cost of pair of boots = $99

Stationery = $356

The total amount Christopher spent = $135 + $99 + $356

                                                     = $590

Therefore, the money is left with Christopher = $800 - $590

                                                                                                                                                                           = $210

Answer: $210

35. Find the difference between the greatest and the smallest numbers that can be formed using the digits 6,2,7,4,3, each only once.

Solution:

The greatest numbers formed using the digits 6,2,7,4,3 is 76,432

The smallest numbers formed using the digits 6,2,7,4,3 is 23,467

Difference between the greatest and the smallest numbers = 76,432 - 23,467 = 52,965

Answer: 52,965

36. A vessel has 4 ℓ 500 mℓ of curd. In how many glasses, each of 25 mℓ capacity, can it be filled?

Solution:

Capacity of a vessel = 4 ℓ 500 mℓ 

Each glass contains 25 mℓ 

Now divide 4 ℓ 500 mℓ by 25 mℓ 

4 ℓ 500 mℓ = 4 ℓ + 500 mℓ = 4000 mℓ 500 mℓ = 4500 mℓ

4 ℓ 500 mℓ ÷ 25 mℓ

= 4500 mℓ ÷ 25 mℓ

= 180

Answer: 180 glasses

37. Ron travels 13 km 500 m in an hour and consumes 1ℓ of petrol for every 6 km.

(i) How much distance will he travel in 8 hours?

(ii) How much petrol will he required to travel?

Solution:

(i) Distance covered by Ron in 1 hour = 13 km 500 m

Distance covered in 8 hours = 13 km 500 m × 8

                                         = 108 km

(ii) Total distance = 108 km

Consumes 1ℓ petrol to cover = 6 km

Therefore, to cover 108 km it consumes = (108 ÷ 6) ℓ = 18ℓ

Answer: 

5. (i) 108 km

(ii) 18 ℓ

38. The New York Times newspaper is published everyday. One copy of newspaper has 15 pages. Everyday 12,790 copies are printed for all. How many pages are printed everyday?

Answer: 191,850 Pages

39. Multiple Choice Questions (MCQ)

Choose the correct option.

(i) Population of Texas in 2013 was 34,269,123. It increased by 6,298,313 in the next four years, but 1,942,639 migrated to New York. The population of Texas in 2017 was

(a) 38,624,797

(b) 40,567,436

(c) 27,970,810

(d) 36,211,762

(ii) A factory produces 8960 bulbs in one day and after 2 weeks, these bulbs are distributed equally to seven retailers in different parts of the city. How many bulbs does each dealer get?

(a) 27,895

(b) 17,920

(c) 10,256

(d) 8,695

(iii) If Nairitee multiplies 280 by 25 instead of 24, the difference in product is

(a) 280

(b) 170

(c) 28

(d) 380

Answer: 

39. (i) (a) 3,86,24,797

(ii) (b) 17,920

(iii) (a) 280

40. I am a three-digit number. I am less than 700. I am greater than 400. All my digits are odd. If you take each of my three digits and add them together, they equal 7. What number am I?

Solution: 

The number is less than 700 and and greater than 400.

All the numbers are odd.

We can take any numbers between 500 to 599.

Sum of the all three digits = 7

We we take hundred place is 5 then the sum of the tens palce and ones place = (7 - 5) = 2

Sum of two odd numbers = 2 i.e, 1 and 1

Then number will be 511.

Therefore, the required number is 511.

Answer: 511.

41. Find the number, if the number is multiple of 9, the number is an odd number, the number is greater than the number of days in July, the number is less than 65, and the sum of the digit is equal to 2 more than the number of days in a week.

Solution:

Number of days in July = 31

The number is greater than the number of days in July, the number is less than 65 and the number is multiple of 9 are 36, 45, 54, 63.

The number is an odd number

Odd numbers are 45 and 63

The sum of the digit of the number is equal to 2 more than the number of days in a week.

i.e., 7 + 2 = 9

Thus, sum of the digits = 9

We can clearly see that odd numbers and the sum of the digits = 9 is 63.

Since, 6 + 3 = 9

Therefore, the required number is 63.

Answer: 63

42. I am a six-digit number. I have a 4 in my hundred thousands place, a 3 in my ten thousands place, and a 2 in my thousands place. I am a palindrome. (A palindrome reads the same, forwards and backwards. The words "pop" and "level" are palindromes. The numbers '353' and '956659' are palindromes.) What number am I?

Solution:

A six digit number with a 4 in hundred thousands place, a 3 in my ten thousands place, and a 2 in my thousands place and palindrome

The number is 432234.

The required number is 432234.

Answer: 432234.

43. The New York Times newspaper is published everyday. One copy of newspaper contains 20 pages and a total of 107200 pages are printed everyday. How many copies are printed everyday?

Solution:

Total number of pages printed everyday = 107200.

Total number of pages in one copy = 20

Total number of copies printed everyday = 107200 ÷ 20 = 5360

Answer: 5360

44. Find the product of the greatest number of 7-digits and the smallest number of 8-digits.

Solution:

Greatest number of 7-digits = 9,999,999

Smallest number of 8-digits = 10,000,000

Product = 9999999 × 10000000 = 99,999,990,000,000.

Answer: 99,999,990,000,000.

45. A swimming pool is 224 m long and 126 m wide. How much distance will Nairitee cover in going 10 times around it?

Solution:

Perimeter of the swimming pool = 2(length + width)

                                               = 2(224 + 126) m

                                               = 2 (350) m

                                               = 700 m

Distance covered by Nairitee around the swimming pool 10 times = (700 × 10) m = 7000 m = 7 km

Answer: 7 km

46. A bus consumed 40 litres of diesel in going from Dumdum to Sealdah and another 50 litres of diesel in going from Sealdah to Howrah. If the diesel cost $275 per litre, find the total amount spent on diesel.

Solution:

Quantity of diesel consumed to cover from Dumdum to Sealdah = 40 litres 

Quantity of diesel consumed to cover from Sealdah to Howrah = 50 litres

Therefore, total quantity of diesel consumed = 40 litres + 50 litres

                                                                 = 90 litres

Cost of 1 litre diesel = $275

Quantity of diesel = 90 litres

Therefore, cost of 90 litres of diesel = $(275 × 90)

                                                    = $24,750

Answer: $24,750

47. A dealer buys 50 tables and 50 chairs. If a table costs $1,129 and a chair costs $874, find the total money spent by him.

Cost of 50 tables = $(1,129 × 50) 

Cost of 50 chair = $(874 × 50)

Cost of 50 tables and 50 chairs = $(1,129 × 50) + $(874 × 50)

                                             = $50(1,129 + 874)

                                             = $50(2,003)

                                             = $100,150

Answer: $100,150

48. Find the product of the greatest number of 8-digits and the greatest number of 2-digits.

Solution:

The greatest 8-digit number = 99,999,999

The greatest 2-digit number = 99

Therefore, the required product = 99,999,999 × 99

                                              = 9,899,999,901

49. A motorcycle moves at a uniform speed of 94 km/h. How much distance will it cover in 67 hours?

Solution: 

Motorcycle uniform speed of 94 km/h

Distance covered in 67 hours = (94 × 67) km

                                           = 6298 km

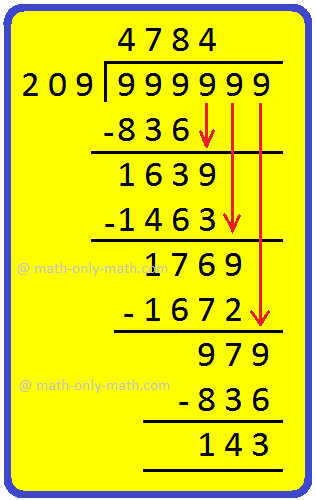
50. Find the largest 6-digit number which is exactly divisible by 209.

Solution:

The largest 6-digit number = 999,999

The required number = 999,999 - 143 = 999,856.

Answer: 999,856.

51. Find the greatest 7-digit number exactly divisible by 81.

Solution:

The largest 6-digit number = 9,999,999

9,999,999 = 123,456 × 81 + 63

The required number = 9,999,999 - 63 = 9,999,936

Answer: 9,999,936

52. What least number should be added to the 87956 so that the sum is exactly divisible by 31?

Solution:

87956 ÷ 31 = 2837 × 2837 + 9

Quotient = 2837

Remainder = 9

Least number to be added = 31 - 9 = 22

Check: 87956 + 22 = 87978

87978 ÷ 31 = 2838

Answer: 22

53. Multiple Choice Questions (MCQ) on Math Questions Answers:

     Tick (✔) the correct option.

(i) The LCM of 204, 120 and 102 is

(a) 4803

(b) 540

(c) 2040

(d) 4123

(ii) If the LCM of 48, 76 is 912, their HCF is

(a) 4

(b) 8

(c) 5

(d) 0

(iii) The HCF of two numbers is 117 and their LCM is 4680. If one of the numbers is 936. the other one is

(a) 234

(b) 462

(c) 672

(d) 585

Answer: 

53. (i) The LCM of 204, 120 and 102 is (c) 2040.

(ii) If the LCM of 48, 76 is 912, their HCF is (a) 4.

(iii) The HCF of two numbers is 117 and their LCM is 4680. If one of the numbers is 936. the other one is (d) 585.

54. Jenna uses up 24% of the gas in her car on her way to school. If she uses 0.96 gallons of gas on her way to school, how much gas did she have in her car before she left?

Solution:

0.96/24%

= 0.96/0.24

= 4

Jenna had 4 gallons of gas before her trip.

55. Mr Chehab was driving home from work when he hit traffic. It took him 4/5 an hour to travel two miles. What was Mr. Chehab's speed during that time?

Solution:

In $\frac{4}{5}$ an hour Mr Chehab travelled two miles.

In 1 hour Mr Chehab travelled 2 ÷ $\frac{4}{5}$ miles.

                                         = 2 × $\frac{5}{4}$ miles.

                                         = $\frac{10}{4}$ miles.

                                         = $\frac{5}{2}$ miles.

                                         = 2$\frac{1}{2}$ miles.

Mr. Chehab's speed during that time was 2$\frac{1}{2}$ miles/hour.

56. Use the ratio of shoes to pants from the chart.

Calculate how many pairs of shoes this person has if he has 32 pants.

Solution:

Number of shoes = 2

Number of pants = 8

Ratio of shoes to pants = $\frac{\textrm{Number of shoes}}{\textrm{Number of pants}}$

                                 = $\frac{2}{8}$

Let the required number of pairs of shoes = x

Number of pants given = 32

 $\frac{2}{8}$ =  $\frac{x}{32}$

⟹ 8x = 2 × 32

⟹ 8x = 64

⟹ x = $\frac{64}{8}$

⟹ x = 8

Therefore, the required answer is 8 pairs of shoes.

Math Questions Answers

57. A superhero team has 15 heroes. 6 of them can fly, and the rest have super strength. What is the ratio of superheroes who can fly to those who have super strength?

Solution:

A superhero team has 15 heroes.

Number of superheroes who can fly = 6

Number of superheroes who have super strength = 15 - 6 = 9

Now, the ratio of superheroes who can fly to those who have super strength = 6 : 9

             = 2 : 3

Answer: 2 : 3

If students have any queries regarding the questions given in the math questions answers, please fill-up the below comment box to convey your message, so that we can help you.

● Math Questions Answers
● Help with Math Problems
● Answer Math Problems
● Math Problem Solver
● Math Unsolved Questions
● Math Questions
● Math Word Problems
● Word Problems on Speed Distance Time
● Algebra Word Problems – Money

Math Problem Answers Index

From Math Questions Answers to HOME PAGE