Word Problems on Subtraction

In word problems on subtraction we need to read the question carefully and understand what we need to find out.

We know, in subtraction the larger number from which we subtract the other number (the smaller number) is called minuend, the number (the smaller number) which is subtracted is called subtrahend and the result of subtraction is called the difference.

So, we need to write the statement and then find the difference between two numbers, i.e. subtract the smaller number from the bigger number.

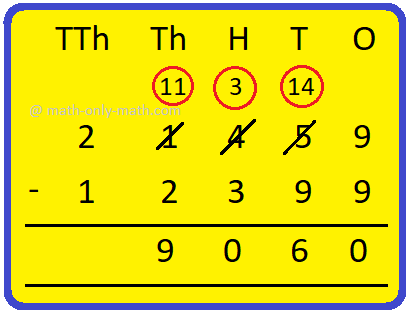
1. A factory produced 12,399 scooters in 2012. In 2013, it produced 21,459 scooters. By how much did the production of the factory increase?

Solution: Production in 2013 = 21,459 Production in 2012 = 12,399 Increase in production = 21,459 - 12,399                                  = 9,060

Hence, the production increased by 9,060

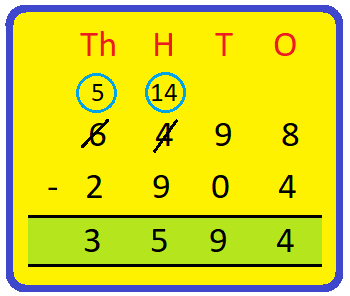
2. What must be added to 2,904 to get 6,498?

Solution: The sum of two numbers = 6,498 One number = 2,904 The other number 6,498 - 2,904 = 3,594 Hence, the required number = 3,594

3. Anthony collected 4825 coins and his friend Bryan collected 1935 coins. How many more coins did Anthony collect compare to Bryan?

Solution:

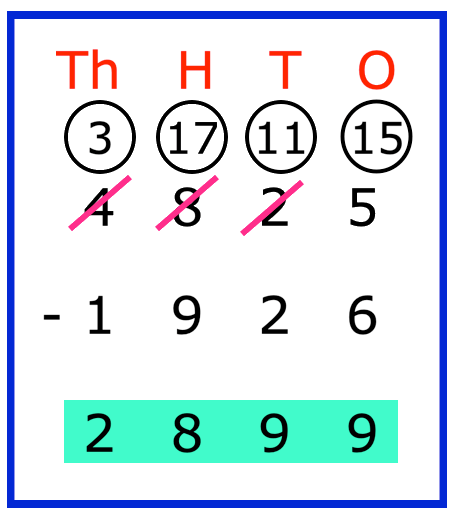
4. There were 4825 passengers in a train. 1926 got down at a station. How many passengers were left in the train?

Total number of passengers = 4825 Number of passengers got down = 1926 Passengers left in the train = 4825 - 1926                                         = 2899

Thus, 2899 passengers were left in the train.

Worksheet on Word problems on Subtraction:

1. The population of a town is 9,123. If the number of males is 3,572, find the number of females in the town.

2. In an examination, 8,380 candidates appeared. Out of these, 4,090 candidates failed. How many candidates passed?

3. A factory produced 8,540 bulbs in the year 2014. Out of them 3,479 bulbs were found defective. How many bulbs were found good?

4. By how much is 21,998 greater than 36,994.

5. What must be added to 4,488 to get 6,409?

6. What must be added to 2,680 to get 7,498?

7. The sum of two numbers is 14,892. If one of them is 7,892, find the other

8. The difference between two numbers is 6,452. If the greater number is 9,294 find the smaller number.

9. A factory produced 13,285 TV sets in April and 20,302 TV sets in May. Find the increase in the number of TV sets.

10. 43,742 persons came to see a football match on Sunday. 27,936 persons came on Monday. How many more persons visited on Sunday? Write the number sentence.

11. Deepika bought a motorcycle for ₹40,000 and a scooter for ₹28560, How much did she pay more for the motorcycle?

15. The population of a town is 82,010. If 43,413 are men, 25,929 are women and the remaining are children, find the number of children.

16. Michael bought 504 eggs and sold 349 of them. How many eggs are left with Michael?

17. There were 3459 students in The Heritage School. 2433 of them are boys. How many girls are there in the school?

18. A cartoon box contains white and pink balls. If the total number of balls is 1200 and 890 of these are white, how many pink balls are there in the cartoon box?

19. David has 469 marbles with him and Linda has 603 marbles with her. Who has more marbles and how many?

20. In a sanctuary, there are 8401 monkeys. 2005 monkeys were transferred to another sanctuary. How many monkeys are left in the first sanctuary?

21. Christopher bought 5680 packets of noodles. He sold 3409 packets. How many noodle packets are left with Christopher?

22. In a college, there are 7810 students. If 3569 are boys, then find the numbers of girls.

23. A wrist watch costs $ 59. If you give $ 100 note to the shopkeeper, how much money will you get back?

24. In a confectionery store, there were 3468 chicken pastries. If, only 2085 chicken pastries could be sold, find the number of chicken pastries left.

Answer:

1. 5551

2. 4290

3. 5061

4. 14996

5. 1921

6. 4818

7. 7000

8. 2842

9. 7017

10. 15806

11. 11440

15. 12668

16. 155 eggs

17. 1026 girls

18. 310 pink balls

19. Linda; 134 marbles

20. 6396 monkeys

21. 2271 packets of noodles

22. 4241 girls

23. $ 41

24. 1383 chicken pastries

4th Grade Math Activities

From Subtraction with Regrouping to HOME PAGE