Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Fraction as Division
Fraction as division is also known as fraction as quotient.
Can you divide a smaller number by a bigger number?
We have learnt how to divide a bigger number by a smaller number.
We know that 12 ÷ 4 = 3.
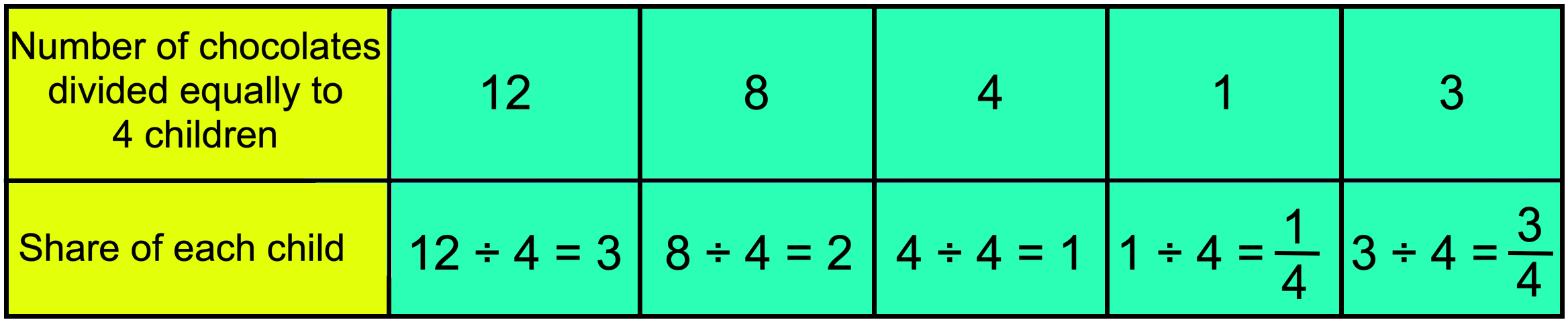
If you have 12 chocolates and these are distributed equally to 4 children, then each one gets 3 chocolates. If 8 chocolates are distributed to 4 children, the share of each one is 2 chocolates, because 842. When we equally distribute 4 chocolates to 4 children, then each one gets 1 chocolate.
What do you observe from this? The number of children is the same, but the number of chocolates is decreasing. Also, when the number of chocolates is decreasing, then the share for each one is decreasing.

Let us consider the following situation, where there is only 1 chocolate and it is to be distributed equally among 4 children.
The chocolate can be divided into 4 equal parts and 1 part can be given to each child.

Here, no child is getting 1 whole chocolate, rather each one is only getting a part of the 1 whole chocolate. The share of each one is \(\frac{1}{4}\), as there are four equal parts and each one is getting one part.
\(\frac{1}{4}\) is the result obtained when 1 is divided by 4.
Let us consider the another situation, in which there are 3 chocolates in a packet and these chocolates are to be distributed equally to 4 children.
This can be done in the following way:
1. Divide each of the three chocolates into 4 equal parts.
2. Count the total numbers of parts (pieces) obtained, here 12 parts.
3. Divide these 12 parts among 4 children equally.
4. Each child gets 3 parts after division, i.e., 3 parts out of 4 of a chocolate. In other words, each child gets 3/4 of a chocolate.
Now, the above description is represented in a tabular form as follows:
Now, we can say that it is possible to divide a smaller number by a bigger number. The result in these cases is not a whole number, it is only a part of a whole or a fraction.
So, \(\frac{1}{4}\) is the same as 1 ÷ 4,
\(\frac{3}{4}\) is the same as 3 ÷ 4.
Examples on Fraction as division
If 8 biscuits are distributed between 2 children equally, then each of them will get 8 ÷ 2 = 4 biscuits.
If 4 biscuits are distributed between 2 children equally, then each of them will get 4 ÷ 2 = 2 biscuits.
If 1 biscuit is to be shared between 2 children equally, then each one of them will get 1/2 (1 ÷ 2) biscuits.
Similarly,
If 5 apples are distributed between 2 children equally, then each one will get 5 ÷ 2 or 5/2 apples.
For examples the divisions can be expressed as fractions.
(i) 8 ÷ 2 = 8/2;
(ii) 12 ÷ 4 = 12/4
(iii) 5 ÷ 3 = 5/3
(iv) 15 ÷ 5 = 15/5
(v) 11 ÷ 19 = 11/19
(vi) If Sufi has 3 cookies and she wants to give equal share to Rachel, what share both will get? We divide 3 by 2. It is written as fraction \(\frac{3}{2}\).
1. For examples the fractions can be expressed as division.
(i) 9/7 = 9 ÷ 7
(ii) 3/11 = 3 ÷ 11
(iii) 90/63 = 90 ÷ 63
(iv) 1/5 = 1 ÷ 5
(v) 14/17 = 14 ÷ 17
2. Express each of the following fractions as division:
(i) \(\frac{1}{7}\)
(ii) \(\frac{3}{8}\)
(iii) \(\frac{11}{15}\)
Solution:
(i) \(\frac{1}{7}\) = 1 ÷ 7
(ii) \(\frac{3}{8}\) = 3 ÷ 8
(iii) \(\frac{11}{15}\) = 11 ÷ 15
● Fraction
- Representations of Fractions on a Number Line
- Fraction as Division
- Types of Fractions
- Conversion of Mixed Fractions into Improper Fractions
- Conversion of Improper Fractions into Mixed Fractions
- Equivalent Fractions
- Interesting Fact about Equivalent Fractions
- Fractions in Lowest Terms
- Like and Unlike Fractions
- Comparing Like Fractions
- Comparing Unlike Fractions
- Addition and Subtraction of Like Fractions
- Addition and Subtraction of Unlike Fractions
- Inserting a Fraction between Two Given Fractions
From Fraction as Division to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.






New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.