Comparing Unlike Fractions

In comparing unlike fractions, we first convert them into like fractions by using the following steps and then compare them.

Step I:

Obtain the denominators of the fractions and find their LCM (least common multiple).


Step II:

Each fractions are converted to its equivalent fraction with denominator equal to the LCM (least common multiple) obtained in Step I.

Step III:

Compare the numerators of the equivalent fractions whose denominators are same.

Solved Examples on Comparing Unlike Fractions:

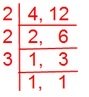
1. Which is larger \(\frac{3}{4}\) or \(\frac{5}{12}\)?

Solution:

Let us first find the LCM (least common multiple) of the denominators 4 and 12.

We have,

Therefore, LCM (least common multiple) of 4 and 12 is 2 × 2 × 3 = 12.

Now we convert the given fractions to equivalent fractions with denominator 12

We have,

\(\frac{3}{4}\) = \(\frac{3 × 3}{4 × 3}\) = \(\frac{9}{12}\)

\(\frac{5}{12}\) = \(\frac{5 × 1}{12 × 1}\) = \(\frac{5}{12}\)

Now we will observe the numerator, that is 9 > 5.

So, \(\frac{9}{12}\) > \(\frac{5}{12}\)

Therefore, \(\frac{3}{4}\) > \(\frac{5}{12}\).



2. Compare \(\frac{7}{8}\) and \(\frac{5}{6}\).

Solution:

First we find the LCM of denominators .

We have,

Therefore, LCM (least common multiple) = 2 × 2 × 2 × 3 = 24.

Now, we convert each fraction into equivalent fraction with 24 as its denominator.

We have,

\(\frac{7}{8}\) = \(\frac{7 × 3}{8 × 3}\) = \(\frac{21}{24}\); [since, 24 ÷ 8 = 3]

\(\frac{5}{6}\) = \(\frac{5 × 4}{6 × 4}\) = \(\frac{20}{24}\); [since 24 ÷ 6 = 4]

Now we will observe the numerator, that is 20 < 21

So, \(\frac{20}{24}\) < \(\frac{21}{24}\)

Therefore, \(\frac{5}{6}\) < \(\frac{7}{8}\).

3. Arrange the fractions \(\frac{5}{8}\), \(\frac{5}{6}\), \(\frac{7}{4}\), \(\frac{3}{5}\) in ascending order.

Solution:

Let us first find the LCM (least common multiple) of the denominators:

We have,

Therefore, LCM (least common multiple) = 2 × 2 × 2 × 3 × 5 = 120. Now, we convert each fraction into equivalent fraction with 120 as its denominator.

We have,

\(\frac{5}{8}\) = \(\frac{5 × 15}{8 × 15}\) = \(\frac{75}{120}\), [since 120 ÷ 8 = 15].

\(\frac{5}{6}\) = \(\frac{5 × 20}{6 × 20}\) = \(\frac{100}{120}\), [since 120 ÷ 6 = 20].

\(\frac{7}{4}\) = \(\frac{7 × 30}{4 × 30}\) = \(\frac{210}{120}\), [since 120 ÷ 4 = 30].

\(\frac{3}{5}\) = \(\frac{3 × 24}{5 × 24}\) = \(\frac{72}{120}\), [since 120 ÷ 5 = 24].

Now we will observe the numerator, that is 72 < 75 < 100 < 210.

So, \(\frac{72}{120}\) < \(\frac{75}{120}\) < \(\frac{100}{120}\) < \(\frac{210}{120}\).

Therefore, \(\frac{3}{5}\), \(\frac{5}{8}\), \(\frac{5}{6}\), \(\frac{7}{4}\).



4. Arrange the following fractions in descending order \(\frac{3}{8}\), \(\frac{5}{6}\), \(\frac{2}{4}\), \(\frac{1}{3}\), \(\frac{6}{8}\).

Solution:

We observe that the given fractions neither have common denominator nor common numerator.

So, first we convert them into like fractions i.e. fractions having common denominator. For this, we first find the LCM (least common multiple) of the denominators of the given fractions.

Denominators are 8, 6, 4, 3, 8.

We have,

Therefore, LCM (least common multiple) = 2 × 2 × 2 × 3 = 24.

Now, we convert each fraction into equivalent fraction with 24 as its denominator.

Thus,

\(\frac{3}{8}\) = \(\frac{3 × 3}{8 × 3}\) = \(\frac{9}{24}\); [since 24 ÷ 8 = 3]

\(\frac{5}{6}\) = \(\frac{5 × 4}{6 × 4}\) = \(\frac{20}{24}\) ; [since 24 ÷ 6 = 4]

\(\frac{2}{4}\)= \(\frac{2 × 6}{4 × 6}\) = \(\frac{12}{24}\) ; [since 24 ÷ 4 = 6]

\(\frac{1}{3}\)= \(\frac{1 × 8}{3 × 8}\) = \(\frac{8}{24}\) ; [since 24 ÷ 3 = 8]

\(\frac{6}{8}\) = \(\frac{6 × 3}{8 × 3}\) = \(\frac{18}{24}\) ; [since 24 ÷ 8 = 3]

Now we will observe the numerator, that is 20 > 18 > 12 > 9 > 8.

So, \(\frac{20}{24}\) > \(\frac{18}{24}\) > \(\frac{12}{24}\)  > \(\frac{9}{24}\) > \(\frac{8}{24}\) .

Therefore, \(\frac{5}{6}\) > \(\frac{6}{8}\) > \(\frac{2}{4}\) > \(\frac{3}{8}\) > \(\frac{1}{3}\) 

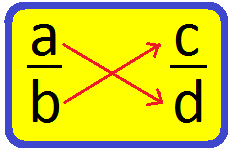
Cross Multiplication Method of Comparing Two Unlike Fractions:

Let \(\frac{a}{b}\) and \(\frac{c}{d}\) be the two given fractions. To compare these fractions, we cross multiply: as shown:

Then, we find the cross products ad and bc.

(i) ad > bc then \(\frac{a}{b}\) > \(\frac{c}{d}\)

(ii) ad < bc then \(\frac{a}{b}\) < \(\frac{c}{d}\)

(iii) If ad = bc then \(\frac{a}{b}\) = \(\frac{c}{d}\)

1. Compare \(\frac{2}{8}\) and \(\frac{3}{5}\)

Solution:

We can compare the given fractions by cross multiplication method easily.

2 × 5 = 10 and 3 × 8 = 24

Therefore, 2 × 5 < 3 × 8

i.e., \(\frac{2}{8}\) < \(\frac{3}{5}\)

We can also compare the given fractions by converting them to like fractions.

The LCM of denominators 8 and 5 is 40.

Therefore, we convert \(\frac{2}{8}\) and \(\frac{3}{5}\) into like fractions each having denominator 40.

\(\frac{2}{8}\) = \(\frac{2 × 5}{8 × 5}\) = \(\frac{10}{40}\) and \(\frac{3}{5}\) = \(\frac{3 × 8}{5 × 8}\) = \(\frac{24}{40}\)

Now \(\frac{10}{40}\) and \(\frac{24}{40}\) are like fractions.

Clearly, 10 < 24.

Therefore, \(\frac{10}{40}\) < \(\frac{24}{40}\),

i.e., \(\frac{2}{8}\) < \(\frac{3}{5}\).

To compare two unlike fractions, we first convert them to like fractions.

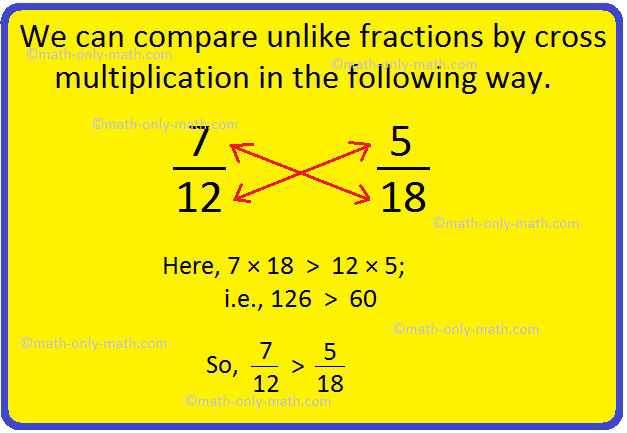
1. Compare \(\frac{7}{12}\) and \(\frac{5}{18}\).

Solution:

Let us first convert both fractions to like fractions and then compare.

LCM of denominators 12 and 18 is 36.

Divide 36 by 12, we get 3. Now, multiply both numerators and denominator of the fraction \(\frac{7}{12}\) by 3.

\(\frac{7 × 3}{12 × 3}\) = \(\frac{21}{36}\)

Divide 36 by denominator of the second fraction. i.e. 18, we get 2.

Multiply numerator and denominator of the fraction \(\frac{5}{18}\) by 2.

\(\frac{5 × 2}{18 × 2}\) = \(\frac{10}{36}\)

Compare the two fractions \(\frac{21}{36}\) and \(\frac{10}{36}\). Here 21 > 10. Thus, \(\frac{7}{12}\) > \(\frac{5}{18}\).

Alternate Method:

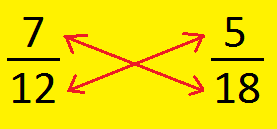
We can compare unlike fractions by cross multiplication in the following way.

Here, 7 × 18 > 12 × 5; 126 > 60

So, \(\frac{7}{12}\) > \(\frac{5}{18}\)

2. Arrange the following fractions in ascending order \(\frac{1}{4}\), \(\frac{3}{2}\), \(\frac{7}{8}\), \(\frac{1}{16}\)

Solution: LCM of denominators 4, 2, 8 and 16 = 16

Here, the given fractions can be written as

\(\frac{1}{4}\) = \(\frac{1 × 4}{4 × 4}\) = \(\frac{4}{16}\)

\(\frac{3}{2}\) = \(\frac{3 × 8}{2 × 8}\) = \(\frac{24}{16}\)

\(\frac{7}{8}\) = \(\frac{7 × 2}{8 × 2}\) = \(\frac{14}{16}\)

\(\frac{1}{16}\) = \(\frac{1 × 1}{16 × 1}\) = \(\frac{1}{16}\)

Ascending order is \(\frac{1}{16}\) < \(\frac{4}{16}\) < \(\frac{14}{16}\) < \(\frac{24}{16}\)

                        or, \(\frac{1}{16}\) < \(\frac{1}{4}\) < \(\frac{7}{8}\) < \(\frac{3}{2}\)

Questions and Answers on Comparing Unlike Fractions:

1. Compare the given fractions by putting the right sign <, > or =.

(i) \(\frac{1}{5}\) ___ \(\frac{1}{11}\)

(ii) \(\frac{7}{6}\) ___ \(\frac{4}{6}\)

(iii) \(\frac{3}{18}\) ___ \(\frac{3}{15}\)

(iv) \(\frac{2}{3}\) ___ \(\frac{3}{4}\)

(v) \(\frac{6}{12}\) ___ \(\frac{8}{16}\)

(vi) \(\frac{5}{5}\) ___ \(\frac{5}{7}\)

(vii) \(\frac{5}{6}\) ___ \(\frac{12}{18}\)

(viii) \(\frac{10}{15}\) ___ \(\frac{14}{21}\)

(ix) \(\frac{2}{7}\) ___ \(\frac{5}{13}\)

Answers:

(i) >

(ii) >

(iii) <

(iv) <

(v) =

(vi) >

(vii) >

(viii) =

(ix) <

2. Arrange the given fractions in ascending order.

(i) \(\frac{3}{6}\), \(\frac{3}{8}\), \(\frac{3}{4}\)

(ii) \(\frac{1}{16}\), \(\frac{1}{4}\), \(\frac{1}{2}\)

(iii) \(\frac{1}{2}\), \(\frac{3}{4}\), \(\frac{5}{8}\)

(iv) \(\frac{2}{5}\), \(\frac{3}{4}\), \(\frac{3}{5}\)

Answers:

(i) \(\frac{3}{8}\), \(\frac{3}{6}\), \(\frac{3}{4}\)

(ii) \(\frac{1}{16}\), \(\frac{1}{4}\), \(\frac{1}{2}\)

(iii) \(\frac{1}{2}\), \(\frac{5}{8}\), \(\frac{3}{4}\)

(iv) \(\frac{2}{5}\), \(\frac{3}{5}\), \(\frac{3}{4}\)

Word Problems on Comparing Unlike Fractions:

3. Robert ate \(\frac{9}{22}\) part of the pizza and Maria ate \(\frac{5}{11}\) part of the pizza. Who ate the greater part of the pizza? What fraction of pizza was finished by the two girls?

Solution:

Robert ate \(\frac{9}{22}\) part of the pizza.

Maria ate \(\frac{5}{11}\) part of the pizza.

Let us first convert both fractions to like fractions and then compare.

Let us find the LCM of the denominators 22 and 11. 

The LCM of 22 and 11 is 22.

\(\frac{9}{22}\) = \(\frac{9 × 1}{22 × 1}\) = \(\frac{9}{22}\)

\(\frac{5}{11}\) = \(\frac{5 × 2}{11 × 2}\) = \(\frac{10}{22}\)

Compare the two fractions \(\frac{9}{22}\) and \(\frac{10}{22}\).

Here 10 > 9. Thus, \(\frac{5}{11}\) > \(\frac{9}{22}\).

Maria ate the greater part of the pizza.

Now add the two fractions\(\frac{9}{22}\) + \(\frac{5}{11}\)

We get the like fractions \(\frac{9}{22}\) and \(\frac{5}{22}\).

Now, \(\frac{9}{22}\) + \(\frac{10}{22}\)       

= \(\frac{9 + 10}{22}\)       

= \(\frac{19}{22}\)

Therefore, \(\frac{19}{22}\) of the pizza was finished by the two girls?

3. Ron covered a distance of \(\frac{5}{6}\) km and Jon covered a distance of \(\frac{3}{4}\) km. Who covered the greater distance?

Answer: Ron 

4. Adrian cycled for \(\frac{62}{8}\) km and Steven cycled \(\frac{27}{4}\) km during the weekend. Who cycled more and by how much?

Answer: Adrian, 1 km 

● Fraction

• Representations of Fractions on a Number Line
• Fraction as Division
• Types of Fractions
• Conversion of Mixed Fractions into Improper Fractions
• Conversion of Improper Fractions into Mixed Fractions
• Equivalent Fractions
• Interesting Fact about Equivalent Fractions
• Fractions in Lowest Terms
• Like and Unlike Fractions
• Comparing Like Fractions
• Comparing Unlike Fractions
• Addition and Subtraction of Like Fractions
• Addition and Subtraction of Unlike Fractions
• Inserting a Fraction between Two Given Fractions

Numbers Page

6th Grade Page

From Comparing Unlike Fractions to HOME PAGE