Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Word Problems on Fraction
In word problems on fraction we will solve different types of problems on multiplication of fractional numbers and division of fractional numbers.
I. Word Problems on Addition of Fractions:
1. Nairitee took \(\frac{7}{8}\) hour to paint a table and \(\frac{2}{3}\) hour to paint a chair. How much time did he take in painting both items?
Solution:
Total time taken in painting both items = \(\frac{7}{8}\) h + \(\frac{2}{3}\) h
= (\(\frac{7}{8}\) + \(\frac{2}{3}\)) h
= (\(\frac{21 + 16}{24}\)) h
= \(\frac{37}{24}\) h
= 1\(\frac{13}{24}\) h
Therefore, Nairitee took 1\(\frac{13}{24}\) hours in painting both items.
2. Nitheeya and Nairitee \(\frac{3}{10}\) and \(\frac{1}{6}\) of a cake respectively. What portion of the cake did they eat together?
Solution:
The portion of cake ate by Nitheeya = \(\frac{3}{10}\)
The portion of cake ate by Nitheeya = \(\frac{1}{6}\)
The portion they ate together = \(\frac{3}{10}\) + \(\frac{1}{6}\)
= \(\frac{9}{30}\) + \(\frac{5}{30}\); [Since, LCM of 10 and 6 = 30]
= \(\frac{9 + 5}{30}\)
= \(\frac{14}{30}\)
= \(\frac{7}{15}\)
Therefore, together Nitheeya and Nairitee ate \(\frac{7}{15}\) of the cake.
3. Rachel took \(\frac{1}{2}\) hour to paint a table and \(\frac{1}{3}\) hour to paint a chair. How much time did she take in all?
Solution:
|
Time taken to paint a table = \(\frac{1}{2}\) hour Time taken to paint a chair = \(\frac{1}{3}\) hour Total time taken = \(\frac{1}{2}\) hour + \(\frac{1}{3}\) hour = \(\frac{5}{6}\) hour |
\(\frac{1}{2}\) + \(\frac{1}{3}\) L.C.M. of 2, 3 is 6. = \(\frac{3}{6}\) + \(\frac{2}{6}\) \(\frac{1 × 3}{2 × 3}\) = \(\frac{3}{6}\) \(\frac{1 × 2}{3 × 2}\) = \(\frac{2}{6}\) |
II. Word Problems on Subtraction of Fractions:
1. Out of \(\frac{12}{17}\) m of cloth given to a tailor, \(\frac{1}{5}\) m were used. Find the length of cloth unused.
Solution:
Length of the cloth given to the tailors = \(\frac{12}{17}\) m
Length of cloth used = \(\frac{1}{5}\) m
Length of the unused cloth = \(\frac{12}{17}\) m - \(\frac{1}{5}\) m
= (\(\frac{12}{17}\) - \(\frac{1}{5}\)) m
= (\(\frac{12 × 5}{17 × 5}\) - \(\frac{1 × 17}{5 × 17}\)) m; [Since, LCM of 17 and 5 = 85]
= (\(\frac{60}{85}\) - \(\frac{17}{85}\)) m
= (\(\frac{60 - 17}{85}\) m
= (\(\frac{43}{85}\) m
2. Nairitee has $6\(\frac{4}{7}\). She gives $4\(\frac{2}{3}\) to her mother. How much money does she have now?
Solution:
Money with Nairitee = $6\(\frac{4}{7}\)
Money given to her mother = $4\(\frac{2}{3}\)
Money left with Nairitee = $6\(\frac{4}{7}\) - $4\(\frac{2}{3}\)
= $(6\(\frac{4}{7}\) - 4\(\frac{2}{3}\))
= $(\(\frac{46}{7}\) - \(\frac{14}{3}\))
= $(\(\frac{46 × 3}{7 × 3}\) - \(\frac{14 × 7}{3 × 7}\)); [Since, LCM of 7 and 3 = 21]
= $(\(\frac{138}{21}\) - \(\frac{98}{21}\))
= $\(\frac{40}{21}\)
= $1\(\frac{19}{21}\)
Therefore, Nairitee has $1\(\frac{19}{21}\).
3. If 3\(\frac{1}{2}\) m of wire is cut from a piece of 10 m long wire, how much of wire is left?
Total length of the wire = 10 m
Fraction of the wire cut out = 3\(\frac{1}{2}\) m = \(\frac{7}{2}\) m
Length of the wire left = 10 m – 3\(\frac{1}{2}\) m
= [\(\frac{10}{1}\) - \(\frac{7}{2}\)] m, [L.C.M. of 1, 2 is 2]
= [\(\frac{20}{2}\) - \(\frac{7}{2}\)] m, [\(\frac{10}{1}\) × \(\frac{2}{2}\)]
= [\(\frac{20 - 7}{2}\)] m
= \(\frac{13}{2}\) m
= 6\(\frac{1}{2}\) m
III. Word Problems on Multiplication of Fractions:
1. \(\frac{4}{7}\) of a number is 84. Find the number.
Solution:
According to the problem,
\(\frac{4}{7}\) of a number = 84
Number = 84 × \(\frac{7}{4}\)
[Here we need to multiply 84 by the reciprocal of \(\frac{4}{7}\)]
= 21 × 7
= 147
Therefore, the number is 147.
2. One half of the students in a school are girls, \(\frac{3}{5}\) of these girls are studying in lower classes. What fraction of girls are studying in lower classes?
Solution:
Fraction of girls studying in school = \(\frac{1}{2}\)
Fraction of girls studying in lower classes = \(\frac{3}{5}\) of \(\frac{1}{2}\)
= \(\frac{3}{5}\) × \(\frac{1}{2}\)
= \(\frac{3 × 1}{5 × 2}\)
= \(\frac{3}{10}\)
Therefore, \(\frac{3}{10}\) of girls studying in lower classes.
3. Maddy reads three-fifth of 75 pages of his lesson. How many more pages he need to complete the lesson?
Solution:
Maddy reads = \(\frac{3}{5}\) of 75
= \(\frac{3}{5}\) × 75
= 45 pages.
Maddy has to read = 75 – 45.
= 30 pages.
Therefore, Maddy has to read 30 more pages.
4. Nitheeya walks 2\(\frac{1}{2}\) km distance in one hour. How many kilometres can she walk in 8\(\frac{1}{4}\) hours?
Solution:
Distance walk in 1 hour = 2\(\frac{1}{2}\)
Distance can be walked in 8\(\frac{1}{4}\) hours
= 8\(\frac{1}{4}\) * 2\(\frac{1}{2}\) km
= \(\frac{8 × 4 + 1}{4}\) * \(\frac{2 × 2 + 1}{2}\)
= \(\frac{33}{4}\) * \(\frac{5}{2}\)
= \(\frac{33 × 5}{4 × 2}\)
= \(\frac{165}{8}\)
= 20\(\frac{5}{8}\) km
IV. Word Problems on Division of Fractions:
1. A herd of cows gives 4 litres of milk each day. But each cow gives one-third of total milk each day. They give 24 litres milk in six days. How many cows are there in the herd?
Solution:
A herd of cows gives 4 litres of milk each day.
Each cow gives one-third of total milk each day = \(\frac{1}{3}\) of 4
Therefore, each cow gives \(\frac{4}{3}\) of milk each day.
Total no. of cows = 4 ÷ \(\frac{4}{3}\)
= 4 × \(\frac{3}{4}\)
= 3
Therefore there are 3 cows in the herd.
Worksheet on Word problems on Fractions:
1. Shelly walked \(\frac{1}{3}\) km. Kelly walked \(\frac{4}{15}\) km. Who walked farther? How much farther did one walk than the other?
2. A frog took three jumps. The first jump was \(\frac{2}{3}\) m long, the second was \(\frac{5}{6}\) m long and the third was \(\frac{1}{3}\) m long. How far did the frog jump in all?
3. A vessel contains 1\(\frac{1}{2}\) l of milk. John drinks \(\frac{1}{4}\) l of milk; Joe drinks \(\frac{1}{2}\) l of milk. How much of milk is left in the vessel?
4. Between 4\(\frac{2}{3}\)and 3\(\frac{2}{3}\) which is greater and by how much?
5. What must be subtracted from 5\(\frac{1}{6}\) to get 2\(\frac{1}{8}\)?
● Multiplication is Repeated Addition.
● Multiplication of Fractional Number by a Whole Number.
● Multiplication of a Fraction by Fraction.
● Properties of Multiplication of Fractional Numbers.
● Worksheet on Multiplication on Fraction.
● Division of a Fraction by a Whole Number.
● Division of a Fractional Number.
● Division of a Whole Number by a Fraction.
● Properties of Fractional Division.
● Worksheet on Division of Fractions.
● Simplification of Fractions.
● Worksheet on Simplification of Fractions.
● Worksheet on Word Problems on Fractions.
From Word Problems on Fraction to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
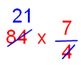
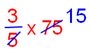
![To convert a percentage into a fraction, place the given number over 100 and reduce it to its lowest term. Consider the following example: (i) 20% [We know % = 1/100]](/image-thumbnails/convert-a-percentage-into-a-fraction.png/default.webp)











New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.