Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Equivalent Fractions
The fractions having the same value are called equivalent fractions. Their numerator and denominator can be different but, they represent the same part of a whole.
Consider the following:
(i)
\(\frac{1}{2}\)
(ii)
\(\frac{2}{4}\)
(iii)
\(\frac{4}{8}\)
(iv)
\(\frac{8}{16}\)
(v)
\(\frac{5}{10}\)
(vi)
\(\frac{10}{20}\)
(viii)
\(\frac{6}{12}\)
(viii)
\(\frac{3}{6}\)
We can see the shade portion with respect to the whole shape in the figures from (i) to (viii)
In; (i) Shaded to whole shape is half to whole i.e., 1/2(ii) Shaded to whole shape is 2 to fourth i.e., 2/4 = 1/2
(iii) Shaded to whole shape is 4 to eighth i.e., 4/8 = 1/2
(iv) Shaded to whole shape is 8 to sixteenth i.e., 8/16 = 1/2
(v) Shaded to whole shape is 5 to tenth i.e., 5/10 = 1/2
(vi) Shaded to whole shape is 10 to 20th i.e., 10/20 = 1/2
(vii) Shaded to whole shape is 6 to 12th i.e., 6/12 = 1/2
(viii) Shaded to whole shape is 3 to 6th i.e., 3/6 = 1/2
Thus, \(\frac{1}{2}\), \(\frac{2}{4}\), \(\frac{4}{8}\), \(\frac{8}{16}\), \(\frac{5}{10}\), \(\frac{10}{20}\), \(\frac{6}{12}\), \(\frac{3}{6}\), etc., each fraction represents half portion of the shape, which are all equal. All have different numerator and denominator but they all have the same value because they represent the same shaded area i.e., half of the rectangle.
So, \(\frac{1}{2}\), \(\frac{2}{4}\), \(\frac{4}{8}\), \(\frac{8}{16}\), \(\frac{5}{10}\), \(\frac{10}{20}\), \(\frac{6}{12}\), \(\frac{3}{6}\) are equivalent fractions.
We can express it as, \(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{4}{8}\) = \(\frac{8}{16}\) = \(\frac{5}{10}\) = \(\frac{10}{20}\) = \(\frac{6}{12}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\).
The
fractions having different numerators and denominators but representing
equal value or magnitude are called equivalent fractions.
Note:
The fraction \(\frac{1}{2}\) and \(\frac{2}{4}\) and \(\frac{4}{8}\) show the same amount of shaded or colored parts. \(\frac{1}{2}\) and \(\frac{2}{4}\) and \(\frac{4}{8}\) are equivalent fractions.
Equivalent fractions are fractions that have different forms but the same value.
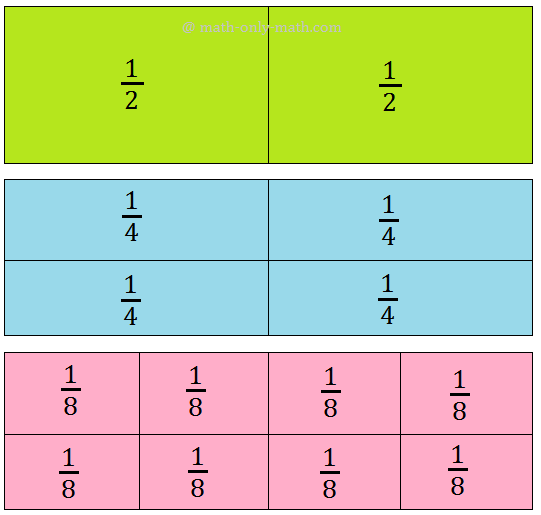
Again, observe the following figures:
We see that the shaded regions in all the figures are the same.
So, the fractions represented by these shaded portions are equal.
Hence, \(\frac{1}{2}\), \(\frac{2}{4}\), \(\frac{3}{6}\), \(\frac{4}{8}\) are equivalent fractions.
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\) = \(\frac{4}{8}\).
Also \(\frac{1}{2}\) = \(\frac{1 × 2}{2 × 2}\) = \(\frac{1 × 3}{2 × 3}\) = \(\frac{1 × 4}{2 × 4}\) and so on.
Again observe the following figures:
We see that the shaded regions in all the circles are the same.
So, the fractions represented by these shaded portions are equal.
Hence, \(\frac{1}{3}\), \(\frac{2}{6}\), \(\frac{3}{9}\), \(\frac{4}{12}\) are equivalent fractions.
Or, \(\frac{1}{3}\) = \(\frac{2}{6}\) = \(\frac{3}{9}\) = \(\frac{4}{12}\) are equivalent fractions.
Also \(\frac{1}{3}\) = \(\frac{1 × 2}{3 × 2}\) = \(\frac{1 × 3}{3 × 3}\) = \(\frac{1 × 4}{3 × 4}\)
Similarly, we can conclude that \(\frac{1}{5}\) = \(\frac{1 × 2}{5 × 2}\) = \(\frac{1 × 3}{5 × 3}\) = \(\frac{1 × 4}{5 × 4}\) = \(\frac{1 × 5}{5 × 5}\) and so on.
Or \(\frac{1}{5}\) = \(\frac{2}{10}\) = \(\frac{3}{15}\) = \(\frac{4}{20}\) = \(\frac{5}{25}\).
Hence, we can say that,
When we multiply the numerator and the denominator of a fraction by the same non- zero number, we get its equivalent fraction.
Again observe the following equivalent fractions \(\frac{2}{7}\), \(\frac{4}{14}\), \(\frac{6}{21}\)
\(\frac{4}{14}\) = \(\frac{4 ÷ 2}{14 ÷ 2}\) = \(\frac{2}{7}\),
\(\frac{6}{21}\) = \(\frac{6 ÷ 3}{21 ÷ 3}\) = \(\frac{2}{7}\)
So,
We see that when the numerator and the denominator of a fraction are divided by the same non-zero number, we get its equivalent fraction.
Building Equivalent Fractions:
1. Change 2/5 to an equivalent fraction with denominator 15.
Note:
Multiply numerator and denominator by the same number to get the required denominator.
2. Change \(\frac{9}{12}\) to an equivalent fraction with denominator 4.
Note:
To find an equivalent fraction with smaller denominator, you can divide the numerator and denominator with the same number.
3. We can build equivalent fraction with multiples of numerator and denominator.
Write the next three equivalent fractions.
Note:
Equivalent fractions have the same value.
Equivalent fraction can be built to very large numbers.
Equivalent fraction can be reduced to the lowest term.
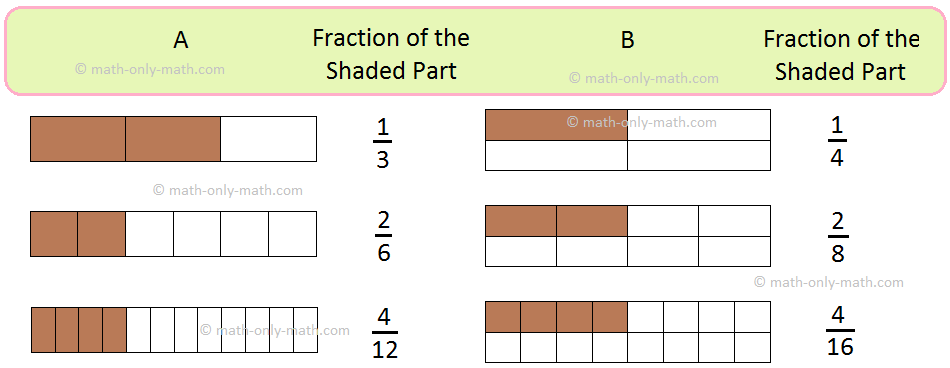
Look at the following:
Look at the figures above.
In A the three different fractions \(\frac{1}{3}\), \(\frac{2}{6}\)
and \(\frac{4}{12}\) represent the same shaded part.
In B the three different fractions \(\frac{1}{4}\), \(\frac{2}{8}\) and \(\frac{4}{16}\) represent the same shaded part.
That is,
\(\frac{1}{3}\) = \(\frac{2}{6}\) = \(\frac{4}{12}\);
\(\frac{1}{4}\) = \(\frac{2}{8}\) = \(\frac{4}{16}\)
Fractions which represent the same part of a whole thing or which indicates the same number of things in a group are called ‘Equivalent Fractions’.
When we multiply the numerator and denominator of a fraction by the same number (other than zero) we get an equivalent fraction with a higher numerator and denominator.
For example;
\(\frac{1 × 2}{6 × 2}\) = \(\frac{2}{12}\)
\(\frac{1 × 3}{6 × 3}\) = \(\frac{3}{18}\)
\(\frac{1 × 4}{6 × 4}\) = \(\frac{4}{24}\)
\(\frac{1}{6}\) = \(\frac{2}{12}\) = \(\frac{3}{18}\) = \(\frac{4}{24}\)
When we divide the numerator and denominator of a fraction by the same number (other than zero) we get an equivalent fraction with a lower numerator and denominator.
For example:
1. \(\frac{36 ÷ 2}{48 ÷ 2}\) = \(\frac{18}{24}\)
\(\frac{18 ÷ 3}{24 ÷ 3}\) = \(\frac{6}{8}\)
\(\frac{6 ÷ 2}{8 ÷ 2}\) = \(\frac{3}{4}\)
\(\frac{3}{4}\) = \(\frac{6}{8}\) = \(\frac{18}{24}\) = \(\frac{36}{48}\)
2. \(\frac{4}{6}\) = \(\frac{.......}{18}\)
Find the relation between the denominators.
6 × ....... = 18 (since 6 < 18)
6 × 3 = 18
Therefore, \(\frac{4 × 3}{6 × 3}\) = \(\frac{12}{18}\)
Therefore, \(\frac{4}{6}\) = \(\frac{12}{18}\)
3. \(\frac{9}{10}\) = \(\frac{27}{.......}\)
Find the relation between the numerators.
6 × ....... = 27 ? (since 9 < 27)
9 × 3 = 27
Therefore, \(\frac{9 × 3}{10 × 3}\) = \(\frac{27}{30}\)
Therefore, \(\frac{9}{10}\) = \(\frac{27}{30}\)
4. \(\frac{24}{32}\) = \(\frac{.......}{8}\)
32 ÷ 8 = 4 (since 32 >8)
\(\frac{24 ÷ 4}{32 ÷ 4}\) = \(\frac{6}{8}\)
Therefore, \(\frac{24}{32}\) = \(\frac{6}{8}\)
Checking for Equivalence of Fractions:
To check whether the given fractions are equivalent or not, we cross-multiply the two fractions. If the products come out to be equal, the fractions are equivalent otherwise they are not.
Cross Product Rule:
If the cross products of two fractions are equal, then they are equivalent fractions.
Note:
Cross multiplication means multiplying the numerator of a fraction with the denominator of the other fraction and multiplying the denominator of the other fraction with the numerator of the first fraction.
For example:
1. Is \(\frac{2}{3}\) equivalent to \(\frac{4}{6}\)?
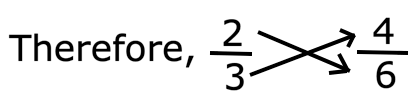
2 × 6 = 12
4 × 3 = 12
Therefore, \(\frac{2}{3}\) is equivalent to \(\frac{4}{6}\)
2. Is \(\frac{2}{4}\) equivalent to \(\frac{3}{5}\)?
2 × 5 = 10
3 × 4 = 12
Therefore, \(\frac{2}{4}\) is not equivalent to \(\frac{3}{5}\)
3. Check whether \(\frac{2}{7}\) and \(\frac{8}{28}\) are equivalent fractions or not.
1st numerator × 2nd denominator = 2 × 28 = 56
1st denominator × 2nd numerator = 7 × 8 = 56
Since the products are equal, \(\frac{2}{7}\) and \(\frac{8}{28}\) are equivalent fractions.
4. Check whether \(\frac{3}{6}\) and \(\frac{5}{15}\) are equivalent fractions or not.
1st numerator × 2nd denominator = 3 × 15 = 45
1st denominator × 2nd numerator = 6 × 5 = 30
Since the products are not equal, \(\frac{3}{6}\) and \(\frac{5}{15}\) are not equivalent fractions.
Solved Examples on Equivalent Fractions:
1. Write the next three equivalent fractions of \(\frac{2}{3}\).
Solution:
Multiply the numerator and the denominator of the given fraction:
by 2, 3, 4 and 5.
\(\frac{2}{3}\) = \(\frac{2 × 2}{3 × 2}\) = \(\frac{4}{6}\);
\(\frac{2}{3}\) = \(\frac{2 × 3}{3 × 3}\) = \(\frac{6}{9}\);
\(\frac{2}{3}\) = \(\frac{2 × 4}{3 × 4}\) = \(\frac{8}{12}\)
So, \(\frac{4}{6}\) , \(\frac{6}{9}\) and \(\frac{8}{12}\) are equivalent fractions of \(\frac{2}{3}\)
2. Find an equivalent fraction of 2/5 with numerator 8.
Solution:
Let \(\frac{2}{5}\) = \(\frac{8}{.....}\)
To get 8 in the numerator, we multiply 2 by 4, and also 5 by 4.
So, \(\frac{2}{5}\) = \(\frac{2 × 4}{5 × 4}\) = \(\frac{8}{20}\)
Hence \(\frac{2}{5}\) and \(\frac{8}{20}\) are equivalent fractions.
3. Find an equivalent fraction of \(\frac{42}{56}\) with numerator 8.
Solution:
Let \(\frac{42}{56}\) = \(\frac{.....}{8}\)
To get 8 in the denominator, we divide 56 by 7 and also 42 by 7.
So \(\frac{42 ÷ 7}{56 ÷ 7}\) = \(\frac{6}{8}\)
Hence \(\frac{42}{56}\) and \(\frac{6}{8}\) are equivalent fractions.
Activity on Equivalent Fractions:
Objective: Understanding equivalent fractions by paper folding.
Materials Required: White sheets of paper, pencil colours.
Procedure/Demonstration: Divide students in groups of 3.
They will be given A-4 sheets or smaller sheets (but all the same size) and asked by the teacher to fold and create the following:
\(\frac{1}{2}\), \(\frac{2}{4}\), \(\frac{4}{8}\)
Each sheet will represent one of the above. They will of course be folded successively by the students. There will be some experimentation in this.
Once they have folded and unfolded, they will need to use colour to shade
\(\frac{1}{2}\), \(\frac{2}{4}\), \(\frac{4}{8}\)
Now, in each group, every bit of fraction will be cut out.
So, each group will have 14 pieces.
Then on direction from the teacher, students will find how many of the smaller pieces cover fully the piece with written on it. They will then paste those together on a separate sheet and present this finding thus.
So, \(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{4}{8}\).
Worksheet on Equivalent Fractions
I. Find 4 equivalent fractions for the given fractions by multiplying.
(i) \(\frac{3}{7}\)
(ii) \(\frac{2}{9}\)
(iii) \(\frac{4}{5}\)
(vi) \(\frac{7}{11}\)
Answers:
I. (i) \(\frac{6}{14}\), \(\frac{9}{21}\), \(\frac{12}{28}\), \(\frac{15}{35}\)
(ii) \(\frac{4}{18}\), \(\frac{6}{27}\), \(\frac{8}{36}\), \(\frac{10}{45}\)
(iii) \(\frac{8}{10}\), \(\frac{12}{15}\), \(\frac{16}{20}\), \(\frac{20}{25}\)
(vi) \(\frac{14}{22}\), \(\frac{21}{33}\), \(\frac{28}{44}\), \(\frac{35}{55}\)
II. Fill the boxes to make equivalent fractions:
(i) \(\frac{3}{4}\) = \(\frac{……}{16}\)
(ii) \(\frac{5}{9}\) = \(\frac{35}{……}\)
(iii) \(\frac{7}{8}\) = \(\frac{……}{64}\)
(vi) \(\frac{7}{……}\) = \(\frac{63}{99}\)
(v) \(\frac{2}{13}\) = \(\frac{……}{51}\)
(vi) \(\frac{11}{17}\) = \(\frac{……}{51}\)
Answers:
II. (i) 12
(ii) 63
(iii) 56
(vi) 11
(v) 8
(vi) 33
III. Write two equivalent fractions for the following.
(i) \(\frac{2}{3}\), ........., .........
(ii) \(\frac{4}{5}\), ........., .........
(iii) \(\frac{6}{7}\), ........., .........
(iv) \(\frac{1}{5}\), ........., .........
(v) \(\frac{3}{8}\), ........., .........
(vi) \(\frac{5}{10}\), ........., .........
Answer:
III. (i) \(\frac{4}{6}\), \(\frac{6}{9}\)
(ii) \(\frac{8}{10}\), \(\frac{20}{25}\)
(iii) \(\frac{24}{28}\), \(\frac{36}{42}\)
(iv) \(\frac{3}{15}\), \(\frac{10}{50}\)
(v) \(\frac{9}{24}\), \(\frac{21}{56}\)
(vi) \(\frac{5}{10}\), \(\frac{3}{8}\)
IV. Find the missing terms of the following fractions.
(i) \(\frac{1}{7}\) = \(\frac{5}{.......}\)
(ii) \(\frac{3}{4}\) = \(\frac{12}{.......}\)
(iii) \(\frac{25}{100}\) = \(\frac{1}{.......}\)
(iv) \(\frac{55}{100}\) = \(\frac{.......}{20}\)
(v) \(\frac{3}{7}\) = \(\frac{.......}{63}\)
(vi) \(\frac{5}{6}\) = \(\frac{.......}{24}\)
(vii) \(\frac{6}{11}\) = \(\frac{18}{.......}\)
(viii) \(\frac{15}{48}\) = \(\frac{.......}{16}\)
(ix) \(\frac{25}{40}\) = \(\frac{.......}{8}\)
Answer:
IV. (i) 35
(ii) 16
(iii) 4
(iv) 11
(v) 27
(vi) 20
(vii) 33
(viii) 5
(ix) 5
V. Find an equivalent fraction of \(\frac{3}{4}\) with
(i) Numerator 27
(ii) Denominator 28
(iii) Numerator 30
(iv) Denominator 12
Answer:
V. (i) \(\frac{27}{36}\)
(ii) \(\frac{21}{28}\)
(iii) \(\frac{30}{40}\)
(iv) \(\frac{9}{12}\)
VI. Find an equivalent fraction of \(\frac{54}{60}\) with
(i) Numerator 27
(ii) Denominator 10
(iii) Numerator 9
(iv) Denominator 20
Answer:
VI. (i) \(\frac{27}{30}\)
(ii) \(\frac{9}{10}\)
(iii) \(\frac{9}{10}\)
(iv) \(\frac{18}{20}\)
VII. Indicate which of the following pairs of fractions are equivalent:
(i) \(\frac{3}{5}\) and \(\frac{9}{15}\)
(ii) \(\frac{2}{8}\) and \(\frac{10}{40}\)
(iii) \(\frac{5}{7}\) and \(\frac{25}{42}\)
(iv) \(\frac{9}{11}\) and \(\frac{27}{34}\)
(v) \(\frac{4}{13}\) and \(\frac{12}{39}\)
Answer:
VII: (i) Equivalent Fraction
(ii) Equivalent Fraction
(iii) Not Equivalent Fraction
(iv) Not Equivalent Fraction
(v) Equivalent Fraction
VIII. Write the next three equivalent fractions of each of the following:
(i) \(\frac{2}{9}\)
(ii) \(\frac{1}{2}\)
(iii) \(\frac{4}{8}\)
(iv) \(\frac{1}{7}\)
(v) \(\frac{2}{5}\)
(vi) \(\frac{2}{9}\)
(vii) \(\frac{1}{2}\)
(viii) \(\frac{4}{8}\)
(ix) \(\frac{1}{7}\)
(x) \(\frac{2}{5}\)
Answer:
VIII. (i) \(\frac{4}{18}\), \(\frac{6}{27}\), \(\frac{8}{36}\)
(ii) \(\frac{2}{4}\), \(\frac{4}{8}\), \(\frac{6}{12}\)
(iii) \(\frac{8}{16}\), \(\frac{12}{24}\), \(\frac{16}{32}\)
(iv) \(\frac{2}{14}\), \(\frac{3}{21}\), \(\frac{4}{28}\)
(v) \(\frac{4}{10}\), \(\frac{6}{15}\), \(\frac{8}{20}\)
(vi) \(\frac{4}{18}\), \(\frac{6}{27}\), \(\frac{8}{36}\)
(vii) \(\frac{2}{4}\), \(\frac{4}{8}\), \(\frac{6}{12}\)
(viii) \(\frac{8}{16}\), \(\frac{12}{24}\), \(\frac{16}{32}\)
(ix) \(\frac{2}{14}\), \(\frac{3}{21}\), \(\frac{4}{28}\)
(x) \(\frac{4}{10}\), \(\frac{6}{15}\), \(\frac{8}{20}\)
IX. Fill in box with the missing numerator to make the statement true:
(i) \(\frac{1}{3}\) = \(\frac{.....}{15}\)
(ii) \(\frac{.....}{9}\) = \(\frac{30}{54}\)
(iii) \(\frac{3}{4}\) = \(\frac{.....}{20}\)
(iv) \(\frac{.....}{8}\) = \(\frac{27}{72}\)
(v) \(\frac{3}{4}\) = \(\frac{.....}{24}\)
(vi) \(\frac{1}{2}\) = \(\frac{.....}{14}\)
(vii) \(\frac{3}{4}\) = \(\frac{.....}{32}\)
(viii) \(\frac{4}{7}\) = \(\frac{.....}{14}\)
Answer:
IX. (i) 5
(ii) 5
(iii) 15
(iv) 3
(v) 18
(vi) 7
(vii) 24
(viii) 8
X. Fill in each box with the missing denominator to make the statement true:
(i) \(\frac{4}{.....}\) = \(\frac{28}{63}\)
(ii) \(\frac{2}{3}\) = \(\frac{14}{.....}\)
(iii) \(\frac{6}{7}\) = \(\frac{24}{.....}\)
(iv) \(\frac{8}{15}\) = \(\frac{96}{.....}\)
(v) \(\frac{5}{7}\) = \(\frac{15}{.....}\)
(vi) \(\frac{2}{7}\) = \(\frac{6}{.....}\)
(vii) \(\frac{3}{5}\) = \(\frac{24}{.....}\)
(viii) \(\frac{8}{11}\) = \(\frac{16}{.....}\)
Answer:
X. (i) 9
(ii) 21
(iii) 28
(iv) 180
(v) 21
(vi) 21
(vii) 40
(viii) 22
Answer:
XI. (i) Equivalent Fractions.
(ii) Non-equivalent Fractions.
(iii) Equivalent Fractions.
(iv) Non-equivalent Fractions.
(v) Non-equivalent Fractions.
(vi) Equivalent Fractions.
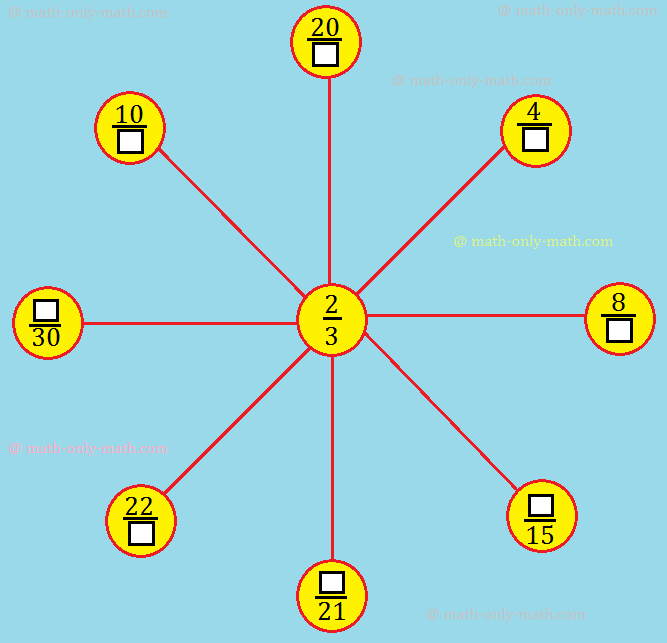
XII. Fill in the boxes to get equivalent fractions.
Answer:
XII: \(\frac{4}{6}\), \(\frac{8}{12}\), \(\frac{10}{15}\), \(\frac{14}{21}\), \(\frac{22}{33}\), \(\frac{20}{30}\), \(\frac{10}{15}\), \(\frac{20}{30}\).
Related Concept
- Fraction of a Whole Numbers
- Representation of a Fraction
- Equivalent Fractions
- Properties of Equivalent Fractions
- Like and Unlike Fractions
- Comparison of Like Fractions
- Comparison of Fractions having the same Numerator
- Types of Fractions
- Changing Fractions
- Conversion of Fractions into Fractions having Same Denominator
- Conversion of a Fraction into its Smallest and Simplest Form
- Addition of Fractions having the Same Denominator
- Subtraction of Fractions having the Same Denominator
- Addition and Subtraction of Fractions on the Fraction Number Line
From Equivalent Fractions to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
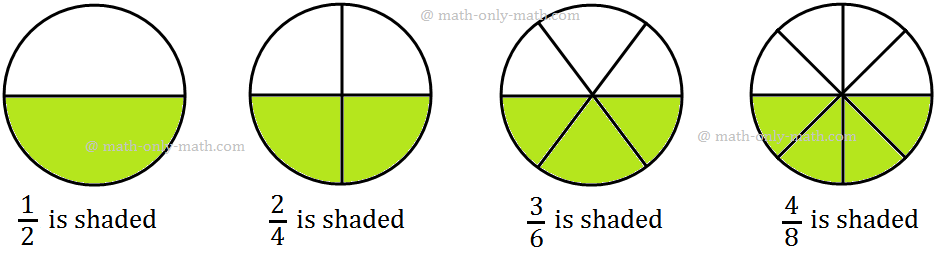
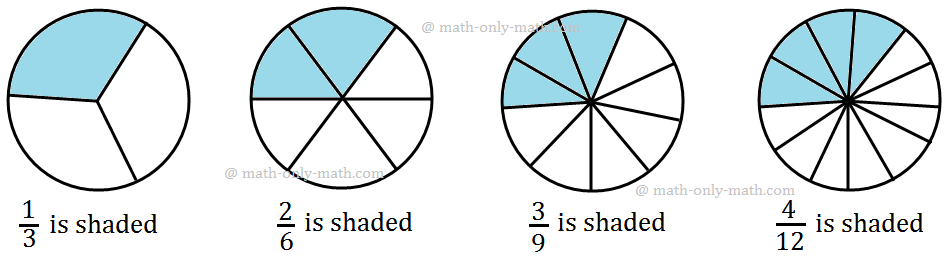
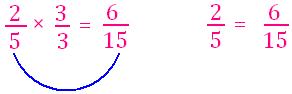
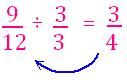


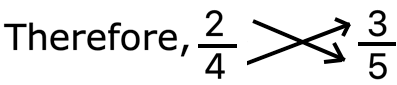

![To convert a percentage into a fraction, place the given number over 100 and reduce it to its lowest term. Consider the following example: (i) 20% [We know % = 1/100]](/image-thumbnails/convert-a-percentage-into-a-fraction.png/default.webp)












New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.