Like and Unlike Fractions

Like and unlike fractions are the two groups of fractions:

(i) 1/5, 3/5, 2/5, 4/5, 6/5

(ii) 3/4, 5/6, 1/3, 4/7, 9/9

In group (i) the denominator of each fraction is 5, i.e., the denominators of the fractions are equal.

The fractions with the same denominators are called like fractions.

In group (ii) the denominator of each fraction is different, i.e., the denominators of all the fractions are different.

The fractions with different denominators are called unlike fractions.

Examples of like fractions are:

(a) (2/9, 3/9, 5/9, 9/9);

(b) (3/10, 7/10, 1/10, 9/10);

(c) (1/7, 2/7, 4/7, 5/7, 7/7)

Examples unlike fractions are:

(a) (1/2, 1/4, 2/3, 5/6)

(b) (3/8, 2/3, 3/5, 2/7)

(c) (1/9, 2/7, 3/4, 2/5).

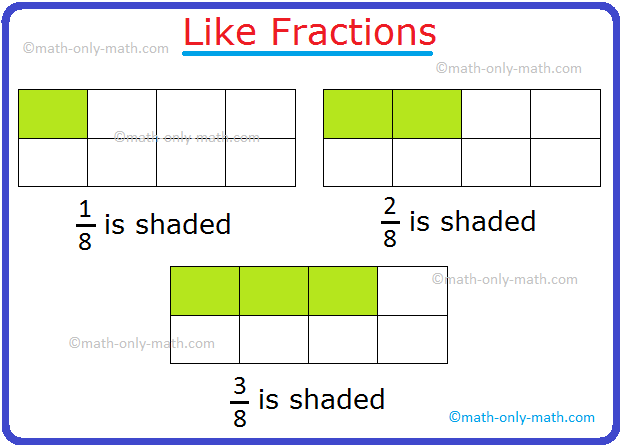
Like Fractions:

Observe the following figures.

$Like Fractions$

The fraction $\frac{1}{8}$ , $\frac{2}{8}$ , $\frac{3}{8}$ have the same denominator. Such fractions are called like fractions.

Unlike Fractions:

$Unlike Fractions$

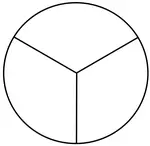
In figure (i) one part is shaded out of 3 parts, the fraction represented is $\frac{1}{3}$ .

In figure (ii) has two parts shaded out of 3 parts, the fraction represented is $\frac{2}{5}$ .

In figure (iii) we have three parts shaded out of 7 parts, the fraction represented is $\frac{3}{7}$ .

The fraction $\frac{1}{3}$ , $\frac{2}{5}$ , $\frac{3}{7}$ have different denominators. Such fractions are called unlike fractions.

Worksheet on Like and Unlike Fractions:

1. Which of the following is a set of like fractions?

(i) $\frac{1}{9}$ , $\frac{5}{9}$ , $\frac{4}{9}$ , $\frac{11}{9}$

(iii) $\frac{4}{11}$ , $\frac{5}{8}$ , $\frac{7}{9}$ , $\frac{1}{7}$

(ii) $\frac{1}{7}$ , $\frac{2}{8}$ , $\frac{4}{19}$ , $\frac{7}{6}$

(iv) $\frac{4}{11}$ , $\frac{5}{8}$ , $\frac{7}{9}$ , $\frac{1}{7}$

Answer:

1. (i) First set is like fractions because denominators are the same.

2. Which of the following is a set of unlike fractions?

(i) $\frac{1}{13}$ , $\frac{13}{15}$ , $\frac{15}{17}$ , $\frac{17}{19}$

(iii) $\frac{4}{16}$ , $\frac{1}{16}$ , $\frac{2}{16}$ , $\frac{9}{16}$

(ii) $\frac{4}{12}$ , $\frac{5}{12}$ , $\frac{8}{12}$ , $\frac{9}{12}$

(iv) $\frac{8}{9}$ , $\frac{1}{7}$ , $\frac{7}{8}$ , $\frac{8}{11}$

Answer:

2. (i) First and fourth sets are unlike fractions because denominators are not the same

You might like these

$In worksheet on word problems on fractions we will solve different types of word problems on multiplication of fractions, word problems on division of fractions etc... 1. How many one-fifths$

Worksheet on Word Problems on Fractions | Fraction Word Problems | Ans
In worksheet on word problems on fractions we will solve different types of word problems on multiplication of fractions, word problems on division of fractions etc... 1. How many one-fifths
$Concept of fractions will help us to express different fractional parts of a whole. One-half When an article or a collection of objects is divided into two equal parts is called as half of the whole.$

2nd Grade Basic Concept of Fractions | Concept of Half, OneThird | Exa
Concept of fractions will help us to express different fractional parts of a whole. One-half When an article or a collection of objects is divided into two equal parts is called as half of the whole.
$How to find fraction as a part of collection? Let there be 14 rectangles forming a box or rectangle. Thus, it can be said that there is a collection of 14 rectangles, 2 rectangles in each row. If it is folded into two halves, each half will have 7 rectangles. So, we can say$

Fraction as a Part of Collection | Pictures of Fraction | Fractional
How to find fraction as a part of collection? Let there be 14 rectangles forming a box or rectangle. Thus, it can be said that there is a collection of 14 rectangles, 2 rectangles in each row. If it is folded into two halves, each half will have 7 rectangles. So, we can say
$Representation of a fraction is discussed here. In a simple fraction, there is a horizontal line. Above this line we write a number which is called the numerator. Below this line we write another number which is called the denominator.$

Representation of a Fraction | Numerator/Denominator | Simple Fraction
Representation of a fraction is discussed here. In a simple fraction, there is a horizontal line. Above this line we write a number which is called the numerator. Below this line we write another number which is called the denominator.
$We will discuss here about the identification of the parts of a fraction. We know fraction means part of something. Fraction tells us, into how many parts a whole has been$

Identification of the Parts of a Fraction | Fractional Numbers | Parts
We will discuss here about the identification of the parts of a fraction. We know fraction means part of something. Fraction tells us, into how many parts a whole has been
$How to find a fraction of a whole number? For finding a fraction of a whole number, we multiply the numerator of the fraction by the given number and then divide the product by the denominator$

Finding a Fraction of a Whole Number | Finding a Fraction of an Amount
How to find a fraction of a whole number? For finding a fraction of a whole number, we multiply the numerator of the fraction by the given number and then divide the product by the denominator
$In 2nd Grade Fractions Worksheet we will solve different types of problems on fractions, one-whole, one-half, one-third, one-fourth, three-fourth or s quarter. In a fraction, it is important that the 'whole' is divided into 'equal' parts.$

2nd Grade Fractions Worksheet | Basic Concept of Fractions | Answers
In 2nd Grade Fractions Worksheet we will solve different types of problems on fractions, one-whole, one-half, one-third, one-fourth, three-fourth or s quarter. In a fraction, it is important that the 'whole' is divided into 'equal' parts.
$In worksheet on fractions, all grade students can practice the questions on fractions on a whole number and also on representation of a fraction. This exercise sheet on fractions can be practiced$

Worksheet on Fractions | Questions on Fractions | Representation | Ans
In worksheet on fractions, all grade students can practice the questions on fractions on a whole number and also on representation of a fraction. This exercise sheet on fractions can be practiced
$To convert a mixed number into an improper fraction, we multiply the whole number by the denominator of the proper fraction and then to the product add the numerator of the fraction to get the numerator of the improper fraction. I$

Conversion of Mixed Fractions into Improper Fractions |Solved Examples
To convert a mixed number into an improper fraction, we multiply the whole number by the denominator of the proper fraction and then to the product add the numerator of the fraction to get the numerator of the improper fraction. I
$We will discuss here about verification of equivalent fractions. To verify that two fractions are equivalent or not, we multiply the numerator of one fraction by the denominator of the other fraction. Similarly, we multiply the denominator of one fraction by the numerator$

Verification of Equivalent Fractions | Exploring Equivalent Fractions
We will discuss here about verification of equivalent fractions. To verify that two fractions are equivalent or not, we multiply the numerator of one fraction by the denominator of the other fraction. Similarly, we multiply the denominator of one fraction by the numerator
$In representations of fractions on a number line we can show fractions on a number line. In order to represent 1/2 on the number line, draw the number line and mark a point A to represent 1.$

Representations of Fractions on a Number Line | Examples | Worksheet
In representations of fractions on a number line we can show fractions on a number line. In order to represent 1/2 on the number line, draw the number line and mark a point A to represent 1.
$Addition and subtraction of fractions are discussed here with examples. To add or subtract two or more fractions, proceed as under: (i) Convert the mixed fractions (if any.) or natural numbers$

Addition and Subtraction of Fractions | Solved Examples | Worksheet
Addition and subtraction of fractions are discussed here with examples. To add or subtract two or more fractions, proceed as under: (i) Convert the mixed fractions (if any.) or natural numbers
$We will discuss here how to arrange the fractions in descending order. Solved examples for arranging in descending order: 1. Arrange the following fractions 5/6, 7/10, 11/20 in descending order. First we find the L.C.M. of the denominators of the fractions to make the$

Fractions in Descending Order |Arranging Fractions an Descending Order
We will discuss here how to arrange the fractions in descending order. Solved examples for arranging in descending order: 1. Arrange the following fractions 5/6, 7/10, 11/20 in descending order. First we find the L.C.M. of the denominators of the fractions to make the
$We will discuss here how to arrange the fractions in ascending order. Solved examples for arranging in ascending order: 1. Arrange the following fractions 5/6, 8/9, 2/3 in ascending order. First we find the L.C.M. of the denominators of the fractions to make the denominators$

Fractions in Ascending Order | Arranging Fractions | Worksheet |Answer
We will discuss here how to arrange the fractions in ascending order. Solved examples for arranging in ascending order: 1. Arrange the following fractions 5/6, 8/9, 2/3 in ascending order. First we find the L.C.M. of the denominators of the fractions to make the denominators
$In 5th Grade Fractions Worksheets we will solve how to compare two fractions, comparing mixed fractions, addition of like fractions, addition of unlike fractions, addition of mixed fractions, word problems on addition of fractions, subtraction of like fractions$

5th Grade Fractions Worksheets | Comparison of Fractions | Addition
In 5th Grade Fractions Worksheets we will solve how to compare two fractions, comparing mixed fractions, addition of like fractions, addition of unlike fractions, addition of mixed fractions, word problems on addition of fractions, subtraction of like fractions

Related Concept

● Fraction of a Whole Numbers

● Representation of a Fraction

● Equivalent Fractions

● Properties of Equivalent Fractions

● Like and Unlike Fractions

● Comparison of Like Fractions

● Comparison of Fractions having the same Numerator

● Types of Fractions

● Changing Fractions

● Conversion of Fractions into Fractions having Same Denominator

● Conversion of a Fraction into its Smallest and Simplest Form

● Addition of Fractions having the Same Denominator

● Subtraction of Fractions having the Same Denominator

● Addition and Subtraction of Fractions on the Fraction Number Line

4th Grade Math Activities

From Like and Unlike Fractions to HOME PAGE

Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.

New! Comments

Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.

Share this page: What’s this?

Facebook X Pinterest WhatsApp Messenger

[?]Subscribe To This Site

$XML RSS$

Recent Articles

Rules of Roman Numeration |Roman Number System|Roman Numeration System
Mar 18, 25 09:41 AM
$Rules of Roman Numerals$
We will learn about Roman Numeration and its rules. We know that there are seven basic Roman Numerals. They are I, V, X, L, C, D and M. These numerals stand for the number 1, 5, 10, 50, 100, 500
Read More
Divisible by 2 | Test of Divisibility by 2 |Rules of Divisibility by 2
Mar 17, 25 04:04 PM
$Divisible by 2$
A number is divisible by 2 if the digit at unit place is either 0 or multiple of 2. So a number is divisible by 2 if digit at its units place is 0, 2, 4, 6 or 8.
Read More
Worksheet on 7 Times Table | Printable Multiplication Table | Video
Mar 17, 25 02:41 PM
$worksheet on multiplication of 7 times table$
Printable worksheet on 7 times table can be used from everywhere. Homeschoolers can also use these multiplication table sheets to practice at home.
Read More
Worksheet on 6 Times Table | Printable Multiplication Table | Video
Mar 16, 25 03:09 PM
$worksheet on multiplication of 6 times table$
Printable worksheet on 6 times table can be used from everywhere. Homeschoolers can also use these multiplication table sheets to practice at home.
Read More
Worksheet on 5 Times Table | Printable Multiplication Table | Video
Mar 16, 25 01:25 PM
$worksheet on multiplication of 5 times table$
Printable worksheet on 5 times table can be used from everywhere. Homeschoolers can also use these multiplication table sheets to practice at home.
Read More

E-mail Address

First Name

Then Don't worry — your e-mail address is totally secure. I promise to use it only to send you Math Only Math.