Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
2nd Grade Basic Concept of Fractions
Concept of fractions will help us to express different fractional parts of a whole.
One Whole:
A whole can be a single object or a collection of objects.
Fractions:
Part of a whole are called fractions.
One-half:
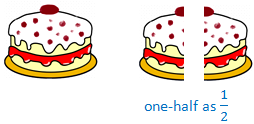
When an article or a collection of objects is divided into two equal parts is called as half of the whole. We express one half by the symbol \(\frac{1}{2}\).
For example, suppose the cake is cut into two equal parts. Each part is called one half of the cake. We write one-half as \(\frac{1}{2}\).
In \(\frac{3}{4}\), the numerator is 3 and the denominator is 4.
Examples on One-half:
1. Richa and Naveen divide a cake into 2 equal parts, and eat one part each.
Each of them gets one-half (\(\frac{1}{2}\)) of the whole cake.
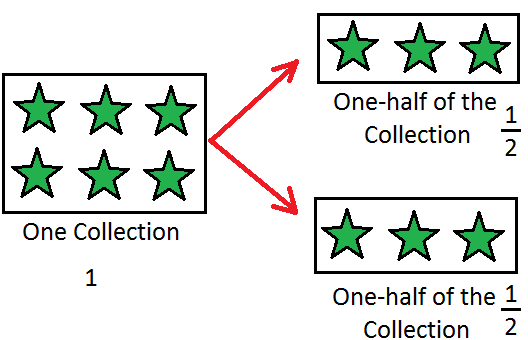
2. Let us take another example. Richard and Thomas want to divide equally 4 balls between them, How many balls would each get?
4 balls can be divided into 2 groups (of 2 balls each).
Each group is one-half of the whole collection. Richard gets 2 balls and Thomas gets 2 balls.
So, one-half of 4 is 2.
Note: In a fraction, it is important that the 'whole' is divided into 'equal' parts.
Half of a Collection:
A fraction is a part of the whole or part of a collection.
A collection of objects can be divided into two equal parts.
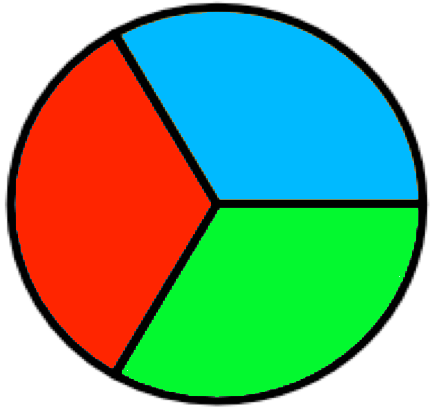
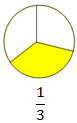
One-Third:
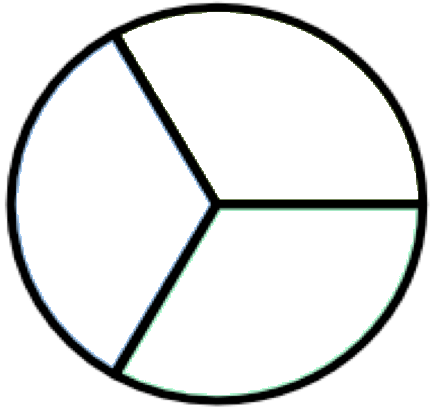
When we divide a whole or a group into three equal parts, each part is called one-third of the whole or a group. We express one third by the symbol \(\frac{1}{3}\).
For example, suppose the biscuit is cut into three equal parts. Each part is called one third of the biscuit. We write one-third as \(\frac{1}{3}\).
Again,
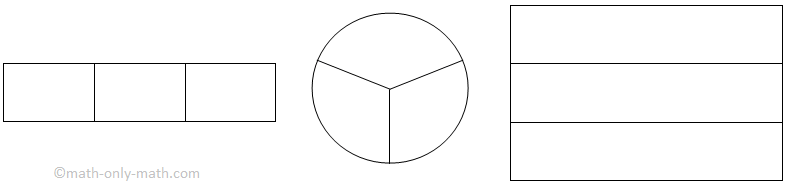
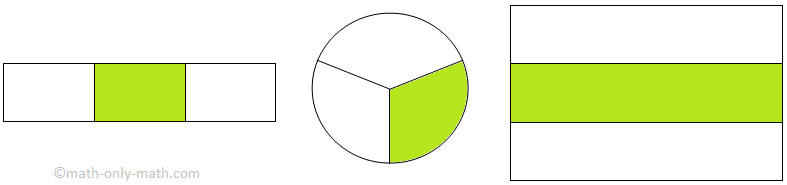
Look at the figures below and find out how many equal parts are there? We find that in each of the following figures the whole is divided into three equal parts.
Each shaded part is one-third of the whole.
When an object is divided into three equal parts, each part is called one-third of the object. It is written as \(\frac{1}{3}\). It is read as one-third.
1. For example, Sarah, Theresa and Ashley together have to make a three-coloured disc for their science exhibition.
They each coloured one-third (\(\frac{1}{3}\)) of the whole disc.
2. Let us take another example.
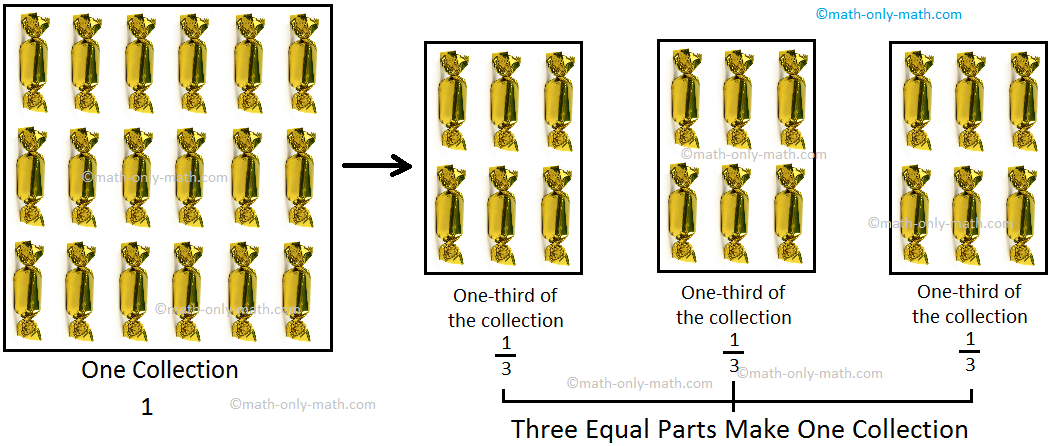
Nancy, Stephanie and Richard want to divide 12 apples equally among themselves
12 apples can be divided into 3 groups (of 4 apples each).
Each group is one-third of the whole collection.
Nancy, Stephanie and Richard get 4 apples each.
So, one-third of 12 is 4.
One-third of a Collection:
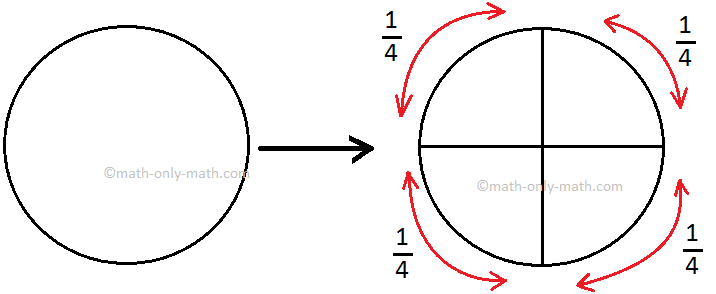
One Fourth:
When we divide a whole or a group into four equal parts, each part is called as one fourth of the whole or the group. We express one fourth by the symbol ¼
For example, suppose the pizza is cut into four equal parts. Each part is one-fourth or one-quarter of the pizza. We write one-fourth as ¼.
There are four members in Michael's family. Michael divides a pizza into 4 equal parts and each one of them gets equal share. When a whole is divided into 4 equal parts, and each part is called one-quarter.
One-quarter is one of four equal parts.
It is written as \(\frac{1}{4}\).
It is read as one-quarter or one-fourth.
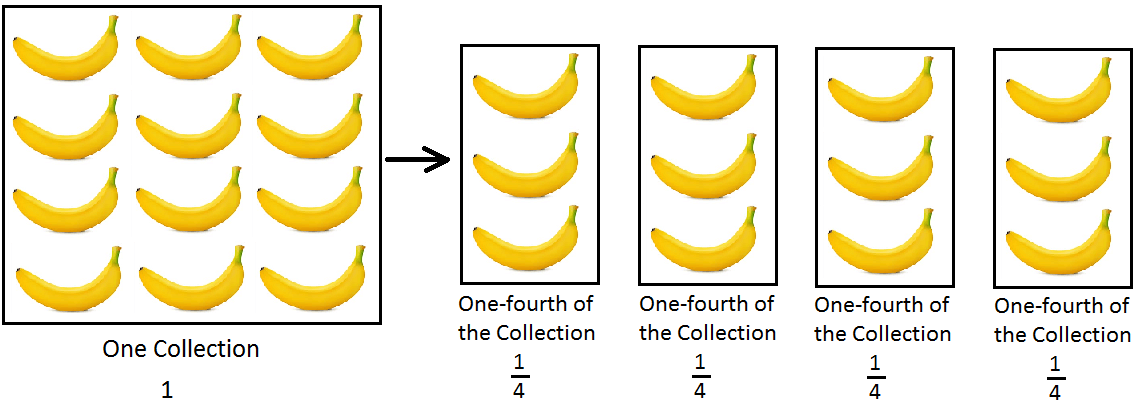
One-Fourth of a Collection:
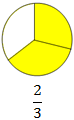
Two-thirds:
When we divide a whole or a group into three equal parts, two parts combined together represent two thirds. We express two thirds by the symbol \(\frac{2}{3}\).
Three-fourths:
When we divide a whole or a group into four equal parts, three parts combined together represent three fourths. We express three fourths by the symbol \(\frac{3}{4}\).
In \(\frac{3}{4}\), the numerator is 3 and the denominator is 4.
Note: The symbol \(\frac{1}{2}\), \(\frac{1}{3}\), \(\frac{1}{4}\), \(\frac{2}{3}\), \(\frac{2}{4}\), etc. are called fractions.
Fractions (third)
|
\(\frac{1}{3}\) tells 1 part out of 3 equal parts.
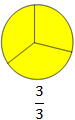
\(\frac{2}{3}\) tells 2 parts out of 3 equal parts. \(\frac{3}{3}\) tells 3 parts out of 3 equal parts. |
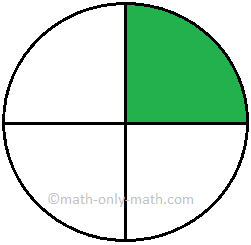
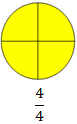
Fractions (fourth)
|
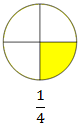
\(\frac{1}{4}\) tells 1 part out of 4 equal parts.
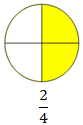
\(\frac{2}{4}\) tells 2 parts out of 4 equal parts.
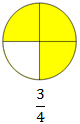
\(\frac{3}{4}\) tells 3 parts out of 4 equal parts. \(\frac{4}{4}\) tells 4 parts out of 4 equal parts. |
The basic concept of fractions are explained above along with the pictures.
SUMMARY:
• Fractions are equal parts of a whole.
• Two-halves make a whole
• Three-thirds make a whole.
• Four-fourths make a whole.
• In a fraction, numerator indicates the parts being chose and the denominator indicates the number of equal parts in all.
Worksheet on 2nd Grade Basic Concept of Fractions:
1. Multiple Choice Questions (MCQ) on 2nd Grade Basic Concept of Fractions:
Tick (✔) the correct option.
(i) \(\frac{1}{3}\) is read as
(a) halves; (b) one-fourth; (c) one-third
(a) two-fourths; (b) one-fourth; (c) three-fourths
(iii) \(\frac{1}{3}\) of 21 =
(a) 6; (b) 4; (c) 7
Answer:
1. (i) → (c) one-third
(ii) → (c) three-fourths
(iii) → (c) 7
2. Write the fraction for the following word problems:
(i) In a Math test of 25 marks, Ashley got 19 marks. What fraction of marks did she get?
(ii) In a book of 36 pages, Anthony read 24. What fraction did he read?
(iii) Christopher bought 5 cans of paint and used 3 cans. What fraction of the paint did he use?
(iv) From her homework of 12 sums, Sarah finished doing 8 sums. What fraction of her homework is not finished?
(v) Seven monkeys were sitting on a tree. One of them had a long tail. What fraction of monkeys had a long tail?
Answer:
2. (i) \(\frac{19}{25}\)
(ii) \(\frac{24}{36}\)
(iii) \(\frac{3}{5}\)
(iv) \(\frac{4}{12}\)
(v) \(\frac{1}{7}\)
FAQ
1. What Is the Meaning of One Half?
1. What Is the Meaning of One Half?
When a whole is divided into two equal parts, each part is called one-half and is written as \(\frac{1}{2}\).
\(\frac{1}{2}\) means, '1 part out of 2 equal parts.'
2. What Is the Meaning of One-Third?
2. What Is the Meaning of One-Third?
When a whole is divided into three equal parts, each part is called one-third and is written as \(\frac{1}{3}\).
\(\frac{1}{3}\) means, '1 part out of 3 equal parts.'
3. What Is the Meaning of One-Fourths?
3. What Is the Meaning of One-Fourths?
When a whole is divided into four equal parts, each part is called one-fourths or a quarter, and is written as \(\frac{1}{4}\).
As the name suggests, \(\frac{1}{4}\) means, '1 part out of 4 equal parts.'
4. What Is the Meaning of three-Fourths?
4. What Is the Meaning of three-Fourths?
As one-fourth means 1 part out of 4 equal parts, similarly three-fourths means 3 parts out of 4 equal parts.
Three-fourths is also called three quarters and is written as \(\frac{3}{4}\)
Fractional Numbers
From 2nd Grade Basic Concept of Fractions to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
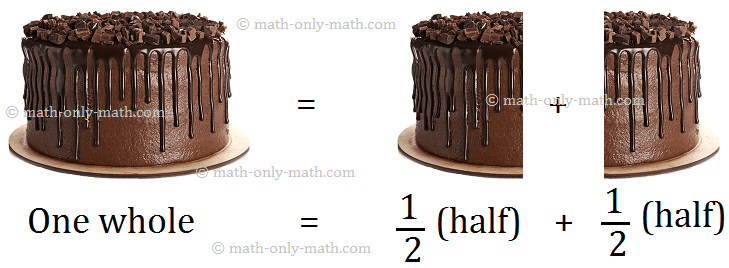


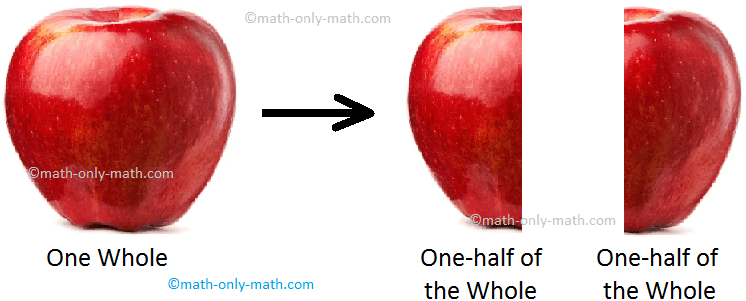




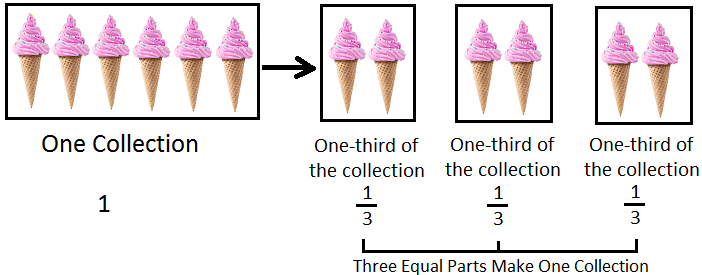






![To convert a percentage into a fraction, place the given number over 100 and reduce it to its lowest term. Consider the following example: (i) 20% [We know % = 1/100]](/image-thumbnails/convert-a-percentage-into-a-fraction.png/default.webp)




New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.