Conversion of Mixed Fractions into Improper Fractions

To convert a mixed number into an improper fraction, we multiply the whole number by the denominator of the proper fraction and then to the product add the numerator of the fraction to get the numerator of the improper fraction. Its denominator is the same as the
denominator of the fractional part i.e.,

In conversion of mixed fractions into improper fractions, we may follow the following steps:

Step I: Obtain the mixed fraction. 

Step II: Identify the whole number and the numerator (top) and denominator (bottom) of the proper fraction.

Step III: Multiply the whole number by the denominator of the proper fraction and add the result to the numerator of the proper fraction.

Step IV: Write the fraction having numerator equal to the number obtained in step III and denominator same as the denominator of the fraction in step II. Thus,

Conversion of Mixed Fractions into Improper Fractions Video

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.

For Example:

1. Convert 3$\frac{5}{6}$ into an improper fraction:

Solution:

3$\frac{5}{6}$ = $\frac{3 × 6 + 5}{6}$ = $\frac{18 + 5}{6}$ = $\frac{23}{6}$

2. Express each of the following mixed fractions as improper fractions:

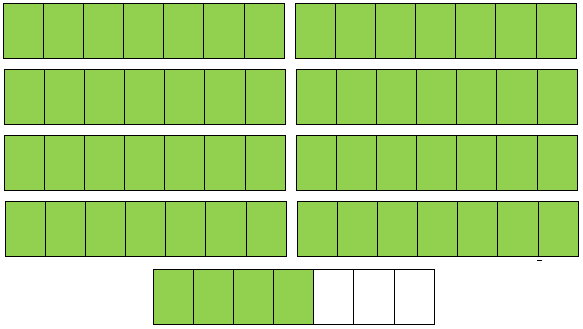
(i) Convert 8$\frac{4}{7}$ into an improper fraction.

8$\frac{4}{7}$ means 8 whole and $\frac{4}{7}$.

                                                           $\frac{4}{7}$

Solution:

8$\frac{4}{7}$ = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + $\frac{4}{7}$

or, 8$\frac{4}{7}$ = $\frac{7}{7}$ + $\frac{7}{7}$ + $\frac{7}{7}$ + $\frac{7}{7}$ + $\frac{7}{7}$ + $\frac{7}{7}$ + $\frac{7}{7}$ + $\frac{7}{7}$ + $\frac{4}{7}$ = $\frac{60}{7}$,           [$\frac{7}{7}$ means 1)

We can also convert a mixed number into an improper fraction as follows.

First multiply the whole number by denominator. Here (8 × 7) + 4 = 60. Now, put the sum as the numerator of the required improper fraction and the denominator remains the same.

8$\frac{4}{7}$ = $\frac{(8 × 7) + 4}{7}$ = $\frac{56 + 4}{7}$ = $\frac{60}{7}$

Thus, 8$\frac{4}{7}$ = $\frac{60}{7}$

(ii) 3$\frac{2}{7}$

= $\frac{(3 × 7) + 2}{7}$

= $\frac{21 + 2}{7}$

= $\frac{23}{7}$

(iii) 4$\frac{5}{9}$

= $\frac{(4 × 9) + 5}{9}$

= $\frac{36 + 5}{9}$

= $\frac{41}{9}$

(iv) 3$\frac{2}{5}$

= $\frac{(3 × 5) + 2}{5}$

= $\frac{15 + 2}{5}$

= $\frac{17}{5}$

(v) 7$\frac{1}{4}$

= $\frac{(7 × 4) + 1}{4}$

= $\frac{28 + 1}{4}$

= $\frac{29}{4}$

Conversion of a Mixed Fraction into an Improper Fraction:

3. Let us convert 5$\frac{4}{5}$ into an improper fraction.

Step I: Multiply the whole number 5 by the denominator 5.  [5 × 5 = 25]

Step II: Add the numerator to it.   [25 + 4 = 29]

Step III: This gives the numerator of the improper fraction.  [$\frac{29}{7}$]

Denominator will remain the same. So. 5$\frac{4}{5}$ = $\frac{29}{7}$

Worksheet on Conversion of Mixed Fractions into Improper Fractions:

1. Convert the following into Improper Fractions:

(i) 4$\frac{1}{3}$

(ii) 2$\frac{1}{2}$

(iii) 4$\frac{2}{3}$

(iv) 7$\frac{4}{9}$

(v) 4$\frac{5}{7}$

Answer:

1. (i) $\frac{13}{3}$

(ii) $\frac{5}{2}$

(iii) $\frac{14}{3}$

(iv) $\frac{67}{9}$

(v) $\frac{33}{7}$

● Fraction

Representations of Fractions on a Number Line

Fraction as Division

Types of Fractions

Conversion of Mixed Fractions into Improper Fractions

Conversion of Improper Fractions into Mixed Fractions

Equivalent Fractions

Interesting Fact about Equivalent Fractions

Fractions in Lowest Terms

Like and Unlike Fractions

Comparing Like Fractions

Comparing Unlike Fractions

Addition and Subtraction of Like Fractions

Addition and Subtraction of Unlike Fractions

Inserting a Fraction between Two Given Fractions

Number Page

6th Grade Page

From Conversion of Mixed Fractions into Improper Fractions to HOME PAGE