5th Grade Fractions Worksheets

In 5th Grade Fractions Worksheets we will solve how to compare two fractions, comparing mixed fractions, addition of like fractions, addition of unlike fractions, addition of mixed fractions, word problems on addition of fractions, subtraction of like fractions, subtraction of unlike fractions, word problems on subtraction of fractions, multiplications of fractions, word problems on multiplication of fractions, fraction of fraction, reciprocal of fractions, division of fractions, word problems on division of fractions.

Let us Summarize the 5th Grade Fraction:

1. A fraction can be represented by three ways:

(i) As a part of a whole

(ii) As a part of a collection

(iii) As division


2. A fraction having numerator 1 is called a unit fraction.

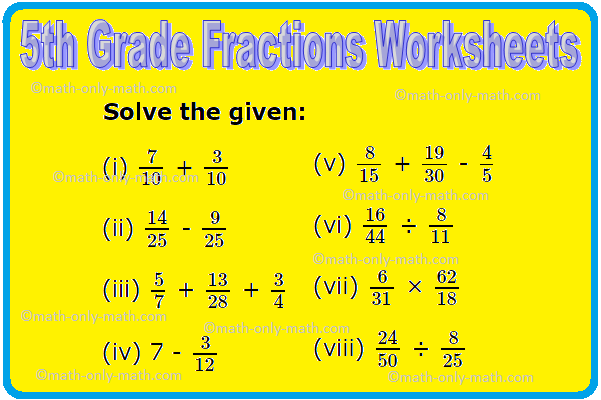
3. Fraction having same denominators are called like fractions.

4. Fraction having different denominators are called unlike fractions.

5. A fraction whose numerator is less than its denominator is called a proper fraction.

6. A fraction whose numerator is greater than its denominator is called an improper fraction.

7. Fractions having equal value are called equivalent fractions.

8. Fractions \(\frac{a}{b}\) and \(\frac{c}{d}\) are equivalent fractions when ad = bc.

9. A combination of a natural number and a proper fraction is called a mixed fraction (number).

10. A fraction is said to be a fraction in its lower terms, if the HCF of a and b is 1. 

11. To reduce a given fraction to its simplest form, we divide both its numerator and denominator by their HCF.

12. Of the two given like fractions, the fraction with greater numerator is greater.

13. Of the two given fractions with same numerator, the fraction with greater denominator is smaller.

5th Grade Fractions Worksheets

I. Answer the following:

(i) The reciprocal of 7\(\frac{1}{8}\) is ………….. .

(ii) 8 boys shared \(\frac{2}{5}\) of a cake equally. What fraction of the cake did each boy get?

(iii) Which is greater 5\(\frac{1}{7}\) or 3\(\frac{1}{7}\)?

(iv) What is the half of 60?

(v) Find the difference between the sum and product of 2\(\frac{1}{4}\) and 1\(\frac{4}{5}\).

(vi) Which is greater \(\frac{23}{25}\) or 1?

(vii) If \(\frac{17}{19}\) of the cup is filled, then what fraction of the cup is empty?

(viii) A family eats 1\(\frac{2}{3}\) cakes in a meal. Will 3 cakes be enough for 2 meals?

Operations on Fractions

II. Solve the given:

(i) \(\frac{7}{10}\) + \(\frac{3}{10}\)

(ii) \(\frac{14}{25}\) - \(\frac{9}{25}\)

(iii) \(\frac{5}{7}\) + \(\frac{13}{28}\) + \(\frac{3}{4}\)

(iv) 7 - \(\frac{3}{12}\)

(v) \(\frac{8}{15}\) + \(\frac{19}{30}\) - \(\frac{4}{5}\)

(vi) \(\frac{16}{44}\) ÷ \(\frac{8}{11}\)

(vii) \(\frac{6}{31}\) × \(\frac{62}{18}\)

(viii) \(\frac{24}{50}\) ÷ \(\frac{8}{25}\)

(ix) \(\frac{13}{18}\) ÷ \(\frac{39}{36}\)

III. Multiplication of three fractions:

(i) \(\frac{2}{7}\) × \(\frac{3}{5}\) × \(\frac{9}{14}\)

(ii) \(\frac{3}{4}\) × 1\(\frac{3}{4}\) × \(\frac{5}{6}\)

(iii) 5\(\frac{1}{2}\) × 4\(\frac{1}{5}\) × 2\(\frac{1}{7}\)

(iv) 4\(\frac{3}{8}\) × 1\(\frac{1}{4}\) × 2\(\frac{1}{2}\)

(v) 3\(\frac{1}{8}\) × 1\(\frac{1}{4}\) × 2\(\frac{3}{8}\)

(vi) 1\(\frac{1}{9}\) × 2\(\frac{5}{13}\) × 1\(\frac{13}{15}\)

(vii) 7\(\frac{1}{7}\) × 2\(\frac{5}{6}\) × 5\(\frac{4}{5}\)

(viii) \(\frac{3}{5}\) × 1\(\frac{1}{3}\) × 1\(\frac{2}{3}\)

IV. Fill in the blanks using properties of multiplication and division of fractions:

(i) \(\frac{1}{5}\) × \(\frac{2}{7}\) = \(\frac{2}{7}\) × \(\frac{.....}{.....}\)

(ii) \(\frac{3}{8}\) × 2\(\frac{4}{5}\) = \(\frac{.....}{.....}\) × \(\frac{3}{8}\)

(iii) 1\(\frac{5}{8}\) × 3\(\frac{2}{7}\) = 3\(\frac{2}{7}\) × \(\frac{.....}{.....}\)

(iv) 9\(\frac{1}{9}\) × 6\(\frac{3}{8}\) = \(\frac{.....}{.....}\) × 9\(\frac{1}{9}\)

(v) 1\(\frac{6}{13}\) × 7 = 7 × \(\frac{.....}{.....}\)

(vi) 2\(\frac{5}{8}\) × 9 = 9 × \(\frac{.....}{.....}\)

(vii) \(\frac{3}{5}\) × \(\frac{.....}{.....}\) = 0

(viii) \(\frac{4}{7}\) × \(\frac{.....}{.....}\) = \(\frac{4}{7}\)

(ix) 1\(\frac{3}{17}\) × 0 = \(\frac{.....}{.....}\)

(x) \(\frac{.....}{.....}\) × 5\(\frac{3}{8}\) = 0

(xi) \(\frac{14}{19}\) ÷ \(\frac{14}{19}\) = \(\frac{.....}{.....}\)

(xii) 6\(\frac{7}{8}\) ÷ 1 = \(\frac{.....}{.....}\)

(xiii) 1\(\frac{3}{4}\) ÷ \(\frac{7}{4}\) = \(\frac{.....}{.....}\)

(xiv) 0 ÷ \(\frac{14}{25}\) = \(\frac{.....}{.....}\)

(xv) 1\(\frac{3}{8}\) ÷ 1\(\frac{3}{8}\) = \(\frac{.....}{.....}\)

(xvi) 0 ÷ \(\frac{29}{37}\) = \(\frac{.....}{.....}\)

(xvii) \(\frac{24}{7}\) ÷ 3\(\frac{3}{7}\) = \(\frac{.....}{.....}\)

(xviii) 0 ÷ 1\(\frac{31}{3}\) = \(\frac{.....}{.....}\)

(xix) 4\(\frac{9}{28}\) ÷ 1 = \(\frac{.....}{.....}\)

(xx) 0 ÷ 2\(\frac{2}{19}\) = \(\frac{.....}{.....}\)

(xxi) 1\(\frac{3}{7}\) ÷ 1 = \(\frac{.....}{.....}\)

(xxii) \(\frac{5}{17}\) ÷ 0 = \(\frac{.....}{.....}\)

(xxiii) \(\frac{1}{8}\) × (\(\frac{1}{10}\) × \(\frac{1}{12}\)) = \(\frac{1}{10}\) × (\(\frac{.....}{.....}\) × \(\frac{1}{12}\)) = \(\frac{.....}{.....}\) × (\(\frac{1}{8}\) × \(\frac{1}{10}\))

(xxiv) 3\(\frac{4}{7}\) × (\(\frac{5}{9}\) × 2\(\frac{3}{4}\)) = \(\frac{.....}{.....}\) × (3\(\frac{4}{7}\) × 2\(\frac{3}{4}\)) = 2\(\frac{3}{4}\) × (\(\frac{.....}{.....}\) × \(\frac{5}{9}\))

Fraction of a Fraction

V. Find the given:

(i) \(\frac{2}{10}\) of 40 mangoes

(ii) \(\frac{3}{15}\) of $75

(iii) \(\frac{3}{4}\) of 20 cups

(iv) \(\frac{3}{7}\) of 1 week

VI. Compare the given fractions and put the right sign <, > or =.

(i) \(\frac{3}{4}\) ……… \(\frac{5}{6}\)

(ii) \(\frac{5}{7}\) ……… \(\frac{15}{21}\)

(i) \(\frac{17}{34}\) ……… \(\frac{8}{32}\)

VII. Convert the given fractions in lowest terms:

(i) \(\frac{15}{60}\)

(ii) \(\frac{22}{77}\)

(iii) \(\frac{18}{54}\)

(iv) \(\frac{36}{60}\)

(v) \(\frac{21}{63}\)

5th Grade Fractions Worksheets

VIII. Multiple Choice Questions on (MCQ) Fractions:

   Tick (✔) the correct option.

(i) A fraction whose denominator is greater than its numerator is called:

(a) an unit fraction

(b) a mixed fraction

(c) a proper fraction

(d) an improper fraction

(ii) A fraction with numerator 1 is called:

(a) unit fraction

(b) proper fraction

(c) like fraction

(d) mixed fraction

(iii) The fraction that represents 8 hours of a day is

(a) \(\frac{8}{12}\)

(b) \(\frac{16}{24}\)

(c) \(\frac{2}{3}\)

(d) \(\frac{1}{3}\)

(iv) A fraction equivalent to \(\frac{32}{20}\) is

(a) \(\frac{8}{5}\)

(b) \(\frac{2}{3}\)

(c) \(\frac{8}{9}\)

(d) \(\frac{8}{6}\)

(v) When we subtract 2\(\frac{2}{3}\) from 5, we get

(a) 3\(\frac{1}{3}\)

(b) 2\(\frac{1}{3}\)

(c) \(\frac{14}{8}\)

(d) none of these

(vi) \(\frac{42}{5}\) when expressed as a mixed fraction is

(a) \(\frac{5}{42}\)

(b) 8\(\frac{2}{5}\)

(c) 2\(\frac{8}{42}\)

(d) none of these

(vii) The value of \(\frac{3}{8}\) + \(\frac{2}{8}\) is

(a) \(\frac{5}{8}\)

(b) \(\frac{3}{8}\)

(c) \(\frac{4}{8}\)

(d) \(\frac{2}{3}\)

(viii) The value of 2\(\frac{2}{3}\) + 2\(\frac{1}{4}\)

(a) 3\(\frac{4}{5}\)

(b) 3\(\frac{5}{12}\)

(c) 4\(\frac{11}{12}\)

(d) none of these

5th Grade Fractions Worksheets

IX. State True or False:

(i) A fraction whose numerator is 1, is called unit fraction.

(ii) \(\frac{1}{4}\), \(\frac{1}{2}\), \(\frac{3}{4}\), \(\frac{7}{8}\) are arranged in descending order.

(iii) Fractions with different denominators are called unlike fractions.

(iv) The fractions with the same denominators are called unlike fractions.

(v) When numerator of a fraction is greater than the denominator, then the fraction is said to be a proper fraction.

X. Fill in the blanks:

(i) \(\frac{5}{9}\) + \(\frac{2}{3}\) - \(\frac{7}{12}\) = _____

(ii) The fraction equivalent to \(\frac{5}{6}\) having numerator 20 is _____.

(iii) If \(\frac{25}{40}\) equivalent to \(\frac{5}{x}\), then x = _____.

(iv) The simplest form of \(\frac{10}{4}\) is _____.

(v) \(\frac{2}{3}\) is _____ than \(\frac{3}{2}\).

XI. Short and Long Answer Type Questions:

(i) Show \(\frac{1}{5}\) on a number line.

(ii) Convert \(\frac{1}{3}\), \(\frac{1}{4}\) and \(\frac{1}{5}\) into like fractions.

(iii) Richard spends \(\frac{1}{3}\) of his income and saves the rest. Joe saves \(\frac{3}{5}\) of his income and spends the rest. Who saves greater part of the income?

(iv) Find the sum: \(\frac{3}{5}\) + \(\frac{6}{7}\) + \(\frac{1}{4}\)

(v) Simplify: 3 - 1\(\frac{1}{4}\) + \(\frac{2}{3}\)

XII. Word Problems on Fractions:

(i) The cost of comic is $57\(\frac{1}{2}\) and that of color book is $25\(\frac{1}{4}\). Which costs more and by how much?

(ii) Tom spent \(\frac{3}{5}\) of his money on bag and spent \(\frac{2}{7}\) of his money on stationary. What fraction of money is left with him?

(iii) Kate has $630. She wants to buy a bag that costs \(\frac{5}{9}\) of the amount she has. What should be the cost of the bag?

(iv) How many pieces of 2\(\frac{3}{4}\) m each can be cut from a string of 16\(\frac{1}{2}\) m length?

Answers on 5th Grade Fractions Worksheets are given below to check the exact answers of the questions. 

Answers:

I. (i) \(\frac{8}{27}\)

(ii) \(\frac{1}{20}\)

(iii) 5\(\frac{1}{7}\)

(iv) 30

(v) 0

(vi) 1

(vii) \(\frac{2}{19}\)

(viii) No, 3\(\frac{1}{3}\) cakes required

II. (i) 1

(ii) \(\frac{1}{5}\)

(iii) 1\(\frac{13}{14}\)

(iv) \(\frac{81}{12}\)

(v) \(\frac{11}{30}\)

(vi) \(\frac{1}{2}\)

(vii) \(\frac{2}{3}\)

(viii) \(\frac{3}{2}\)

(ix) \(\frac{2}{3}\)

III. (i) \(\frac{27}{245}\) 

(ii) 1\(\frac{3}{32}\)

(iii) 49\(\frac{1}{2}\)

(iv) 13\(\frac{43}{64}\)

(v) 9\(\frac{71}{256}\) 

(vi) 4\(\frac{332}{351}\) 

(vii) 117\(\frac{8}{21}\)

(viii) 1\(\frac{1}{3}\) 

IV. (i) \(\frac{1}{5}\)

(ii) 2\(\frac{4}{5}\)

(iii) 1\(\frac{5}{8}\) 

(iv) 6\(\frac{3}{8}\)

(v) 1\(\frac{6}{13}\)

(vi) 2\(\frac{5}{8}\)

(vii) 0

(viii) 1

(ix) 0

(x) 0

(xi) 1

(xii) 6\(\frac{7}{8}\)

(xiii) 1

(xiv) 0

(xv) 1

(xvi) 0

(xvii) 1

(xviii) 0

(xix) 4\(\frac{9}{28}\)

(xx) 0

(xxi) 1\(\frac{3}{7}\)

(xxii) not possible

(xxiii) \(\frac{1}{8}\), (\(\frac{1}{12}\) 

(xxiv) \(\frac{5}{9}\), 3(\(\frac{4}{7}\)

V. (i) 8 mangoes

(ii) $65

(iii) 15 cups

(iv) 3 days

VI. (i) \(\frac{3}{4}\) < \(\frac{5}{6}\)

(ii) \(\frac{5}{7}\) = \(\frac{15}{21}\)

(i) \(\frac{17}{34}\) > \(\frac{8}{32}\)

VII. (i) \(\frac{1}{4}\)

(ii) \(\frac{2}{7}\)

(iii) \(\frac{1}{3}\)

(iv) \(\frac{3}{5}\)

(v) \(\frac{1}{3}\)

VIII. (i) (c) a proper fraction

(ii) (a) unit fraction

(iii) (d) \(\frac{1}{3}\)

(iv) (a) \(\frac{8}{5}\)

(v) (b) 2\(\frac{1}{3}\)

(vi) (b) 8\(\frac{2}{5}\)

(vii) (a) \(\frac{5}{8}\)

(viii) (c) 4\(\frac{11}{12}\)

IX. (i) True

(ii) False

(iii) True

(iv) False

(v) False

X. (i) \(\frac{23}{36}\)

(ii) \(\frac{20}{24}\)

(iii) 8

(iv) \(\frac{5}{2}\)

(v) less

XI. (i) 

(ii) 20/60, 15/60, 12/60

(iii) Joe saves greater part of the income

(iv) 1\(\frac{99}{140}\)

(v) 2\(\frac{5}{12}\)

XII. (i) Comic cost more, $32\(\frac{1}{4}\)

(ii) \(\frac{4}{35}\)

(iii) $350

(iv) 6

5th Grade Fractions Worksheets

5th Grade Math Problems

From 5th Grade Fractions Worksheets to HOME PAGE