Division of Fractions

In division of fractions or dividing fractions requires inverting the divisor, and then proceed the steps as in multiplication.


Reciprocal of a Fraction:

Two fractions are said to be the reciprocal or multiplicative inverse of each other, if their product is 1.

For example:

(i) 3/4 and 4/3 are the reciprocals of each other, because 3/4 × 4/3 = 1.

(ii) The reciprocal of 1/7 is 7/1 i.e.; 7, because 1/7 × 7/1 = 1

(iii) The reciprocal of 1/9 is 9, because 1/9 × 9 = 1

(iv) The reciprocal of 2³/₅ i.e., 13/5 is 5/13, because 2³/₅ × 5/13 = 1.

Reciprocal of 0 does not exist because division by zero is not possible.

Therefore, the reciprocal of a non-zero fraction a/b is the fraction b/a.

Division of fractions:

The division of a fraction a/b by a non-zero fraction c/d is defined as the product of a/b with the multiplicative inverse or reciprocal of c/d.

i.e. a/b ÷ c/d = a/b × d/c

How to divide fractions explain with examples?

There are 3 steps to divide fractions:

Step I: Turn over the second fraction (the one you want to divide by) upside-down (this is now a reciprocal).

Step II: Multiply the first fraction by that reciprocal.

Step III: Simplify the fraction (if possible to its lowest form) .


For example:

(i) 3/5 ÷ 5/9

[Step I: Turn over the second fraction upside-down (it becomes a reciprocal): 5/9 becomes 9/5.]

= 3/5 × 9/5

[Step II: Multiply the first fraction by that reciprocal: (3 × 9)/(5 × 5)]

= 27/25

[Step III: Is not required here since, we cannot simplify]


(ii) 2/3 ÷ 8

[Step I: Turn over the second fraction upside-down (it becomes a reciprocal): 8 = 8/1 becomes 1/8.]

= 2/3 × 1/8

= (2 × 1)/(3 × 8) [Step II: Multiply the first fraction by that reciprocal]

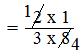
[Step III: Simplify the fraction]

= 1/12

(iii) 4 ÷ 6/7

[Step I: Turn over the second fraction upside-down (it becomes a reciprocal): 6/7 becomes 7/6.]

= 4/1 × 7/6

= (4 × 7)/(1 × 6) [Step II: Multiply the first fraction by that reciprocal]

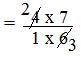
[Step III: Simplify the fraction]

= 14/3

= 4²/₃


(iv) 4²/₃ ÷ 3¹/₂

= 14/3 ÷ 7/2

[Step I: Turn over the second fraction upside-down (it becomes a reciprocal): 7/2 becomes 2/7.]

= 14/3 × 2/7

= (14 × 2)/(3 × 7) [Step II: Multiply the first fraction by that reciprocal]

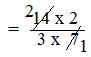
[Step III: Simplify the fraction]

= 4/3

Examples on division of fractions are explained here step by step:

1. Divide the fractions:

(i) 5/9 by 2/3

(ii) 28 by 7/4

(iii) 36 by 6²/₃

(iv) 14/9 by 11


Solution:

(i) 5/9 ÷ 2/3

= 5/9 × 3/2

= (5 × 3)/(9 × 2)

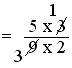
= (5 × 1)/(3 × 2)

= 5/6

(ii) 28 ÷ 7/4

= 28/1 ÷ 7/4

= 28/1 × 4/7

= (28 × 4)/(1 × 7)

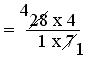
= (4 × 4)/(1 × 1)

= 16/1


(iii) 36 ÷ 6²/₃

= 36 ÷ 20/3

= 36/1 ÷ 20/3

= 36/1 × 3/20

= (36 × 3)/(1 × 20)

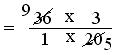
= (9 × 3)/(1 × 5)

= 27/5

= 5²/₅


(iv) 14/9 ÷ 11

= 14/9 ÷ 11/1

= 14/9 × 1/11

= (14 × 1)/(9 × 11)

= 14/99

2. Simplify the fractions:

(i) 4/9 ÷ 2/ 3

(ii) 1⁴/₇ ÷ 5/7

(iii) 3³/₇ ÷ 8/21

(iv) 15³/₅ ÷ 1²³/₄₉


Solution:

(i) 4/9 ÷ 2/3

= 4/9 × 3/2

= (4 × 3)/(9 × 2)

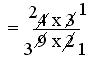
= (2 × 1)/(3 × 1)

= 2/3


(ii) 1⁴/₇ ÷ 5/7

= 11/7 × 7/5

= (11 × 7)/(7 × 5)

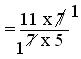
= 11/5


(iii) 3³/₇ ÷ 8/21

= 24/7 ÷ 8/21

= 24/7 × 21/8

= (24 × 21)/(7 × 8)

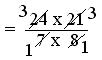
= (3 × 3)/(1 × 1)

= 9


(iv) 15³/₇ ÷ 1²³/₄₉

= 108/ 7 ÷ 72/49

= 108/7 × 49/72

= (108 × 49)/(7 × 72)

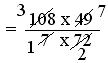
= (3 × 7)/(1 × 2)

= 21/2



3. Simplify the dividing fractions:

(i) (16/5 ÷ 8/20) + (15/5 + 3/35)

(ii) (3/2 ÷ 4/5) + (9/5 × 10/3)


Solution:

(i) (16/5 ÷ 8/20) + (15/5 + 3/35)

= (16/5 × 20/8) + (15/5 × 35/3)

= (16 × 20)/(5 × 8) + (15 × 35)/(5 × 3)

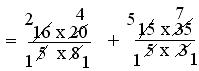
= (3 × 7)/(1 × 2)

= 21/2



3. Simplify the dividing fractions:

(i) (16/5 ÷ 8/20) + (15/5 + 3/35)

(ii) (3/2 ÷ 4/5) + (9/5 × 10/3)


Solution:

(i) (16/5 ÷ 8/20) + (15/5 + 3/35)

= (16/5 × 20/8) + (15/5 × 35/3)

= (16 × 20)/(5 × 8) + (15 × 35)/(5 × 3)

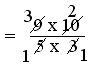
= 15/8 + 6/1

= 15/8 + (6 × 8)/(1 × 8)

= 15/8 + 48/8

= (15 + 48)/8

= 63/8

= 7⁷/₈

Examples on word problems on division of fractions:

1. The cost of 5²/₅ kg of sugar is $ 101¹/₄, find its cost per kg.

Solution:

Cost of 5²/₅ kg of sugar kg of sugar = $ 101¹/₄

Cost of 27/5 kg of sugar = $ 405/4

Cost of 1 kg of sugar

= $ (405/4 ÷ 27/5)

= $ (405/4) × (5/27)

= $ (405 × 5)/(4 × 27)

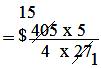
= $ 75/4

= $ 18³/₄

Hence, the cost of 1 kg of sugar is $ 18³/₄.



2. The product of two numbers is 20⁵/₇. If one of the numbers is 6²/₃, find the other.

Solution:

Product of two numbers = 20⁵/₇ = 145/7

One of the numbers is = 6²/₃ = 20/3

The other number = (Product of the numbers ÷ One of the numbers)

= 145 /7 ÷ 3/20

= 145/7 × 3/20

= (145 × 3)/ (7 × 20)

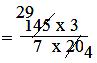
= (29 × 3)/(7 × 4)

= 87/28

= 3³/₂₈

Hence, the other number is 3³/₂₈.

3. By what number should 5⁵/₆ be multiplied to get 3¹/₃?

Solution:

Product of two numbers = 3¹/₃ =10/3

One of the numbers = 5⁵/₆ = 35/6

The other number = Product of the numbers ÷ One of the numbers

The other number = 10/3 ÷ 35/6

= 10/3 × 6/35

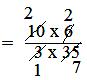
= (2 × 2)/(1 × 7)

= 4/7

Hence, required number is 4/7.

4. If the cost of a notebook is $ 8³/₄, how many notebooks can be purchased for $ 131¹/₄?

Solution:

Cost of one note book = $ 8³/₄ = $ 35/4

Total amount $ 131¹/₄ = $ 525/4

Therefore, number of notebooks = total amount/cost of one note book

= 525/4 ÷ 35/4

= 525/4 × 4/35

= (525 × 4)/(4 × 35)

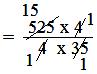
= 15

Hence, 15 notebooks can be purchased for $ 131¹/₄



5. A bucket contains 24³/₄ litres of water. How many 3/4 litre jugs can be filled from the bucket to get it emptied?

Solution:

Volume of water in the bucket = 24³/₄ litres = 99/4litres

Capacity of jug = 3/4 litre

Therefore, number of jugs that can be filled to get the bucket emptied

= 99/4 ÷ 3/4

= 99/4 × 4/3

= (99 × 4)/(4 × 3)

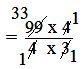
= 33

Hence, 33 jugs of 3/4 litre can be filled to get the bucket emptied.

● Fractions

Fractions

Types of Fractions

Equivalent Fractions

Like and Unlike Fractions

Conversion of Fractions

Fraction in Lowest Terms

Addition and Subtraction of Fractions

Multiplication of Fractions

Division of Fractions

● Fractions - Worksheets

Worksheet on Fractions

Worksheet on Multiplication of Fractions

Worksheet on Division of Fractions

7th Grade Math Problems 

From Division of Fractions to HOMEPAGE