Multiplication of Fractions

In multiplication of fractions to multiply a fraction by one or more natural numbers or fractions, proceed as follows:

(i) Convert the natural numbers (if any) to improper fractions.

(ii) Convert the mixed numbers (if any) to improper fractions.

(iii) Multiply numerator with numerator and denominator with denominator and cancel the common factors of the numerator and denominator and place the product of the numerator over the denominator.

(iv) Convert into mixed fraction if needed.

Product of two fractions =     Product of their numerators
                                                  Product of their denominators

[Place the product of the numerators over the product of the denominators]

i.e., a/b × c/d = (a × c)/(b × d)

There are three steps to multiply fractions are:

1. Multiply the numerators of the fractions (the top numbers).

2. Multiply the denominators of the fractions (the bottom numbers).

3. Simplify the fraction if needed to the lowest terms.



For example:

(i) 3/7 × 4/5

= (3 × 4)/(7 × 5)

= 12/35


(ii) 7/3 × 5/2

= (7 × 5)/(3 × 2)

= 35/6


(iii) 5 × 3/7

= 5/1 × 3/7

= (5 × 3)/(1 × 7)

= 15/7


(iv) 5/12 × 9

= 5/12 × 9/1

= (5 × 9)/(12 × 1)

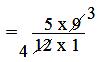
= (5 × 3)/(4 × 1)

= 15/4



Sometimes for indicating multiplication of two fractions, we use the word ‘of ‘as follows:

(i) 1/2 of 8

= 1/2 × 8

= 1/2 × 8/1

= (1 × 8)/(2 × 1)

= 8/2

= 4


(ii) 1/5 of 20

= 1/5 × 20

= 1/5 × 20/1

= 20/5

= 4


(iii) 2/5 of 25

= 2/5 × 25

= 2/5 × 25/1

= (2 × 25)/(5 × 1)

= 50/5

= 10


(iv) 2/3 of 5/7

= 2/3 × 5/7

= (2 ×5)/(3 × 7)

= 10/21.

Examples on multiplication of fractions:

1. Multiply the fractions:

(i) 2/9 by 4/5

(ii) 3/5 by 12

(iii) 2¹/₃ by 2/5

(iv) 5³/₄ by 2³/₇

(i) 2/9 by 4/5

= 2/9 × 4/5

= (2 × 4)/(9 × 5)

= 8/45


(ii) 3/5 by 12

= 3/5 × 12

= 3/5 × 12/1

= (3 × 12)/(5 × 1)

= 36/5

= 7¹/₅


(iii) 2¹/₃ by 2/5

= 2¹/₃ × 2/5

= 7/3 × 2/5

= (7 × 2)/(3 × 5)

= 14/15


(iv) 5³/₄ by 2³/₇

= 5³/₄ × 2³/₇

= 23/4 × 17/7

= (23 × 17)/(4 × 7)

= 391/28

= 13²⁷/₂₈



2. Multiply and reduce to lowest form (if possible) :

(i) 2/5 × 5/4

(ii) 1/3 × 15/8

(iii) 4/5 × 12/7

(iv) 15/16 × 10/12


Solution:

(i) 2/3 × 5/4

= (2 × 5)/(3 × 4)

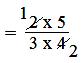
= (1 × 5)/(3 × 2)

= 5/6


(ii) 1/3 × 15/8

= (1 × 15)/(3 × 8)

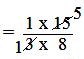
= (1 × 5)/(1 × 8)

= 5/8


(iii) 4/5 × 12/7

= (4 × 12)/(5 × 7)

= 48/35

= 1¹³/₃₅


(iv) 15/16 × 10/12

= (15 × 10)/(16 × 12)

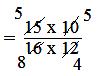
= (5 × 5)/(8 × 4)

= 25/32


3. Simplify the fractions:

(i) 5 × 3/20 × 2/15

(ii) 14/25 × 35/51 × 34/49

(i) 5 × 3/20 × 2/15

Solution:

5 × 3/20 × 2/15

= 5/1 × 3/20 × 2/15

= (5 × 3 × 2)/(1 × 20 × 15)

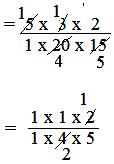
= 1/(2 × 5)

= 1/10


(ii) 14/25 × 35/51 × 34/49

Solution:

14/25 × 35/51 × 34/49

= (14 × 35 × 34)/(25 × 51 × 49)

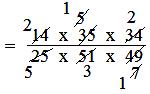
= (2 × 1 × 2)/(5 × 3 × 1)

= 4/15


4. Which is greater? 2/7 of 3/4 or, 3/5 of 5/8.

Solution:

2/7 of 3/4

= 2/7 × 3/4

= (2 × 3)/(7 × 4)

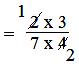
= (1 × 3)/(7 × 2) = 3/14

and,

3/5 of 5/8

= 3/5 × 5/8

= (3 × 5)/(5 × 8)

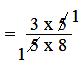
= (3 × 1)/(1 × 8)

= 3/8

In order to compare these fractions, we convert them into equivalent fractions having same denominator equal to the LCM of 14 and 18.

LCM of 14 and 18 = 2 × 7 × 4 = 56

Therefore, 3/14

= (3 × 4)/(14 × 4)

= 12/56

and

3/8

= (3 × 7)/(8 × 7)

= 21/56

In numerator we clearly see i.e., 21 > 12

Therefore, 21/56 > 12/56 ⇒ 3/8 > 3/14

Hence, 3/5 of 5/8 is greater than 2/7 of 3/4.



5. Find:

(i) 3/5 of a dollar

(ii) 3/4 of a year

(iii) 2/3 of a day

(iv) 5/8 of a kilogram

(v) 2/3 of an hour

(vi) 7/25 of a litre


Solution:

(i) 1 dollar = 100 cents

Therefore, 3/5 of a dollar = 3/5 of 100 cents

Now, 3/5 of 100 = 3/5 × 100

= 3/5 × 100/1

= (3 × 100)/(5 × 1)

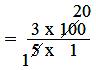
= (3 × 20)/(1 × 1)

= 60

Therefore, 3/5 of a dollar = 60 cents.


(ii) 1 year= 12 months

Therefore, 3/4 of a year = 3/4 of 12 months

Now, 3/4 of 12 = 3/4 ×12

= (3 × 12)/(4 × 1)

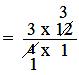
= (3 × 3)/(1 × 1) = 9

Therefore, 3/4 of a year = 9 months


(iii) 2/3 of a day

1 day = 24 hours

Therefore, 2/3 of a day = 2/3 of 24 hours

Now, 2/3 of 24

= 2/3 ×24

= 2/3 × 24/1

= (2 × 24)/(3 × 1)

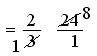
= (2 × 8)/(1 × 1)

= 16

Therefore, 2/3 of a day = 16 hours


(iv) 5/8 of a kilogram

1 kilogram = 1000 grams

Therefore, 5/8 of a kilogram = 5/8 of 1000 grams = (5/8 × 1000) grams

Now, 5/8 × 1000 = 5/8 × 1000/1

= (5 × 1000)/(8 × 1)

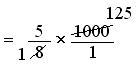
= (5 × 125)/(1 × 1)

= 625

Therefore, 5/8 of a kilogram = 625 grams


(v) 2/3 of an hour

1 hour = 60 minutes

Therefore, 2/3 of an hour = (2/3 × 60) minutes

Now, 2/3 × 60

= 2/3 × 60/1

= (2 × 60)/(3 × 1)

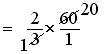
= (2 × 20)/(1 × 1)

= 40

Therefore, 2/3 of an hour = 40 minutes


(vi) 7/25 of a litre

1 litre = 1000 ml

Therefore, 7/25 of a litre = (7/25 × 1000) ml

Now, 7/25 × l000 = 7/25 × 1000/1

= (7 × 1000)/(25 × 1)

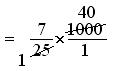
= 7 × 40

= 280

Therefore, 7/25 of a litre = 280 ml.

In multiplying fractions word problems can arise in different situations. We will show you in details some examples step by step.

Examples on word problem on multiplication of fractions:

1. Sugar is sold at $ 17³/₄ per kg. Find the cost of 8¹/₂ kg of a sugar.

Solution:

Cost of 1kg of sugar = $ 17³/₄ = $ 71/4

Therefore, cost of 8¹/₂ kg of sugar = $ (71/4 × 8¹/₂)

= $ (71/4 × 17/2)

= $ (71 × 17)/(4 × 2)

= $ (1207/8)

= $ 150⁷/₈

Hence, the cost of 8¹/₂ kg of sugar is $ 150⁷/₈.



2. A car runs 16 km using 1 litre of petrol car. How much distance will it cover using 2³/₄ litres of petrol?

Solution:

In 1 litre, car runs 16 km

Therefore, in 2³/₄ litres of petrol car will travel = 2³/₄ × 16 km

= 11/4 × 16/1 km

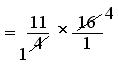
= (11 × 4) km

= 44 km

Hence, car travels 44 km in 2³/₄ litres of petrol.



3. Shelly has read 3/4 of a book consisting of 288 pages. How many pages are still left?

Solution:

Total number of pages in the book = 288

Number of pages read by Shelly = 3/4 of 288

= 3/4 × 288

= 3/4 × 288/1

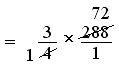
= 3 × 72 = 216

Therefore, number of pages left = (288 - 216) = 72



4. A rectangular park is 20³/₄ m long and 15¹/₂ m wide. What is the area of the park?

Solution:

Length of the park = 20³/₄ m = 83/4 m,

Width of the park = 15¹/₂ m = 31/2 m

Therefore, area of the park = Length × Width

= 83/4 × 31/2 m²

= (83 × 31)/(4 × 2) m²

= 2573/8 m²

= 321⁵/₈ m²

5. Find the area of a square field if its each side is 10³/₄ m long.

Solution:

Length of the square field = 10³/₄ m = 43/4 m.

Breadth of the square field = 10 3/4 m = 43/4 m.

Therefore, area of the square field = Length × Breadth

= 43/4 × 43/4 m²

= (43 × 43)/(4 × 4) m²

= 1849/16 m²

= 115⁹/₁₆ m²

6. Pamela spends 3/5 of her income on household expenses and 1/7 of her income on personal expenses. If her monthly income is $ 35000, find her monthly savings.

Solution:

Pamela’s total monthly income = $ 35000.

Monthly expenditure = 3/5 of $ 35000 + 1/7 of $ 35000

= $ (3/5 × 35O00) + $ (1/7 × 35000)

= $ (3/5 × 35000/1) + $ (1/7 × 35000/1)

= $ (3 × 35000)/(5×1) + $ (1 × 35000)/(7 × 1)

= $ (3 × 7000) + $ (1 × 5000)

= $ 21000 + $ 5000

= $ (21000 + 5000)

= $ 26000

Therefore, monthly savings = $ (35000—26000) = $ 9000



7. A carton contains 40 boxes of nails and each box weighs 3³/₄ kg. How much would a carton of nails weigh?

Solution:

Weight of 1 box = 3³/₄ = 15/4 kg

Therefore, weight of 40 boxes = (15/4 × 40) kg

= (15/4 × 40/1) kg

= (15 × 40)/(4 × 1) kg

= 150 kg

Hence, weight of the carton is 150 kg.

● Fractions

Fractions

Types of Fractions

Equivalent Fractions

Like and Unlike Fractions

Conversion of Fractions

Fraction in Lowest Terms

Addition and Subtraction of Fractions

Multiplication of Fractions

Division of Fractions

● Fractions - Worksheets

Worksheet on Fractions

Worksheet on Multiplication of Fractions

Worksheet on Division of Fractions

7th Grade Math Problems

From Multiplication of Fractions to HOME PAGE