Basic Trigonometric Ratios
and Their Names

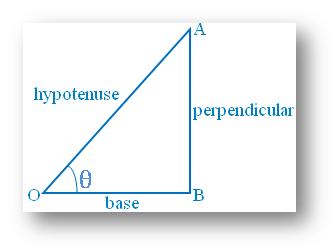
To know about the basic trigonometric ratios and their names with respect to a right-angled triangle.

Let us consider the right-angled triangle ABO as shown in the adjacent figure. Now, with respect to the acute angle ∠AOB = θ, the adjacent side OA becomes the hypotenuse and the other (adjacent) side OB becomes the base. So, in this case AB becomes the perpendicular.

Then AB/OA = perpendicular/hypotenuse = Sine of θ or briefly sin θ

OB/OA = base/hypotenuse = Cosine of θ or briefly cos θ

AB/OB = perpendicular/base = Tangent of θ or briefly tan θ

OA/AB = hypotenuse/perpendicular = Cosecant of θ or briefly cosec θ

OA/OB = hypotenuse/base = Secant of θ or briefly sec θ

OB/AB = base/perpendicular = Cotangent of θ or briefly cot θ

N. B. The side opposite to the angle under reference is to be taken as perpendicular and the side adjacent to it except the hypotenuse as base.

Like all other ratios these ratios are also pure numbers and have no units.

In the beginning of this topic we have become acquainted with the above property. Let us discuss here ore categorically.

Note:

● The side opposite to the angle under reference is to be taken as perpendicular and the side adjacent to it except the hypotenuse as base.

● Like all other ratios these ratios are also pure numbers and have no units.

● In right-angled triangle OBA, ∠BOA lies between 0° to 90° i.e. ∠BOA is acute angle i.e. θ is acute angle and also six trigonometrical ratios are positive.

● Each trigonometrical ratio is a real number.

Now we will discuss about the trigonometrical ratios which are always the same for a given angle:

The trigonometrical ratios of a given angle are defined by the ratios of lengths of two sides of a right-angled triangle. These trigonometrical ratios remain unchanged as long as the angle remains the same i.e., in other words they are independent of the size of the triangle provided the angle remains the same.

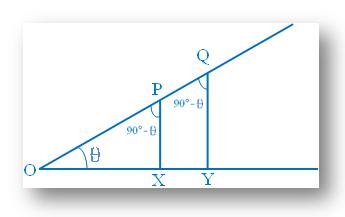
Let, ∠AOA₁ = θ.

Now take any two points M and N on OA₁ and draw MR and NS perpendiculars to OA; again, take any point Q on OA; and draw QP perpendicular to OA₁. According to the definition of trigonometrical ratios we get,

from the right-angled ∆MOR, sin θ = MR/OM ... (i)

from the right-angled ∆NOS, sin θ = NS/ON … (ii)

and from the right-angled ∆QOP, sin θ = QP /OQ……(iii)

Now, the angle θ is common in ∆MOR, ∆NOS, ∆QOP and since each of them are right angle so, ∠MRO = ∠NSO = ∠QPO.

Thus, ∆MOR, ∆NOS are ∆QOP are similar triangle.

Therefore, MR/OM = NS/ON = QP/OQ ……(iv)

Now, from (i), (ii), (iii) and (iv) we understand that the value of sin θ is independent of the size of the triangle from which it is defined provided the angle θ remain the same.

Again similarly we can proof that the values of other trigonometrical ratios (csc θ, cos θ, sec θ, tan θ and cot θ) are also independent of the size of the triangle defining them but depend only on the value of the angle θ.

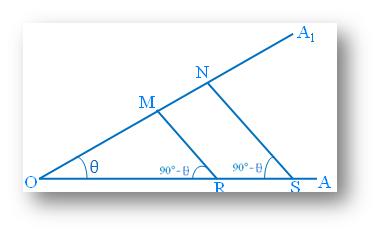
Now, let us discuss here more categorically to proof that the value of the trigonometrical ratio of cos θ is depended only on the value of the angle θ but also independent of the size of the triangle.

Let us suppose that ∠AOA₁ = θ is formed due to change in position of the rotating ray OA to OA₁.

Now, according to the definitions of trigonometncal ratios:

In ∆ POX, Cos θ = OX/OP

In ∆ QOY, Cos θ =OY/OQ

In ∆ ROM, Cos θ =OM/OR

In ∆ SON, Cos θ = ON/OS

But, as the triangles are similar,

Therefore, OX/OP = OY/OQ = OM/OR = ON/OS

So, we can say, that the value of sin θ always remains the same and does not change for change in the sizes of the triangles or the lengths of their sides.

Similarly, this property can be established in case of cos θ, tan θ, .. etc.

We can conclude that the value of each of the trigonometrical ratios with respect to a particular angle is constant.

● Trigonometric Functions

• Basic Trigonometric Ratios and Their Names
• Restrictions of Trigonometrical Ratios
• Reciprocal Relations of Trigonometric Ratios
• Quotient Relations of Trigonometric Ratios
  
• Limit of Trigonometric Ratios
  
• Trigonometrical Identity
• Problems on Trigonometric Identities
• Elimination of Trigonometric Ratios
• Eliminate Theta between the equations
• Problems on Eliminate Theta
• Trig Ratio Problems
• Proving Trigonometric Ratios
• Trig Ratios Proving Problems
• Verify Trigonometric Identities
• Trigonometrical Ratios of 0°
• Trigonometrical Ratios of 30°
• Trigonometrical Ratios of 45°
• Trigonometrical Ratios of 60°
• Trigonometrical Ratios of 90°
• Trigonometrical Ratios Table
• Problems on Trigonometric Ratio of Standard Angle
  
• Trigonometrical Ratios of Complementary Angles
• Rules of Trigonometric Signs
• Signs of Trigonometrical Ratios
  
• All Sin Tan Cos Rule
• Trigonometrical Ratios of (- θ)
• Trigonometrical Ratios of (90° + θ)
• Trigonometrical Ratios of (90° - θ)
• Trigonometrical Ratios of (180° + θ)
• Trigonometrical Ratios of (180° - θ)
• Trigonometrical Ratios of (270° + θ)
• Trigonometrical Ratios of (270° - θ)
• Trigonometrical Ratios of (360° + θ)
• Trigonometrical Ratios of (360° - θ)
• Trigonometrical Ratios of any Angle
• Trigonometrical Ratios of some Particular Angles
• Trigonometric Ratios of an Angle
• Trigonometric Functions of any Angles
• Problems on Trigonometric Ratios of an Angle
• Problems on Signs of Trigonometrical Ratios

11 and 12 Grade Math

From Basic Trigonometric Ratios and their Names to HOME PAGE