Trigonometrical Ratios of 0°

How to find the Trigonometrical Ratios of 0°?

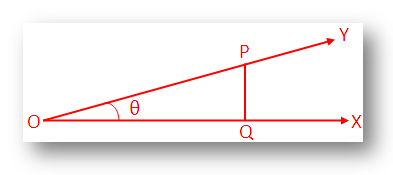
Let a rotating line $\overrightarrow{OX}$ rotates about O in the anti clockwise sense and starting from its initial position $\overrightarrow{OX}$ traces out ∠XOY = θ where θ is very small.

Take a point P on $\overrightarrow{OY}$  and draw $\overline{PQ}$ perpendicular to $\overrightarrow{OX}$  .

Now according to the definition of trigonometric ratio we get,
sin θ = $\frac{\overline{PQ}}{\overline{OP}}$;
cos θ = $\frac{\overline{OQ}}{\overline{OP}}$ and
tan θ = $\frac{\overline{PQ}}{\overline{OQ}}$           

When θ is slowly decreases and finally tends to zero then,
(a) $\overline{PQ}$ slowly decreases and finally tends to zero and

(b) the numerical difference between $\overline{OP}$  and $\overline{OQ}$  becomes very small and finally tends to zero.

Hence, in the Limit when θ → 00 then $\overline{PQ}$ → 0 and $\overline{OP}$   → $\overline{OQ}$  . Therefore, we get
$\lim_{θ \to 0} sin  θ = \lim_{θ \rightarrow 0}\frac{\overline{PQ}}{\overline{OP}} = \frac{0}{\overline{OQ}}$ [since, θ → 0° therefore, $\overline{PQ}$ → 0].
= 0

Therefore sin 0° = 0

$\lim_{θ \rightarrow 0} cos  θ = \lim_{θ \rightarrow 0}\frac{\overline{OQ}}{\overline{OP}} = \frac{\overline{OQ}}{\overline{OQ}}$, [since, θ → 0° therefore, $\overline{OP}$ → $\overline{OQ}$].
= 1

Therefore cos 0° = 1

$\lim_{θ \rightarrow 0} tan  θ = \lim_{θ \rightarrow 0}\frac{\overline{PQ}}{\overline{OQ}} = \frac{0}{\overline{OQ}}$ [since, θ → 0° therefore, $\overline{PQ}$ → 0].
= 0

Therefore tan 0° = 0

Thus,
csc 0° = $\frac{1}{sin  0°} = \frac{1}{0}$, [since, sin 0° = 0] 
= undefined

Therefore csc 0° = undefined

sec 0° = $\frac{1}{cos  0°} = \frac{1}{1}$, [since, cos 0° = 1] 
= 1

Therefore sec 0° = 1

cot 0° = $\frac{1}{tan  0°} = \frac{1}{0}$, [since, tan 0° = 0] 
= undefined

Therefore cot 0° = undefined

Trigonometrical Ratios of 0 degree are commonly called standard angles and the trigonometrical ratios of these angles are frequently used to solve particular angles.

● Trigonometric Functions

• Basic Trigonometric Ratios and Their Names
• Restrictions of Trigonometrical Ratios
• Reciprocal Relations of Trigonometric Ratios
• Quotient Relations of Trigonometric Ratios
  
• Limit of Trigonometric Ratios
  
• Trigonometrical Identity
• Problems on Trigonometric Identities
• Elimination of Trigonometric Ratios
• Eliminate Theta between the equations
• Problems on Eliminate Theta
• Trig Ratio Problems
• Proving Trigonometric Ratios
• Trig Ratios Proving Problems
• Verify Trigonometric Identities
• Trigonometrical Ratios of 0°
• Trigonometrical Ratios of 30°
• Trigonometrical Ratios of 45°
• Trigonometrical Ratios of 60°
• Trigonometrical Ratios of 90°
• Trigonometrical Ratios Table
• Problems on Trigonometric Ratio of Standard Angle
  
• Trigonometrical Ratios of Complementary Angles
• Rules of Trigonometric Signs
• Signs of Trigonometrical Ratios
  
• All Sin Tan Cos Rule
• Trigonometrical Ratios of (- θ)
• Trigonometrical Ratios of (90° + θ)
• Trigonometrical Ratios of (90° - θ)
• Trigonometrical Ratios of (180° + θ)
• Trigonometrical Ratios of (180° - θ)
• Trigonometrical Ratios of (270° + θ)
• Trigonometrical Ratios of (270° - θ)
• Trigonometrical Ratios of (360° + θ)
• Trigonometrical Ratios of (360° - θ)
• Trigonometrical Ratios of any Angle
• Trigonometrical Ratios of some Particular Angles
• Trigonometric Ratios of an Angle
• Trigonometric Functions of any Angles
• Problems on Trigonometric Ratios of an Angle
• Problems on Signs of Trigonometrical Ratios

11 and 12 Grade Math

From Trigonometrical Ratios of 0° to HOME PAGE

New! Comments

Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.

Share this page: What’s this?

FacebookXPinterestWhatsAppReddit

ShareFacebookXPinterestWhatsAppReddit