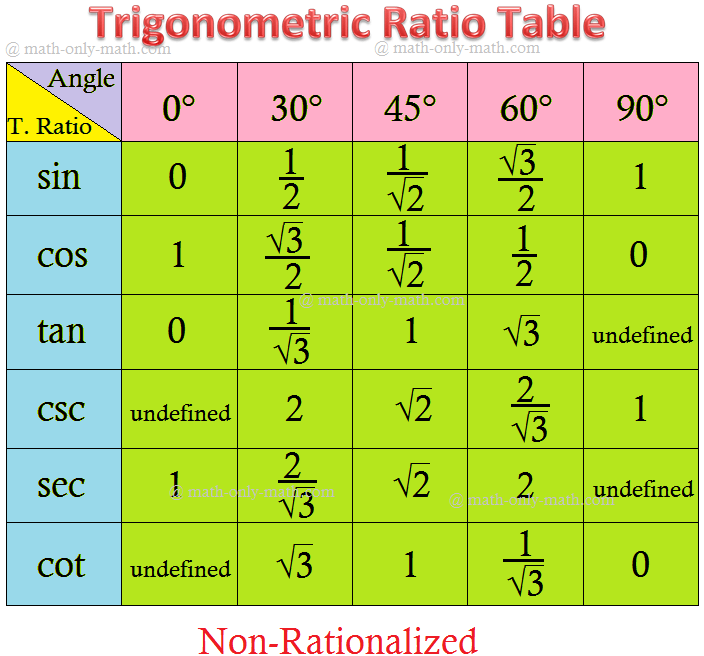
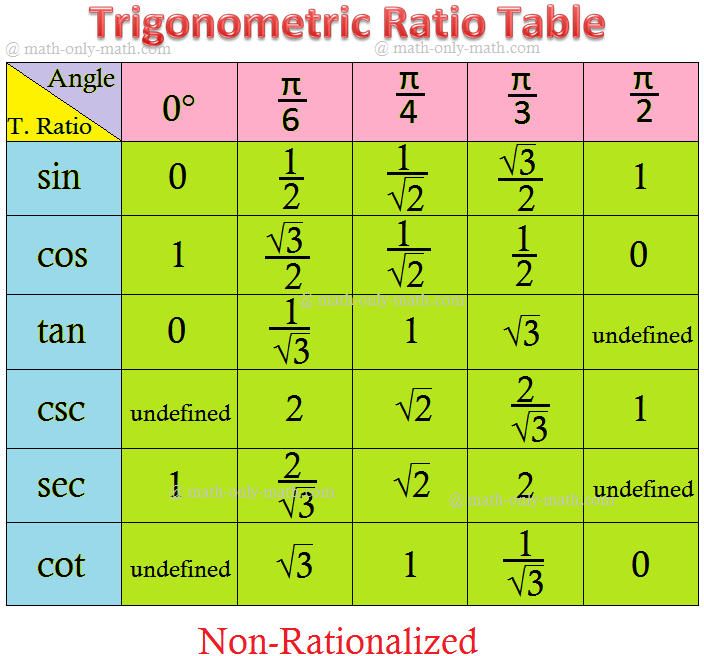
Trigonometrical Ratios Table

The Trigonometrical ratios table will help us to find the values of trigonometric standard angles.

The standard angles of trigonometrical ratios are 0°, 30°, 45°, 60° and 90°.

The values of trigonometrical ratios of standard angles are very important to solve the trigonometrical problems. Therefore, it is necessary to remember the value of the trigonometrical ratios of these standard angles. The sine, cosine and tangent of the standard angles are given below in the table.

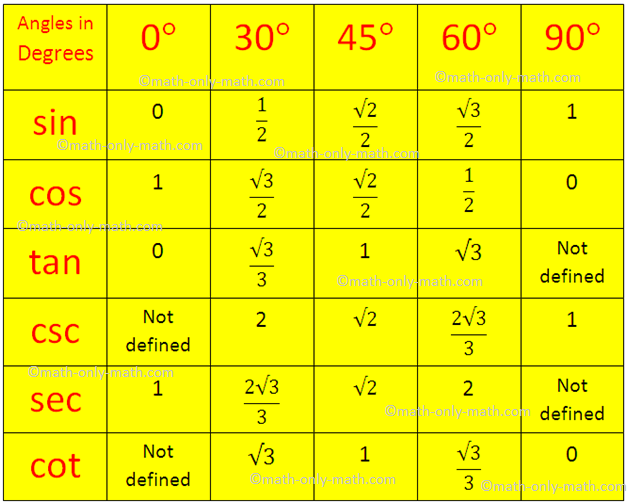
Trigonometric Table in Sexagesimal System:

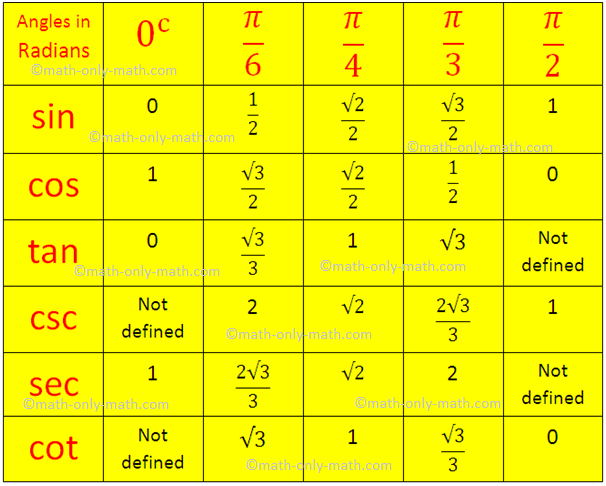
Trigonometric Table in Circular System:

Note: Values of sin θ and cos θ lies between 0 and 1 (both inclusive)

To remember the above values:

(a) divide the numbers 0, 1, 2, 3 and 4 by 4,

(b) take the positive square roots,

(c) these numbers given the values of sin 0°, sin 30°, sin 45°, sin 60° and sin 90° respectively.

(d) write the values of sin 0°, sin 30°, sin 45°, sin 60° and sin 90° in reverse order and get the values of cos 0°, cos 30°, cos 45°, cos 60° and cos 90° respectively.

If θ be an acute angle, the values of sin θ and cos θ lies between 0 and 1 (both inclusive).

The sine of the standard angles 0°, 30°, 45°, 60° and 90° are respectively the positive square roots of 0/4,1/4, 2/4,3/4 and 4/4  

Therefore,

sin 0° = √(0/4) = 0

sin 30° = √(1/4) = ½

sin 45° = √(2/4) = 1/√2 = √2/2

sin 60° = √3/4 = √3/2;

cos 90° = √(4/4) = 1.

Similarly  cosine of the above standard angels are respectively the positive square roots of 4/4, 3/4, 2/4, 1/4, 0/4

Therefore,

cos 0° = √(4/4) = 1

cos 30° = √(3/4) = √3/2

cos 45° = 1

cos 60° = √(1/4) = 1/2

cos 90° = √(0/4) = 0.

Since, we know the sin and cos value of the standard angles from the trigonometrical ratios table; therefore we can easily find the values of the other trigonometrical ratios of the standard angles.

The tangent of the standard angles 0°, 30°, 45°, 60° and 90°:

tan 0° = 0

tan 30° = √3/3

tan 45° = √(2/4) = 1/√2 = √2/2

tan 60° = √3

tan 90° = not defined.

The cosine of the standard angles 0°, 30°, 45°, 60° and 90°:

csc 0° = not defined.

csc 30° = 2

csc 45° = √2

csc 60° = 2√3/3

csc 90° = 1.

The secant of the standard angles 0°, 30°, 45°, 60° and 90°:

sec 0° = 1

sec 30° = 2√3/3

sec 45° = √2

sec 60° = 2

sec 90° = not defined.

The cotangent of the standard angles 0°, 30°, 45°, 60° and 90°:

cot 0° = not defined.

cot 30° = √3

cot 45° = 1

cot 60° = √3/3

cot 90° = 0

Solved Examples on Trigonometrical Ratios Table:

1. If the csc of an angle complementary to A be \(\frac{2√3}{3}\), find tan A.

Solution:

sec (Complementary of ∠A) = \(\frac{2√3}{3}\)

[Using trigonometric ratio table, the value of csc 60° = \(\frac{2√3}{3}\)]

csc (Complementary of ∠A) = csc 60°

Complementary of ∠A = 60°

∠A = (90° - 60°)

∠A = 30°

Therefore, tan A = tan 30°

                        = \(\frac{√3}{3}\), [From Trig Ratios Table]

2. If A = 30° then show that, 2 sin A cos A = sin 2A

Solution:

L.H.S. = 2 sin A cos A

          = 2 sin 30° cos 30°

[From the Trigonometrical Ratios Table, we get  sin 30° = \(\frac{1}{2}\) and cos 30° = \(\frac{√3}{2}\)]

          = 2 × \(\frac{1}{2}\) × \(\frac{√3}{2}\)

          = \(\frac{√3}{2}\)

R.H.S. = sin 2A

          = sin (2 × 30°)

          = sin 60°

[From the Trigonometrical Ratios Table, we get  sin 60° = \(\frac{√3}{2}\)]

          = \(\frac{√3}{2}\)

Therefore, L.H.S. = R.H.S.

3. If A = 30° then show that, tan 2A = \(\frac{2 tan A}{1 - tan^{2} A}\).

Solution:

L.H.S. = tan 2A

          = tan (2 × 30°)

          = tan 60°

[From the Trigonometrical Ratios Table, we get  tan 60° = √3]

          = √3

R.H.S. = \(\frac{2 tan A}{1 - tan^{2} A}\)

          = \(\frac{2 tan 30°}{1 - tan^{2} 30°}\)

[From the Trigonometric Ratios Table, we get  tan 30° = \(\frac{√3}{3}\)]

          = \(\frac{2 × \frac{√3}{3}}{1 - (\frac{√3}{3})^{2}}\)

          = \(\frac{\frac{2√3}{3}}{1 - \frac{3}{9}}\)

          = \(\frac{\frac{2√3}{3}}{\frac{9}{9} - \frac{3}{9}}\)

          = \(\frac{\frac{2√3}{3}}{\frac{9 - 3}{9}}\)

          = \(\frac{\frac{2√3}{3}}{\frac{6}{9}}\)

          = \(\frac{\frac{2√3}{3}}{\frac{2}{3}}\)

          = \(\frac{2√3}{3}\) × \(\frac{3}{2}\)

          = \(\frac{6√3}{6}\)

          = √3

Therefore, L.H.S. = R.H.S.

4. Find the exact value of sin 45° cos 30° + cos 45° sin 30° using trigonometric table.

Solution:

sin 45° cos 30° + cos 45° sin 30°

Plug-in the exact value of sin 45°, cos 30°, cos 45° and sin 30° from the trig ratios table

= \(\frac{√2}{2}\) × \(\frac{√3}{2}\) + \(\frac{√2}{2}\) × \(\frac{1}{2}\)

= \(\frac{√6}{4}\) + \(\frac{√2}{4}\)

= \(\frac{√6 + √2}{4}\)

5. tan \(\frac{π}{3}\), tan \(\frac{π}{4}\), tan \(\frac{π}{6}\) are in geometric progress. 

Solution:

tan \(\frac{π}{3}\), tan \(\frac{π}{4}\), tan \(\frac{π}{6}\) are in geometric progress if,

tan\(^{2}\) \(\frac{π}{4}\) = tan \(\frac{π}{3}\) × tan \(\frac{π}{6}\)

Let's check 

L.H.S. = tan\(^{2}\) \(\frac{π}{4}\)

          = (1)², [From trig ratios table tan \(\frac{π}{4}\) = 1]

          = 1

R.H.S. = tan \(\frac{π}{3}\) × tan \(\frac{π}{6}\)

           = √3 × \(\frac{√3}{3}\)

           = \(\frac{3}{3}\)

           = 1

Therefore, an\(^{2}\) \(\frac{π}{4}\) = tan \(\frac{π}{3}\) × tan \(\frac{π}{6}\)

Thus, tan \(\frac{π}{3}\), tan \(\frac{π}{4}\), tan \(\frac{π}{6}\) are in G.P. (geometric progress).

6. Find the value of \(\frac{4}{3}\) tan² 60° + 3 cos² 30° - 2 sec² 30° - \(\frac{3}{4}\) cot² 60° using trigonometric table.

Solution:

The given trigonometric expression is 

\(\frac{4}{3}\) tan² 60° + 3 cos² 30° - 2 sec² 30° - \(\frac{3}{4}\) cot² 60°

= \(\frac{4}{3}\) . (√3)²  + 3 . (\(\frac{√3}{2}\))² - 2 . (\(\frac{2}{√3}\))² - \(\frac{3}{4}\) . (\(\frac{1}{√3}\))²

[Since, the value of tan 60° = √3, cos 30° = \(\frac{√3}{2}\), sec 30° = \(\frac{2}{√3}\) and cot 60° = \(\frac{1}{√3}\)]

= \(\frac{4}{3}\) . 3 + 3 . \(\frac{3}{4}\) - 2 . \(\frac{4}{3}\) - \(\frac{3}{4}\) . \(\frac{1}{3}\)

= 4 + \(\frac{9}{4}\) - \(\frac{8}{3}\) - \(\frac{1}{4}\)

= \(\frac{10}{3}\)

= 3\(\frac{1}{3}\)

7. If A = 30°, show that cos 2A = cos² A - sin² A 

Solution:

L.H.S. = cos 2A

          = cos 2 . 30°

          = cos 60°

          = \(\frac{1}{2}\)

R.H.S. = cos² A - sin² A 

           = cos² 30° - sin² 30° 

          = (\(\frac{√3}{2}\))²  - (\(\frac{1}{2}\))²

          = \(\frac{3}{4}\) - \(\frac{1}{4}\)

          = \(\frac{1}{2}\)

Therefore, L.H.S. = R.H.S.

8.  If A = 30°, show that 3 sin A - 4 sin³ A = sin 3A

Solution:

L.H.S. = 3 sin A - 4 sin³ A

          = 3 sin 30° - 4 sin³ 30°

          = 3 . \(\frac{1}{2}\) - 4 (\(\frac{1}{2}\))³

          = \(\frac{3}{2}\) - 4 . \(\frac{1}{8}\)

          = \(\frac{3}{2}\) - \(\frac{1}{2}\)

          = 1

          = sin 90° (Using trigonometric table)

          = sin 3 . 30°

          = sin 3A = R.H.S.

Therefore, L.H.S. = R.H.S.

9. If the cosine of an angle complementary to θ be \(\frac{1}{2}\), find the value of cot θ.

Solution:

Angle complementary to θ is 90° - θ.

Therefore, by question, cos (90° - θ) = \(\frac{1}{2}\) =  cos 60°

Therefore, 90° - θ = 60°

            or, 90° - 60° = θ

            or, θ = 30°

Therefore, cot θ = cot 30° = √3. (Using trigonometric table)

10. Find a value of θ which satisfies the equation cos 3θ = sin 2θ.

Solution:

Since, sin 2θ = cos (90° - 2θ),

Therefore, from the given equation we get,

cos 3θ = sin 2θ = cos (90° - 2θ)

Therefore, 3θ = 90° - 2θ

           ⟹ 3θ + 2θ = 90° - 2θ + 2θ; [Adding 2θ on both sides]

           ⟹ 5θ = 90°

           ⟹ θ = \(\frac{90}{5}\)°

           ⟹ θ = 18°

Therefore, the required value of θ is 18°.

11. Each angle A, B, C of the triangle ABC is acute and sin (B + C - A) = 1, tan (C + A - B) =  √3; find A, B and C.

Solution:

Since A, B, C are the angle of ∆ABC

Therefore, A + B + C = 180°   ................... (i)

Again, sin (B + C - A) = 1 = sin 90°  (Using trigonometry table)

Therefore, B + C - A = 90°   ................... (ii)

[Since each of the angles A, B, C is acute, hence, B + C > A]

And tan (C + A - B) = √3 = tan 60°, (Using trigonometry table)

Therefore, C + A - B = 60°   ................... (iii)

[Since each of the angles A, B, C is acute, hence, C + A > B]

Now we add the equations (ii) and (iii)

We get 

(B + C - A) + (C + A - B) = 90° + 60°

⟹ (B + C - A + C + A - B) = 150°

⟹ 2C = 150°

⟹ C = \(\frac{150}{2}\)°

⟹ C = 75°

Again, we add the equations (i) and (ii)

(A + B + C) + (B + C - A) = 180° + 90°

⟹ (A + B + C + B + C - A) = 270°

⟹ 2B + 2C = 270°

⟹ 2B + 2(75°) = 270°; [Since C= 75°]

⟹ 2B + 150° = 270°

⟹ 2B = 270° - 150°

⟹ 2B = 120°

⟹ 2B = \(\frac{120}{2}\)°

⟹ B = 60°

Again, sin (B + C - A) = 1 = sin 90°

Now, putting the values of B and C in (i) we get,

A + 60° + 75° = 180°

⟹ A + 135° = 180°

⟹ A = 180° - 135°

⟹ A = 45°

Therefore, the required angles are:

A = 45°;   B = 60°;   C = 75°

12.  If (x - 2)(sin \(\frac{π}{3}\) cos \(\frac{π}{6}\) + cos \(\frac{π}{3}\) sin \(\frac{π}{6}\)) = sec³ \(\frac{π}{3}\) + tan⁴ \(\frac{π}{4}\) - cosec² \(\frac{π}{6}\), find the value of x.

Solution:

(x - 2)(sin \(\frac{π}{3}\) cos \(\frac{π}{6}\) + cos \(\frac{π}{3}\) sin \(\frac{π}{6}\)) = sec³ \(\frac{π}{3}\) + tan⁴ \(\frac{π}{4}\) - cosec² \(\frac{π}{6}\)

⟹ (x - 2)(sin 60° cos 30° + cos 60° sin 30°) = sec³ 60° + tan⁴ 45° - cosec² 30°, [Since, π = 180°]

⟹ (x - 2)(\(\frac{√3}{2}\) . \(\frac{√3}{2}\) + \(\frac{1}{2}\) . \(\frac{1}{2}\)) = 2³ + 1⁴ - 2²

⟹ (x - 2)(\(\frac{3}{4}\) + \(\frac{1}{4}\)) = 8 + 1 - 4

⟹ (x - 2)(\(\frac{3 + 1}{4}\)) = 5

⟹ (x - 2)(\(\frac{4}{4}\)) = 5

⟹ (x - 2) (1) = 5

⟹ x - 2 = 5

⟹ x = 5 + 2

⟹ x = 7

Therefore, the value of x = 7.

Worksheet on Trigonometrical Ratios Table:

1. If 30° then show that,

(i) 4 cos³ A - 3 cos A = cos 3A

(ii) \(\frac{1 - tan^{2} A}{1 + tan^{2} A}\) = cos 2A

2. If θ = 60° then prove that,

(i) cos θ = 2 cos² \(\frac{θ}{2}\) - 1 = cos² \(\frac{θ}{2}\) - sin² \(\frac{θ}{2}\)

(ii) \(\frac{2 tan \frac{θ}{2}}{1 + tan^{2}\frac{θ}{2}}\) = sin θ

3. Find the values of:

(i) sin 45° cos 30 deg + cos 45° sin 30°

(ii) cos² \(\frac{π}{4}\) - sin² \(\frac{π}{6}\) + tan² \(\frac{π}{3}\)

(iii) sin³ 30° + 4 cot³ 45° - cosec² 30°

(iv) cos \(\frac{π}{6}\) cot \(\frac{π}{3}\) + 2 . cos² \(\frac{π}{3}\)

Answer:

3. (i) \(\frac{√3 + 1}{2√2}\)

(ii) 3\(\frac{1}{4}\)

(iii) \(\frac{1}{8}\)

(iv) 1

4. Prove that,

(i) \(\frac{(sin  0° + sin  60°)(cos  60° + cot  45°)}{(cot  60° + tan  30°)(cosec  30° - cosec  90°)}\) = \(\frac{9}{8}\)

(ii) cos² 60°, cos² 45°, cos² 30° are in A.P.

(iii) tan² \(\frac{π}{3}\) - 2 tan² \(\frac{π}{4}\) = cot² \(\frac{π}{6}\) - 2 sin² \(\frac{π}{6}\) - \(\frac{3}{4}\) cosec² \(\frac{π}{4}\)

(iv) sec 60°, sec² 45°, sec² 30° are in H.P. (Harmonic Progression)

5. Find x if:

(i) (x + 1)cot² \(\frac{π}{6}\) = 2 cos² \(\frac{π}{3}\) + \(\frac{3}{4}\) sec² \(\frac{π}{4}\) + 4 sin² \(\frac{π}{6}\)

(ii) \(\frac{1 + 2 sin 60° cos 60°}{cos 60° + sin 60°}\) + \(\frac{1 - 2 sin 60° cos 60°}{sin 60° - cos 60°}\) = 2x

Answer:

5. (i) x = 0

(ii) x = \(\frac{√3}{2}\)

6. Solve (ϕ and β are positive acute angles): sin (ϕ - β) = \(\frac{1}{2}\); cos (ϕ + β)= \(\frac{1}{2}\) using trigonometry table.

Answer:

6. ϕ = 45° and β = 45°

7. The angle A of the triangle ABC is obtuse; if sec (B + C) cosec (B - C) = 2 find the angles.

Answer:

7. A = 120°, B = 45° and C = 15°

8. Salve ( 0 ≤ θ ≤ 90°)

(i) tan θ + cot θ = 2

(ii) 2 cos² θ + 5 sin θ = 4

(iii) tan ² θ - (√3 + 1) tan θ + √3 = 0

(iv) sec² θ + tan² θ = 7

(v) 2 sin² θ = 3(1 - cos θ)

(vi) 2 sin θ tan θ + 1 = tan θ + 2 sin θ

(vi) tan θ - cot θ = cosec θ.

Answer:

8. (i) θ = 45°

(ii) θ = 30°

(iii) θ = 45°, 60°

(iv) θ = 60°

(v) θ = 0°, 60°

(vi) θ = 30°, 45°

(vi) θ = 60°

9. Find a value of β for each of the following equations:

(i) sin 4β = cos β

(ii) tan 3β = cot β

(iii) sin 3β = cos 7β

Answer:

9. (i) β = 18°

(ii) β = 22.5°

(iii) β = 9°

10. α,  β, γ are positive angles acute and sin (α + β  - γ) = cos (β + γ - α) = tan (γ + α - β) = 1 , find α,  β, γ.

Answer:

10. α = 67.5°; β = 45°; γ = 22.5°

● Trigonometric Functions

• Basic Trigonometric Ratios and Their Names
• Restrictions of Trigonometrical Ratios
• Reciprocal Relations of Trigonometric Ratios
• Quotient Relations of Trigonometric Ratios
  
• Limit of Trigonometric Ratios
  
• Trigonometrical Identity
• Problems on Trigonometric Identities
• Elimination of Trigonometric Ratios
• Eliminate Theta between the equations
• Problems on Eliminate Theta
• Trig Ratio Problems
• Proving Trigonometric Ratios
• Trig Ratios Proving Problems
• Verify Trigonometric Identities
• Trigonometrical Ratios of 0°
• Trigonometrical Ratios of 30°
• Trigonometrical Ratios of 45°
• Trigonometrical Ratios of 60°
• Trigonometrical Ratios of 90°
• Trigonometrical Ratios Table
• Problems on Trigonometric Ratio of Standard Angle
  
• Trigonometrical Ratios of Complementary Angles
• Rules of Trigonometric Signs
• Signs of Trigonometrical Ratios
  
• All Sin Tan Cos Rule
• Trigonometrical Ratios of (- θ)
• Trigonometrical Ratios of (90° + θ)
• Trigonometrical Ratios of (90° - θ)
• Trigonometrical Ratios of (180° + θ)
• Trigonometrical Ratios of (180° - θ)
• Trigonometrical Ratios of (270° + θ)
• Trigonometrical Ratios of (270° - θ)
• Trigonometrical Ratios of (360° + θ)
• Trigonometrical Ratios of (360° - θ)
• Trigonometrical Ratios of any Angle
• Trigonometrical Ratios of some Particular Angles
• Trigonometric Ratios of an Angle
• Trigonometric Functions of any Angles
• Problems on Trigonometric Ratios of an Angle
• Problems on Signs of Trigonometrical Ratios

11 and 12 Grade Math

From Trigonometrical Ratios Table to HOME PAGE