Subscribe to our YouTube channel for the latest videos, updates, and tips.


Limit of Trigonometric Ratios

In limit of trigonometric ratios we will learn how to find the limits to the values of sin θ, csc θ, cos θ, sec θ, tan θ and cot θ.

According to the definitions of the trigonometrical ratios of a positive acute angle are always positive.


Note:

Remember that the trigonometrical ratios may be positive as well as negative.

Limit of Trigonometric Ratios

We get from the definitions of trigonometrical ratios that,



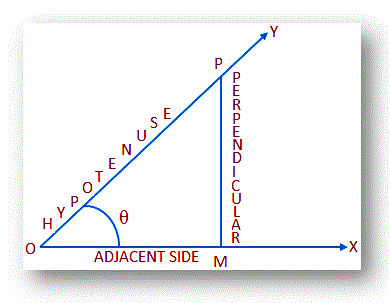
Sin θ = PM/OP and Cos θ = OM/OP …….. (A)

From the above picture, OP is the hypotenuse of the triangle POM; hence, PM ≮ OP and OM ≮ OP.

Therefore, from (A) we get the values of sin θ and cos θ cannot be greater than 1.

Again, csc θ = OP/PM and sec θ = OP/OM

Therefore, it is clearly seen that the values of csc θ and sec θ can never be less than 1.

Finally, tan θ = PM/OM and cot θ = OM/PM

In this case, the values of PM may be greater or less or equal to the values of OM. Thus, the values of tan θ or cot θ may have any non-negative value.

Therefore, the limit of trigonometric ratios of a positive acute angle θ is always non-negative:

(i) The values of sin θ and cos θ cannot be greater than 1;

(ii) The values of csc θ and sec θ cannot be less than 1; and

(iii) The values of tan θ and cot θ can have any value.

● Trigonometric Functions









11 and 12 Grade Math

From Limit of Trigonometric Ratios to HOME PAGE




Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.



New! Comments

Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.




Share this page: What’s this?

Recent Articles

RSS

  1. Expanded form of Decimal Fractions |How to Write a Decimal in Expanded

    May 07, 25 01:48 AM

    Expanded form of Decimal
    Decimal numbers can be expressed in expanded form using the place-value chart. In expanded form of decimal fractions we will learn how to read and write the decimal numbers. Note: When a decimal is mi…

    Read More

  2. Dividing Decimals Word Problems Worksheet | Answers |Decimals Division

    May 07, 25 01:33 AM

    Dividing Decimals Word Problems Worksheet
    In dividing decimals word problems worksheet we will get different types of problems on decimals division word problems, dividing a decimal by a whole number, dividing a decimals and dividing a decima…

    Read More

  3. How to Divide Decimals? | Dividing Decimals by Decimals | Examples

    May 06, 25 01:23 AM

    Dividing a Decimal by a Whole Number
    Dividing Decimals by Decimals I. Dividing a Decimal by a Whole Number: II. Dividing a Decimal by another Decimal: If the dividend and divisor are both decimal numbers, we multiply both the numbers by…

    Read More

  4. Multiplying Decimal by a Whole Number | Step-by-step Explanation|Video

    May 06, 25 12:01 AM

    Multiplying decimal by a whole number is just same like multiply as usual. How to multiply a decimal by a whole number? To multiply a decimal by a whole number follow the below steps

    Read More

  5. Word Problems on Decimals | Decimal Word Problems | Decimal Home Work

    May 05, 25 01:27 AM

    Word problems on decimals are solved here step by step. The product of two numbers is 42.63. If one number is 2.1, find the other. Solution: Product of two numbers = 42.63 One number = 2.1

    Read More