Subscribe to our ▶️YouTube channel🔴 for the latest videos, updates, and tips.
Home | About Us | Contact Us | Privacy | Math Blog
Trigonometric Ratios of an Angle
We will learn how to find the values of trigonometric ratios of an angle. The questions are related to find the values of trigonometric functions of a real number x (i.e., sin x, cos x, tan x, etc.) at any values of x.
1. Find the values of cos (−11Π3)
Solution:
cos (−11Π3) = cos (11Π3), since cos (- θ) = cos θ
= cos (11×180°3)
= cos (1980°3)
= cos 660°
= cos (7 × 90° + 30°)
= sin 30°, [Since the angle 660° lies in the 4th quadrant and cos ratio is positive in this quadrant. Again, in the angle 660° = 7 × 90° + 30°, multiplier of 90° is 7, which is an odd integer ; for this reason cos ratio has changed to sin.]
= 1/2
2. Find the values
of cot (- 855°)
Solution:
cot (- 855°) = - cot
855° [since, cot (-θ) = - cot θ]
= - cot (9 × 90° + 45°)
= - (- tan 45°) [Since the angle 855° = 9 × 90° + 45° lies in the second quadrant and only sin and csc ratios are positive in the second quadrant, thus cot ratio has become negative. Again, in 855° = 9 x 90° + 45°, the number 9 i.e., an odd integer appears as a multiplier of 90°; for this reason cot ratio has changed to tan.]
= tan 45°
= 1.
3. Find the values of csc (-1650°)
Solution:
csc (-1650°) = - csc 1650°, [since, csc (-θ) = - csc θ]
= - csc (18 × 90° + 30°)
= - (- csc 30°), [Since, the angle 1650° lies in the 3th quadrant and csc ratio is negative in this quadrant. Again, in 1650° = 18 × 90° + 30°, multiplier of 90° is 18, which is an even integer; for this reason csc ratio remains unaltered.]
= csc 30°
= 2
4. If sin 49° = 3/4, find the value of sin 581°.
Solution:
sin 581° = sin (7 × 90° - 49°)
= - cos 49°, [Since the angle 581° = 7 × 90° - 49° lies in the 3rd quadrant and only tan and cot ratios are positive in the 3rd quadrant, thus sin ratio has become negative. Again, in 581° = 7 × 90° - 49°, the number 7 i.e., an odd integer appears as a multiplier of 90°; for this reason sin ratio has changed to cos.]
= - √(1- sin2 49°)
= - √1−(34)2
= = - √1−916
= - √16−916, [since, sin 49° = ¾]
= √74
● Trigonometric Functions
- Basic Trigonometric Ratios and Their Names
- Restrictions of Trigonometrical Ratios
- Reciprocal Relations of Trigonometric Ratios
- Quotient Relations of Trigonometric Ratios
- Limit of Trigonometric Ratios
- Trigonometrical Identity
- Problems on Trigonometric Identities
- Elimination of Trigonometric Ratios
- Eliminate Theta between the equations
- Problems on Eliminate Theta
- Trig Ratio Problems
- Proving Trigonometric Ratios
- Trig Ratios Proving Problems
- Verify Trigonometric Identities
- Trigonometrical Ratios of 0°
- Trigonometrical Ratios of 30°
- Trigonometrical Ratios of 45°
- Trigonometrical Ratios of 60°
- Trigonometrical Ratios of 90°
- Trigonometrical Ratios Table
- Problems on Trigonometric Ratio of Standard Angle
- Trigonometrical Ratios of Complementary Angles
- Rules of Trigonometric Signs
- Signs of Trigonometrical Ratios
- All Sin Tan Cos Rule
- Trigonometrical Ratios of (- θ)
- Trigonometrical Ratios of (90° + θ)
- Trigonometrical Ratios of (90° - θ)
- Trigonometrical Ratios of (180° + θ)
- Trigonometrical Ratios of (180° - θ)
- Trigonometrical Ratios of (270° + θ)
- Trigonometrical Ratios of (270° - θ)
- Trigonometrical Ratios of (360° + θ)
- Trigonometrical Ratios of (360° - θ)
- Trigonometrical Ratios of any Angle
- Trigonometrical Ratios of some Particular Angles
- Trigonometric Ratios of an Angle
- Trigonometric Functions of any Angles
- Problems on Trigonometric Ratios of an Angle
- Problems on Signs of Trigonometrical Ratios
11 and 12 Grade Math
From Trigonometric Ratios of an Angle to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
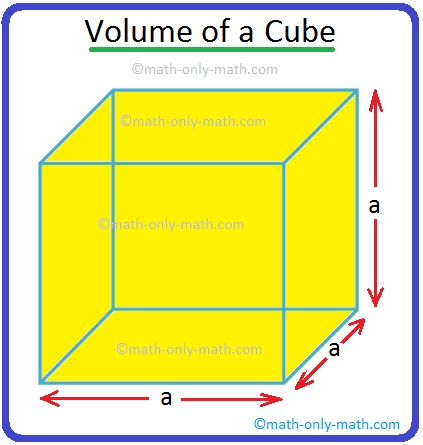
Volume of a Cube | How to Calculate the Volume of a Cube? | Examples
Jul 22, 25 03:02 PM
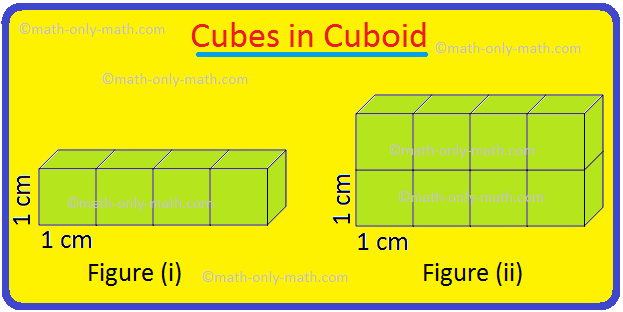
A cube is a solid box whose every surface is a square of same area. Take an empty box with open top in the shape of a cube whose each edge is 2 cm. Now fit cubes of edges 1 cm in it. From the figure i… -
Volume of a Cuboid | Volume of Cuboid Formula | How to Find the Volume
Jul 20, 25 12:58 PM
Cuboid is a solid box whose every surface is a rectangle of same area or different areas. A cuboid will have a length, breadth and height. Hence we can conclude that volume is 3 dimensional. To measur… -
5th Grade Volume | Units of Volume | Measurement of Volume|Cubic Units
Jul 20, 25 10:22 AM
Volume is the amount of space enclosed by an object or shape, how much 3-dimensional space (length, height, and width) it occupies. A flat shape like triangle, square and rectangle occupies surface on… -
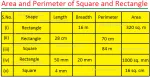
Worksheet on Area of a Square and Rectangle | Area of Squares & Rectan
Jul 19, 25 05:00 AM
We will practice the questions given in the worksheet on area of a square and rectangle. We know the amount of surface that a plane figure covers is called its area. 1. Find the area of the square len… -
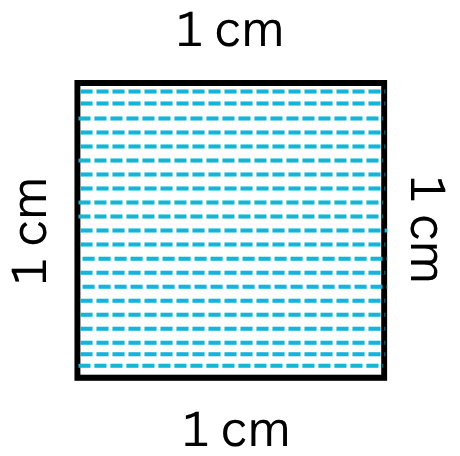
Area of Rectangle Square and Triangle | Formulas| Area of Plane Shapes
Jul 18, 25 10:38 AM
Area of a closed plane figure is the amount of surface enclosed within its boundary. Look at the given figures. The shaded region of each figure denotes its area. The standard unit, generally used for…


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.