Subscribe to our YouTube channel for the latest videos, updates, and tips.
Home | About Us | Contact Us | Privacy | Math Blog
Probability
Probability in everyday life, we come across statements such as:
- Most probably it will rain today.
- Chances are high that the prices of petrol will go up.
- I doubt that he will win the race.
The words ‘most probably’, ‘chances’, ‘doubt’ etc., show the probability of occurrence of an event.
Some Terms Related to Probability
Experiment:
An operation which can produce some well-defined outcomes is called an experiment. Each outcome is called an event.
Random Experiment:
In
an experiment where all possible outcomes are known and in advance if
the exact outcome cannot be predicted, is called a random experiment.
Thus, when we throw a coin we know that all possible outcomes are Head and Tail.
But, if we throw a coin at random, we cannot predict in advance whether its upper face will show a head or a tail.
So, tossing a coin is a random experiment.
Similarly, throwing a dice is a random experiment.
To know more about random experiments in details Click Here.
Trial:
By a trial, we mean performing a random experiment.
For example; throwing a die or tossing a coin etc.
Sample space:
A sample space of an experiment is the set of all possible results of that random experiment.
For example; in throwing a die possible results are {1, 2, 3, 4, 5, 6}.
Event:
Out of the total results obtained from a certain experiment, the set of those results which are in favor of a definite result is called the event and it is denoted as E.
Equally Likely Events:
When there is no reason to expect the happening of one event in preference to the other, then the events are known equally likely events.
For example; when an unbiased coin is tossed the chances of getting a head or a tail are the same.
Exhaustive Events:
All the possible outcomes of the experiments are known as exhaustive events.
For example; in throwing a die there are 6 exhaustive events in a trial.
Favorable Events:
The outcomes which make necessary the happening of an event in a trial are called favorable events.
For example; if two dice are thrown, the number of favorable events of getting a sum 5 is four,
i.e., (1, 4), (2, 3), (3, 2) and (4, 1).
Additive Law of Probability:
If E1 and E2 be any two events (not necessarily mutually exclusive events), then P(E1 ∪ E2) = P(E1) + P(E2) - P(E1 ∩ E2)Probability of Occurrence of an Event:
The probability of occurrence of an event is defined as:
P(occurrence of an event)
= Total number of trials
Solved examples on Probability:
1. A dice is thrown 65 times and 4 appeared 2 1 times. Now, in a random throw of a dice, what is the probability of getting a 4?
Solution:
Total number of tria1s = 65.
Number of times 4 appeared = 21.
= 21/65
2. A survey of 200families shows the results given below:
| No. of girls in the family | 2 | 1 | 0 |
|---|---|---|---|
| |
Out of these families, one is chosen at random. What is the probability that the chosen family has 1 girl?
Solution:
Total number of families = 200.
Number of families having 1 girl = 154.
= Number of families having 1 girl/Total number of families
= 154/200
= 77/100
Worksheet Probability:
1. The tree diagram above represents three events. In the first event either a Red, White, or Blue circle is chosen. In the second event either a Red, White, or Blue circle is chosen. In the third event either a Red, White, or Blue circle is chosen.
Match the following events with the corresponding probabilities:
(a) The second circle is white (a) 10/15
(b) All three circles are red (b) 4/15
(c) Exactly two circles are the same (c) 5/15
(d) At least two circles are the same (d) 3/15
(e) The first circle is not red (e) 1/15
(f) The first two circles are blue (f) 12/15
(g) The third circle is blue (g) 15/15
2. The tree diagram above represents three events. In the first event either an A, B, or C is chosen. In the second event either an A, B, or C is chosen. In the third event either a D, E, or F is chosen.
Match the outcome with its probability:
(a) The second letter is a C (a) 6/12
(b) The first or second letter is an A (b) 0/12
(c) The last letter chosen is a D (c) 5/15
(d) The first two letters chosen are both A (d) 3/15
(e) All three letters are the same (e) 1/15
(f) The first letter is not an A (f) 12/15
(g) ADD (g) 15/15
● Probability
- Probability
- Definition of Probability
- Random Experiments
- Experimental Probability
- Events in Probability
- Empirical Probability
- Coin Toss Probability
- Probability of Tossing Two Coins
- Probability of Tossing Three Coins
- Complimentary Events
- Mutually Exclusive Events
- Mutually Non-Exclusive Events
- Conditional Probability
- Theoretical Probability
- Odds and Probability
- Playing Cards Probability
- Probability and Playing Cards
- Probability Rolling a Die
- Probability for Rolling Two Dice
- Probability for Rolling Three Dice
- Solved Probability Problems
- Probability Questions Answers
- Coin Toss Probability Worksheet
- Worksheet on Playing Cards
- 10th Grade Worksheet on Probability
8th Grade Math Practice
From Probability to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
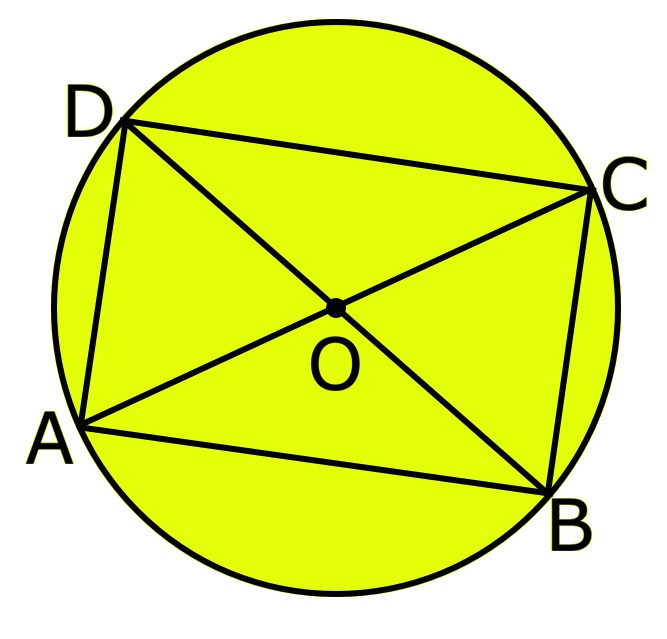
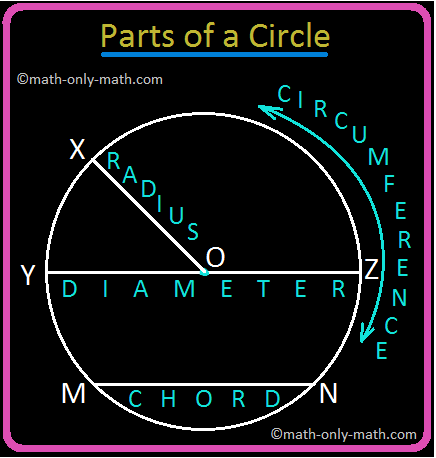
5th Grade Circle Worksheet | Free Worksheet with Answer |Practice Math
Jul 11, 25 02:14 PM
In 5th Grade Circle Worksheet you will get different types of questions on parts of a circle, relation between radius and diameter, interior of a circle, exterior of a circle and construction of circl… -
Construction of a Circle | Working Rules | Step-by-step Explanation |
Jul 09, 25 01:29 AM
Construction of a Circle when the length of its Radius is given. Working Rules | Step I: Open the compass such that its pointer be put on initial point (i.e. O) of ruler / scale and the pencil-end be… -
Combination of Addition and Subtraction | Mixed Addition & Subtraction
Jul 08, 25 02:32 PM
We will discuss here about the combination of addition and subtraction. The rules which can be used to solve the sums involving addition (+) and subtraction (-) together are: I: First add -
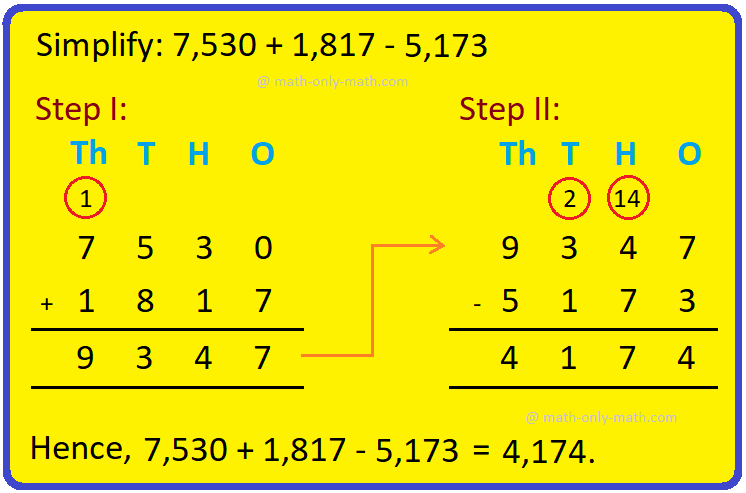
Addition & Subtraction Together |Combination of addition & subtraction
Jul 08, 25 02:23 PM
We will solve the different types of problems involving addition and subtraction together. To show the problem involving both addition and subtraction, we first group all the numbers with ‘+’ and… -
5th Grade Circle | Radius, Interior and Exterior of a Circle|Worksheet
Jul 08, 25 09:55 AM
A circle is the set of all those point in a plane whose distance from a fixed point remains constant. The fixed point is called the centre of the circle and the constant distance is known

New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.