Solved Probability Problems

Solved probability problems and solutions are given here for a concept with clear understanding.

Students can get a fair idea on the probability questions which are provided with the detailed step-by-step answers to every question.

Solved probability problems with solutions:

1.

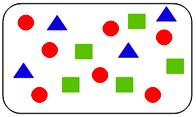
The graphic above shows a container with 4 blue triangles, 5 green squares and 7 red circles. A single object is drawn at random from the container.

Match the following events with the corresponding probabilities:

Solution:

Number of blue triangles in a container = 4

Number of green squares = 5

Number of red circles = 7

Total number of objects = 4 + 5 + 7 = 16

(i) The objects is not a circle:

P(the object is a circle)

= Number of circles/Total number of objects

= 7/16

P(the object is not a circle)

= 1 - P(the object is a circle)

= 1 - 7/16

= (16 - 7)/16

= 9/16

(ii) The objects is a triangle:

P(the object is a triangle)

= Number of triangle/Total number of objects

= 4/16

(iii) The objects is not a triangle:

P(the object is a triangle)

= Number of triangles/Total number of objects

= 4/16

P(the object is not a triangle)

= 1 - P(the object is a triangle)

= 1 - 4/16

= (16 - 4)/16

= 12/16

(iv) The objects is not a square:

P(the object is a square)

= Number of squares/Total number of objects

= 5/16

P(the object is not a square)

= 1 - P(the object is a square)

= 1 - 5/16

= (16 - 5)/16

= 11/16

(v) The objects is a circle:

P(the object is a circle)

= Number of circles/Total number of objects

= 7/16

(vi) The objects is a square:

P(the object is a square)

= Number of squares/Total number of objects

= 5/16

Match the following events with the corresponding probabilities are shown below:

2. A single card is drawn at random from a standard deck of 52 playing cards.

Match each event with its probability.

Note: fractional probabilities have been reduced to lowest terms. Consider the ace as the highest card.

Solution:

Total number of playing cards = 52

(i) The card is a diamond:

Number of diamonds in a deck of 52 cards = 13

P(the card is a diamond)

= Number of diamonds/Total number of playing cards

= 13/52

= 1/4

(ii) The card is a red king:

Number of red king in a deck of 52 cards = 2

P(the card is a red king)

= Number of red kings/Total number of playing cards

= 2/52

= 1/26

(iii) The card is a king or queen:

Number of kings in a deck of 52 cards = 4

Number of queens in a deck of 52 cards = 4

Total number of king or queen in a deck of 52 cards = 4 + 4 = 8

P(the card is a king or queen)

= Number of king or queen/Total number of playing cards

= 8/52

= 2/13

(iv) The card is either a red card or an ace:

Total number of red card or an ace in a deck of 52 cards = 28

P(the card is either a red card or an ace)

= Number of cards which is either a red card or an ace/Total number of playing cards

= 28/52

= 7/13

(v) The card is not a king:

Number of kings in a deck of 52 cards = 4

P(the card is a king)

= Number of kings/Total number of playing cards

= 4/52

= 1/13

P(the card is not a king)

= 1 - P(the card is a king)

= 1 - 1/13

= (13 - 1)/13

= 12/13

(vi) The card is a five or lower:

Number of cards is a five or lower = 16

P(the card is a five or lower)

= Number of card is a five or lower/Total number of playing cards

= 16/52

= 4/13

(vii) The card is a king:

Number of kings in a deck of 52 cards = 4

P(the card is a king)

= Number of kings/Total number of playing cards

= 4/52

= 1/13

(viii) The card is black:

Number of black cards in a deck of 52 cards = 26

P(the card is black)

= Number of black cards/Total number of playing cards

= 26/52

= 1/2

Match the following events with the corresponding probabilities are shown below:

3. A bag contains 3 red balls and 4 black balls. A ball is drawn at random from the bag. Find the probability that the ball drawn is 

(i) black

(ii) not black.

Solution:

(i) Total number of possible outcomes = 3 + 4 = 7.

Number of favourable outcomes for the event E.

                              = Number of black balls = 4.

So, P(E) = $\frac{\textrm{Number of Favourable Outcomes for the Event E}}{\textrm{Total Number of Possible Outcomes}}$

             = $\frac{4}{7}$.

(ii) The event of the ball being not black = $\bar{E}$.

Hence, required probability = P($\bar{E}$)

                                        = 1 - P(E)

                                        = 1 - $\frac{4}{7}$

                                        = $\frac{3}{7}$.

4. If the probability of Serena Williams a particular tennis match is 0.86, what is the probability of her losing the match?

Solution:

Let E = the event of Serena Williams winning.

From the question, P(E) = 0.86.

Clearly, $\bar{E}$ = the event of Serena Williams losing.

So, P($\bar{E}$) = 1 - P(E) 

                            = 1 - 0.86

                            = 0.14

                            = $\frac{14}{100}$

                            = $\frac{7}{50}$.

5. Find the probability of getting 53 Sunday in a leap year.

Solution:

A leap year has 366 days. So, it has 52 weeks and 2 days.

So, 52 Sundays are assured. For 53 Sundays, one of the two remaining days must be a Sunday. 

For the remaining 2 days we can have

(Sunday, Monday), (Monday, Tuesday), (Tuesday, Wednesday), (Wednesday, Thursday), (Thursday, Friday), (Friday, Saturday), (Saturday, Sunday).

So, total number of possible outcomes = 7.

Number of favourable outcomes for the event E = 2,   [namely, (Sunday, Monday), (Saturday, Sunday)].

So, by definition: P(E) = $\frac{2}{7}$.

6. A lot of 24 bulbs contains 25% defective bulbs. A bulb is drawn at random from the lot. It is found to be not defective and it is not put back. Now, one bulb is drawn at random from the rest. What is the probability that this bulb is not defective?

Solution:

25% of 24 = $\frac{25}{100}$ × 24 = 6.

So, there are 6 defective bulbs and 18 bulbs are not defective. 

After the first draw, the lot is left with 6 defective bulbs and 17 non-defective bulbs.

So, when the second bulb is drwn, the total number of possible outcomes = 23  (= 6+ 17).

Number of favourable outcomes for the event E = number of non-defective bulbs = 17.

So, the required probability = P(E) = (\frac{17}{23}\).

The examples can help the students to practice more questions on probability by following the concept provided in the solved probability problems.

Probability

Probability

Random Experiments

Experimental Probability

Events in Probability

Empirical Probability

Coin Toss Probability

Probability of Tossing Two Coins

Probability of Tossing Three Coins

Complimentary Events

Mutually Exclusive Events

Mutually Non-Exclusive Events

Conditional Probability

Theoretical Probability

Odds and Probability

Playing Cards Probability

Probability and Playing Cards

Probability for Rolling Two Dice

Solved Probability Problems

Probability for Rolling Three Dice

9th Grade Math

From Solved Probability Problems to HOME PAGE