Empirical Probability

Definition of Empirical Probability:

The experimental probability of occurring of an event is the ratio of the number of trials in which the event occurred to the total number of trials.

The empirical probability of the occurrence of an event E is defined as:

                          Number of trials in which event occurred
            ^{P(E) =}                       Total number of trials                  

If in a random experiment, n  trials are carried out and the favourable outcome for the event appears f times, the ratio \(\frac{\textit{f}}{n}\) approaches a particular value p and n becomes very large. This number p is known as the empirical probability

Let a coin be tossed several times. The number of times the head appears for every 20 trials is listed cumulatively in the following table:

---

---

Thus we see that as we go on increasing the number of trials, the value of the fraction \(\frac{\textbf{f}}{\textbf{n}}\), known as relative frequency, approaches the value 0.5, i.e., \(\frac{1}{2}\). Similarly, on several throws of a die, we find that the relative frequency of the appearance of a particular score approaches the fraction \(\frac{1}{6}\) as the number of trials increases.

Thus, from the above experimental results, empirical probability may be defined as follows:

Probability of an event E, symbolically P(E)

                                                  = \(\frac{\textrm{Frequency of the Occurrence of the Event E}}{\textrm{Sum of all the Frequencies}}\)

Note: Probability may also be found by using the following formulae:

(i) P(E) = \(\frac{\textrm{The Number of Trials in which Event E Occurs}}{\textrm{Total Number of Trials}}\)

(ii) P(E) = \(\frac{\textrm{The Number of Outcomes in Favour of the Event E}}{\textrm{Total Number of Outcomes}}\)

Now we will solve the examples on different types of experiments and their outcomes such as tossing a coin, throwing of a die etc.,

Solved Problems on Empirical Probability:

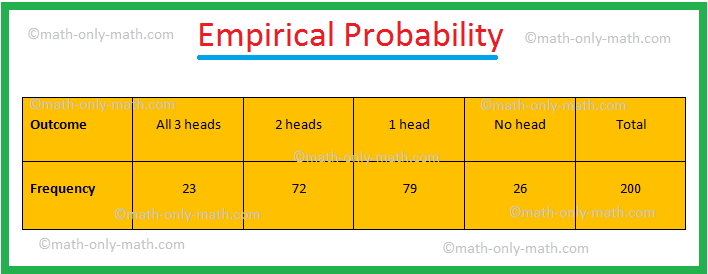
1. Three coins were tossed simultaneously 200 times and the frequencies of the different outcomes were as given in the table below:

If the three coins are again tossed simultaneously, find the probability of getting two heads.

Solution: 

Let E be the event of getting two heads.

Therefore, P(E) = \(\frac{\textrm{Frequency of getting Two Heads}}{\textrm{Sum of all the Frequencies}}\)

                    = \(\frac{72}{200}\)

                    = \(\frac{9}{25}\).

2. Let us take the experiment of tossing a coin.

When we toss a coin then we know that the results are either a head or a tail. 

Thus, in tossing a coin, all possible outcomes are ‘Head’ and ‘Tail’.

Suppose, we toss a coin 150 times and we get head, say, 102 times.

Here we will find the probability of getting:

(i) a head and,

(ii) a tail

(i) Probability of getting a head:

Let E₁ be the event of getting a head.

Then, P(getting a head)

           Number of times getting heads
^{= P(E₁) =}      Total number of trials        

= 102/150

= 0.68

(ii) Probability of getting a tail:

Total number of times a coin is tossed = 150

Number of times we get head = 102

Therefore, number of times we get tail = 150 – 102 = 48

Now, let E₂ be the event of getting a tail.

Then, P(getting a tail)

           Number of times getting tails
^{= P(E₂) =}      Total number of trials        

= 48/150

= 0.32

Note: Remember, when a coin is tossed, then E₁ and E₂ are the only possible outcomes, and P(E₁) + P(E₂) = (0.68 + 0.32) = 1

3. Consider an experiment of rolling a die.

When we roll a die then the upper face of the die are marked as 1, 2, 3, 4, 5 or 6. These are the only six possible outcomes.
Suppose we throw a die 180 times and suppose we get 5 for 72 times.

Let E = event of getting 5 (dots).

Then, clearly, P(E) = 72/180= 0.40

4. Let us take the case of tossing two coins simultaneously.

When we toss two coins simultaneously then the possible of outcomes are: (two heads) or (one head and one tail) or (two tails) i.e., in short (H,H) or (H,T) or (T,T) respectively.

Let us toss two coins randomly for 100 times.

Suppose the outcomes are:

Two heads: 35 times

One head: 30 times

0 head: 35 times

Let E₁ be the event of getting 2 heads.

Then, P(E₁) = 35/100 = 0.35

Let E₂ be the event of getting 1 head.

Then, P(E₂) = 30/100 =0.30

Let E₃ be the event of getting 0 head.

Then, P(E₃) = 35/100 = 0.35.

Note: Remember, when two coins are tossed randomly, then E₁, E₂ and E₃ are the only possible outcomes, and P(E₁) + P(E₂) + P(E₃)

= (0.35 + 0.30 + 0.35)

= 1

Probability

Probability

Random Experiments

Experimental Probability

Events in Probability

Empirical Probability

Coin Toss Probability

Probability of Tossing Two Coins

Probability of Tossing Three Coins

Complimentary Events

Mutually Exclusive Events

Mutually Non-Exclusive Events

Conditional Probability

Theoretical Probability

Odds and Probability

Playing Cards Probability

Probability and Playing Cards

Probability for Rolling Two Dice

Solved Probability Problems

Probability for Rolling Three Dice

9th Grade Math

From Empirical Probability to HOME PAGE