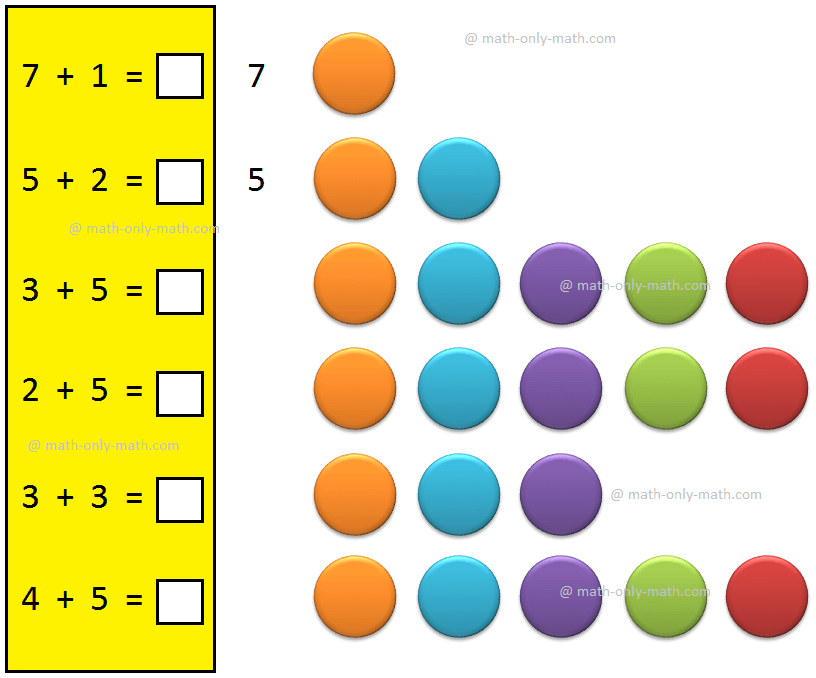Mathematics Logarithms
In mathematics logarithms were developed for making complicated calculations simple.
Definition:
Hence, if ax = M then x = loga M;
conversely, if x = loga M then ax = M.
If ‘a’ is a positive real number (except 1), n is any real number and an = b, then n is called the logarithm of b to the base a. It is written as loga b (read as log of b to the base a). Thus,
an is called the exponential form and loga b = n is called the logarithmic form.
For example:
● 32 = 9 ⇔ log3 9 = 2● 54 = 625 ⇔ log5 625 = 4
● 70 = 1 ⇔ log7 1 = 0
● 2-3 = 1/8 ⇔ log2 (1/8) = -3
● 10-2 = 0.01 ⇔ log10 0.01 = -2
● 26 = 64 ⇔ log2 64 = 6
● 3- 4 = 1/34 = 1/81 ⇔ log3 1/81 = -4
● 10-2 = 1/100 = 0.01 ⇔ log10 0.01 = -2
Notes on basic Logarithm Facts:
1. Since a > 0 (a ≠ 1), an > 0 for any rational n. Hence logarithm is defined only positive real numbers.From the definition it is clear that the logarithm of a number has no meaning if the base is not mentioned.
2. The above examples shows that the logarithm of a (positive) real number may be negative, zero or positive.
3. Logarithmic values of a given number are different for different bases.
4. Logarithms to the base a 10 are called common logarithms. Also, logarithm tables assume base 10. If no base is given, the base is assumed to be 10.
For example: log 21 means log10 21.
5. Logarithm to the base ‘e’ (where e = 2.7183 approx.) is called natural logarithm, and is usually written as ln. Thus ln x means loge x.
6. If ax = - M (a > 0, M > 0), then the value of x will be imaginary i.e., logarithmic value of a negative number is imaginary.
7. Logarithm of 1 to any finite non-zero base is zero.
Proof: We know, a0 = 1 (a ≠ 0). Therefore, from the definition, we have, loga 1 = 0.
8. Logarithm of a positive number to the same base is always 1.
Proof: Since a1 = a. Therefore, loga a = 1.
Note:
From 7 and 8 we say that, loga 1 = 0 and loga a = 1 for any positive real ‘a’ except 1.9. If x = loga M then a log a M = a
Proof: x = loga M. Therefore, ax = M or, a logaM = M [Since, x = loga M].
● Mathematics Logarithm
Convert Exponentials and Logarithms
Common Logarithm and Natural Logarithm
Logarithms
11 and 12 Grade Math
From Mathematics Logarithms to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Adding 1-Digit Number | Understand the Concept one Digit Number
Apr 26, 24 01:55 PM
Understand the concept of adding 1-digit number with the help of objects as well as numbers. -
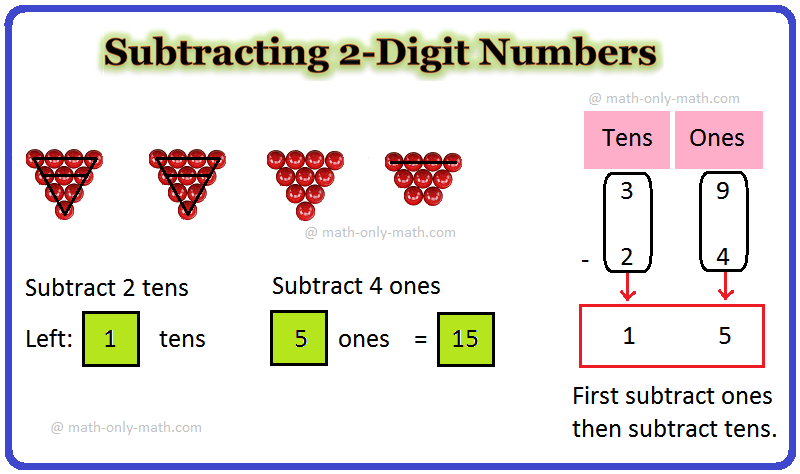
Subtracting 2-Digit Numbers | How to Subtract Two Digit Numbers?
Apr 26, 24 12:36 PM
In subtracting 2-digit numbers we will subtract or minus a two-digit number from another two-digit number. To find the difference between the two numbers we need to ‘ones from ones’ and ‘tens from -
1st Grade Word Problems on Subtraction | Subtracting 2-Digit Numbers
Apr 26, 24 12:06 PM
In 1st grade word problems on subtraction students can practice the questions on word problems based on subtraction. This exercise sheet on subtraction can be practiced by the students to get more ide… -
Subtracting 1-Digit Number | Subtract or Minus Two One-Digit Number
Apr 26, 24 11:21 AM
In subtracting 1-digit number we will subtract or minus one-digit number from one-digit number or one-digit number from 2-digit number and find the difference between them. We know that subtraction me… -
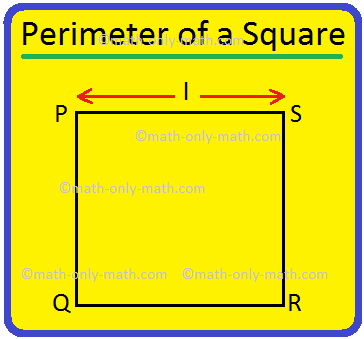
Perimeter of a Square | How to Find the Perimeter of Square? |Examples
Apr 25, 24 05:34 PM
We will discuss here how to find the perimeter of a square. Perimeter of a square is the total length (distance) of the boundary of a square. We know that all the sides of a square are equal. Perimete…