Common Logarithm and Natural Logarithm

Here we will discuss about the common logarithm and natural logarithm.
In Logarithm we have already seen and discussed that the logarithmic value of a positive number depends not only on the number but also on the base; a given positive number will have different logarithmic values for different bases.

In practice, however, following two types of logarithms are used:

    (i) Natural or Napierian logarithm 

    (ii) Common logarithm 

The logarithm of a number to the base e is known as Napierian or Natural logarithm after the name of John Napier; here the number e is an incommensurable number and is equal to the infinite series: 

    1 + ¹/₁₀ + ¹/₂₀ + ¹/₃₀ + ………… ∞

The logarithm of a number to the base 10 is known as common logarithm.

This system was first introduced by Henry Briggs. This type is used for numerical calculations. The base 10 in common logarithm is usually omitted.

For example, log₁₀ 2 is written as log 2. 

The rest of the part deals with the method of determining common logarithms of positive numbers.

Characteristic and Mantissa:

Now, consider a number (say 6.72) between 1 and 10. Clearly,

1 < 6.72 < 10

Therefore, log 1 < log 6.72 < log 10

or, 0 < log 6.72 < 1 [ Since log 1 = 0 and log 10 = 1]

Therefore, the logarithm of a number between 1 and 10 lies between 0 and 1. That is,

log 6.72 = 0 + a positive decimal part = 0∙ …………..

We now consider a number (say 58.34) between 10 and 100. Clearly,

10 < 58.34 < 100

Therefore, log 10 < log 58.34 < log 100

or, 1 < log 58.34 < 2 [Since log 10 = 1 and log 100 = 2 ]

Therefore, the logarithm of a number between 10 and 100 lies between 1 and 2. That is,

log 58.34 = 1 + a positive decimal part = 1∙ ......

Similarly, the logarithm of a number (say 463) between 100 and 1000 lies between 2 and 3 (since log 100 = 2 and log 1000 = 3). That is,

log 463 = 2 + a positive decimal part = 2∙ …….

In like manner the logarithm of a number between 1000 and 10000 lies between 3 and 4 and so on.

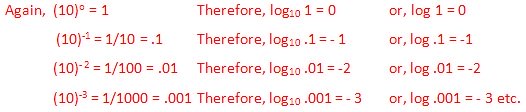
Now, consider a number (say .54) between 1 and .1. Clearly,

.1 < .54 < 1

Therefore, log .1 < log .54 < log 1

or, - 1 < log .54 < 0, [Since log 1 = 0 and log .1 = - 1]

Therefore, the logarithm of a number between .1 and 1 lies between - 1 and 0. That is,

log .54 = -0∙ ……. = - 1 + a positive decimal part.

We now consider a number (say .0252 ) between .1 and ∙01. Clearly,

.01 < .0252 < .1

log 0.1 < log .0252 < log .1

or, -2 < log .0252 < - 1 [since log .1 = - 1 and log .01 = -2]

Therefore, the logarithm of a number between .01 and .1 lies between -2 and - 1 . That is,

log .0252 = - 1∙ ..... = - 2+ a positive decimal part.

Similarly, the logarithm of a number between .001 and .01 lies between - 3 and -2 and so on.

From the above discussions it is observed that the common logarithm of a positive number consists of two parts. One part is integral which may be zero or any integer (positive or negative) and the other part is non-negative decimal.


The integral part of a common logarithm is called the characteristic and the non-negative decimal part is called the mantissa.

Suppose, log 39.2 = 1.5933, then 1 is the characteristic and 5933 is the mantissa of the logarithm.

If log .009423 = - 3 + .9742, then - 3 is the characteristic and .9742 is the mantissa of the logarithm.

Since log 3 = 0.4771 and log 10 = 1, so the characteristic of log 3 is 0 and the mantissa of log 10 is 0.

Determination of Characteristic and Mantissa:

The characteristic of the logarithm of a number is determined by inspection and the mantissa by logarithmic table.

(i) To find the characteristic of the logarithm of a number greater than 1:

Since, log 1 = 0 and log 10 = 1 , hence the common logarithm of a number between 1 and 10 (i.e., whose integral part consists of one digit only) lies between 0 and 1.

For example, each of the numbers 5, 8.5, 9.64 lies between 1 and 10 (see that the integral part of each of them consists of one digit only); hence their logarithms lie between 0 and 1 i.e.,

log 5 = 0 + a positive decimal part = 0∙ ……

log 8.5 = 0 + a positive decimal part = 0∙ …..

log 9.64 = 0 + a positive decimal part = 0∙ …..

Therefore, the characteristic of each of log 5, log 8.5 or log 9.64 is 0.

Again, the common logarithm of a number whose integral part consists of two digits only (i.e., of a number between 10 and 100) lies between 1 and 2 (log 10 = 1 and log 100 = 2).

For example, the integral part of each of the numbers 36, 86.2, 90.46 consists of two digits; hence their logarithms lie between 1 and 2, i.e.,

log 36 = 1 + a positive decimal part = 1∙ ……

log 86.2 = 1 + a positive decimal part = 1∙ ……

log 90.46 = 1 + a positive decimal part = 1∙ ……

Therefore, the characteristic of each of log 36, log 86.2 or log 90.46 is 1.

Similarly, the characteristic of the logarithm of a number whose integral part consists of 3 digits is 2. In general, the characteristic of the logarithm of a number whose integral part consists of n digits is n - 1. Accordingly, we have the following rule:

The characteristic of the logarithm of a number greater than 1 is positive and is one less than the number of digits in the integral part of the number.

Example:

(ii) To find the characteristic of the logarithm of a number lying between 0 and 1:

Since, log .1 = -1 and log 1 = 0, hence the common logarithm of a number between .1 and 1 lies between -1 and 0. For example, each of .5, .62 or .976 lies between .1 and 1; hence their logarithms lie between -1 and 0, i.e.,

log .5 = -0∙ ..... = -1 + a positive decimal part = 1∙ …..

log .62 = -0∙ …. = -1 + a positive decimal part = 1∙ …..

log .976 = -0∙ ….. = - 1 + a positive decimal part = 1∙ …..

[See that a number between (- 1) and 0 is of the form (-0∙ …… ), such as (-0.246),
(-0.594) etc. But (- 0.246) can be expressed as follows:

- 0.246 = -1 + 1 -0.246 = -1 + 0.754 = -1+ a positive decimal part.

It is the convension to represent the mantissa of the logarithm of a number as positive.

For this reason a number lying between (- 1) and 0 is expressed in the above form.

Again, (-1) + .754 is written as 1.754. Clearly, the integral part in1.754 is negative [i.e., (- 1)] but the decimal part is positive. 1.754 is read as bar 1 point 7, 5, 4. Note that, (-1.754) and (1.754) are not the same. 1.754 = - 1 + .754 but (-1.754) = - 1 - .754]

Therefore, the characteristic of each of log .5, log .62 or log .976 is (- 1).

Again, a number having one zero between the decimal sign and the first significant figure lies between .0l and .1. Hence, its logarithm will lie between (-2) and (- 1) [Since, log .01 = - 2 and log .1 = - 1].

For example, each of .04, .056, .0934 lies between .01 and .1 (see that there is one zero between the decimal sign and the first significant digit in all the numbers) hence, their logarithms will lie between (-2) and (- 1), i.e., 

log .04 = - 1∙ ……. = -2 + a positive decimal part = 2∙ ………….

log .056 = -1∙ ……. = -2 + a positive decimal part = 2∙ …………..

1og.0934= -1∙ ……. = -2 + a positive decimal part = 2∙ …………..

Similarly, the characteristic of the logarithm of a number having two zeroes between the decimal sign and the first significant figure is (- 3). In general, the characteristic of the logarithm of a number having n zeroes between the decimal sign and the first significant figure is - (n + 1).

Accordingly, we have the following rule:

The characteristic of the logarithm of a positive number less than 1 is negative and is numerically greater by 1 than the number of zeroes between the decimal sign and the first significant figure of the number.

Example:

(iii) To find the mantissa [using log-table]:

After determining the characteristic of the logarithm of a positive number by inspection, its mantissa is determined by the logarithmic table. At the end of the book both four-figure and five-figure tables are given. A four-figure table gives the value of mantissa correct to 4 decimal places.

Similarly, a five-figure or a nine-figure log-table gives the value of mantissa correct to five or nine decimal places. Using any one of them we can find the mantissa f the common logarithm of a number lying between 1 to 9999, If the number contains more than 4 significant digits then to find the mantissa by the table either we can approximate it upto 4 significant figures for rough calculations or else we can utilize the principle of proportional parts for more precise calculations. In tables mantissa correct to certain places of decimals are given without the decimal point. It should be remembered that the mantissa of common logarithm of a number is independent of the position of the decimal point in the number. In fact, the decimal point of the number is discarded when the mantissa is determined by the log-table.

For example, the mantissa of each of the numbers 6254, 625.4, 6.254 or, 0.006254 is the same.

Observing the log-table given at the end of the book we see that it is divided into following four parts:

  (a) in the extreme left-hand column numbers ranging from 10 to 99;

  (b) numbers ranging from 0 to 9 in the top-most row;

  (è) four-digit numbers (in a four-figure log-table) below each figure of the top-most row;

  (d) mean difference column.

Suppose we are to find the mantissa of (i) log 6 (ii) log 0.048 (iii) log 39.2 and (iv) log 523.4 by log-table.

(i) log 6

Since mantissa of log 6 and log 600 are same, we shall have to see the mantissa of log 600. Now we find the figure 60 in the column of part (a) of the table; next we move horizontally to the right to the column headed by 0 of part (b) and read the number 7782 in part (c) of the table (see four-figure log-table). Thus the mantissa of log 6 is .7782.


(ii) log 0.048

Since the mantissa of common logarithm is independent of the position of the decimal point, hence to find the mantissa of log 0.048 we shall find the mantissa of log 480. As in (i) we first-find the figure 48 in the column of part (a) of the table ; next we move horizontally to the right to the column headed by 0 of part (b) and read the number 6812 in part (c) of the table. Thus the mantissa of log 0.048 is .6812.


(iii) log 39.2

Similarly, to find the mantissa of log 39.2 we shall find the mantissa of log 392. As in (i), we find the figure 39 in the column of part (a); next we move horizontally to the right to the column headed by 2 of part (b) and read the number 5933 in part (c) of the table. Thus the mantissa of log 39.2 is .5933


(iv) log 523.4

In like manner we first discard the decimal point in 523.4. Now we find the figure 52 in the column of part (a); next we move horizontally to the right to the column headed by 3 of part (b) and read the number 7185 in part (c) of the table. Again we move along the same horizontal line further right to the column headed by 4 of mean difference and read the number 3 there. If this 3 be added with 7185, then we shall get the mantissa of log 523.4. Thus the mantissa of log 523.4 is .7188.

Note:

Clearly, the characteristics of log 6, log 0.048, log 39.2 and log 523.4 are 0, (-2), 1 and 2 respectively.

Hence, we have,

log 6 = 0.7782,

log 0.048 = 2.68l2,

log 39.2 = 1.5933 and

log 523.4 = 2.7188.

● Mathematics Logarithm

Mathematics Logarithms

Convert Exponentials and Logarithms

Logarithm Rules or Log Rules

Solved Problems on Logarithm

Common Logarithm and Natural Logarithm

Antilogarithm

11 and 12 Grade Math 

Logarithm 

From Common Logarithm and Natural Logarithm to HOME PAGE