Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Home | About Us | Contact Us | Privacy | Math Blog
Binary Numbers
In binary numbers system first we will discuss about the;
Data are a
collection of facts and figures which act as a raw material for information.
The processed data which help to make decisions or further manipulations are
called information.
The total number of symbols used in a particular number system is called base or radix and each symbol is called a digit. The decimal number system has base 10 and the digits are 0, 1, 2, 3, 4, 5, 5, 6, 7, 8, 9.
To binary number system have base 2 and the binary digits 0 and 1. BIT is a contraction of the world’s BInary digiT.
Electronic and electrical components of a computer are bistable in nature. The binary digit 0 and 1 are most suitable and are conveniently used to express the two possible status. Internal circuit designs of a computer become simplified as the circuits have to handle only two bits instead of ten digits of the decimal system. Also all the operations that can be done in decimal system can also is done in binary system.
Conversion of number from one system to another is necessary to understand the logic and process of operations. Binary numbers can be easily converted to decimal numbers and vice versa. Conversion of binary numbers to decimal numbers can be conveniently accomplished by either actual expansion method or by value box method. Similarly decimal numbers may be converted to binary numbers either by value box method or by multiplication and division method.
Octal and hexadecimal number systems are also used in digital computers. Octal number system has a base 8 and the symbols used are 0, 1, 2, 3, 4, 5, 6, 7. Hexadecimal number system has a base 16 and the symbols used are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Conversion of binary numbers to octal or hexadecimal numbers and vice versa can also be easily accomplished.
Addition, subtraction, multiplication and division of binary number system can be made by following the usual rules of arithmetic.
- Why Binary Numbers are Used
- Binary to Decimal Conversion
- Conversion of Numbers
- Hexa-decimal Number System
- Conversion of Binary Numbers to Octal or Hexa-decimal Numbers
- Octal and Hexa-Decimal Numbers
- Signed-magnitude Representation
- Radix Complement
- Diminished Radix Complement
- Arithmetic Operations of Binary Numbers
From Binary Numbers to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Worksheet on Area, Perimeter and Volume | Square, Rectangle, Cube,Cubo
Jul 25, 25 12:21 PM
In this worksheet on area perimeter and volume you will get different types of questions on find the perimeter of a rectangle, find the perimeter of a square, find the area of a rectangle, find the ar… -
Worksheet on Volume of a Cube and Cuboid |The Volume of a RectangleBox
Jul 25, 25 03:15 AM
We will practice the questions given in the worksheet on volume of a cube and cuboid. We know the volume of an object is the amount of space occupied by the object.1. Fill in the blanks: -
Volume of a Cuboid | Volume of Cuboid Formula | How to Find the Volume
Jul 24, 25 03:46 PM
Cuboid is a solid box whose every surface is a rectangle of same area or different areas. A cuboid will have a length, breadth and height. Hence we can conclude that volume is 3 dimensional. To measur… -
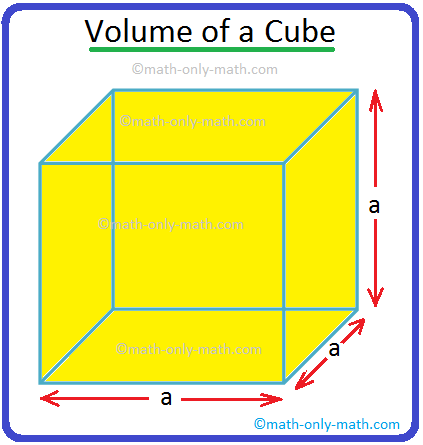
Volume of a Cube | How to Calculate the Volume of a Cube? | Examples
Jul 23, 25 11:37 AM
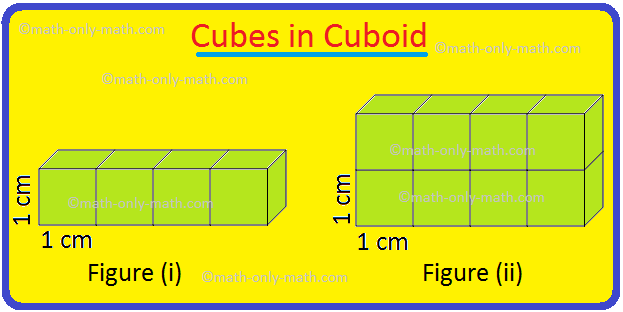
A cube is a solid box whose every surface is a square of same area. Take an empty box with open top in the shape of a cube whose each edge is 2 cm. Now fit cubes of edges 1 cm in it. From the figure i… -
5th Grade Volume | Units of Volume | Measurement of Volume|Cubic Units
Jul 20, 25 10:22 AM
Volume is the amount of space enclosed by an object or shape, how much 3-dimensional space (length, height, and width) it occupies. A flat shape like triangle, square and rectangle occupies surface on…



New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.