Octal Number System
Octal number system has a base or radix 8. Eight different symbols, namely 0, 1, 2, 3, 4, 5, 6, 7 are used to represent octal numbers. Conversion of octal numbers to their decimal equivalents can be accomplished by using the same rule which was followed to convert binary numbers to decimal numbers, except that we now have a radix 8 instead of 2. Thus the octal number 273 has the decimal equivalent.
2738
= 2 × 82 + 7 × 81 + 3 × 80
= 128 + 56 + 3
= 18710
Conversion of decimal I integers to octal can be performed by successively dividing number by 8 and using each remainder as a digit of the desired octal number. We note that the first remainder is the least significant digit and the last one is the most significant digit. In the case of decimal fractions, we use the same method which was used in converting decimal fractions to binary fractions.
Few examples on octal number system are explained with this method:
Convert the decimal numbers to their octal equivalents:
(a) 2980
Solution:
2980
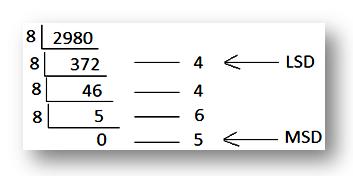
Hence 298010 = 56448
(b) 0.685
Solution:
0.685
Decimal Numbers to Binary Number Conversion Table |
|||||||
|---|---|---|---|---|---|---|---|
| Multiplication | Integer | Fraction | |||||
| 0.685 × 8 = 5.480 | 5 | .48 | |||||
| 0.48 × 8 = 3.84 | 3 | .84 | |||||
| .84 × 8 = 6.72 | 6 | .72 | |||||
| .72 × 8 = 5.76 | 5 | .76 | |||||
Therefore, 0.68510 = (0.5365…)8
`
From Octal Number System to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
|
|
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.