Perimeter of a Rectangle
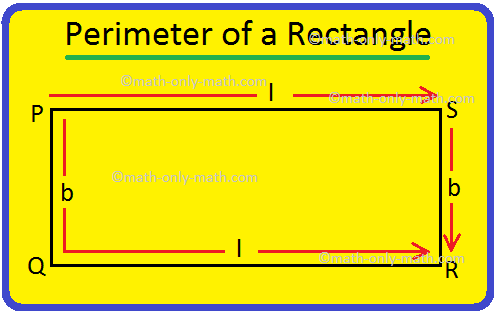
We will discuss here how to find the perimeter of a rectangle. We know perimeter of a rectangle is the total length (distance) of the boundary of a rectangle.
In a rectangle we know that two opposite sides are equal. So, PQ = SR and PS = QR
If PS = l and PQ = b
Perimeter of the rectangle = PQ + QR + RS + SP
= b +l + b + l
= 2b +2l
Again,
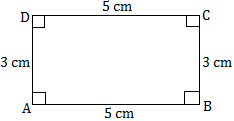
ABCD is a rectangle. We know that the opposite sides of a rectangle are equal.
AB = CD = 5 cm and BC = AD = 3 cm
So, the perimeter of the rectangle ABCD = AB + BC + CD + AD = 5 cm + 3 cm + 5 cm + 3 cm = 16 cm
It can be written as 5 cm + 5 cm + 3 cm + 3 cm
= (2 × 5) cm + (2 × 3) cm
= 2 (5 + 3) cm
= 2 × 8 cm
= 16 cm
We add length and breadth twice to find the perimeter of a rectangle.
Perimeter of a rectangle = 2 (length + breadth)
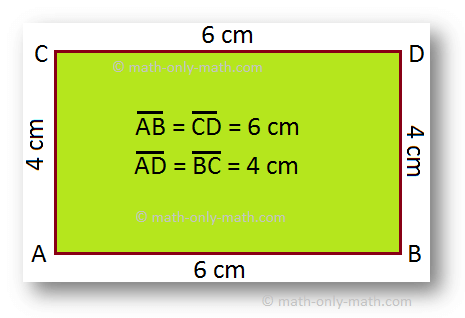
A rectangle is a four sided figure in which
● Opposite sides are equal in length.
● Longer side is called length and shorter side is called breadth.
● All angles are equal to 90° (right angle).
In the above figure ABCD is a rectangle.
Three children found the perimeter of this rectangle in three different methods.
1st method:
Perimeter = 6 cm + 4 cm + 6 cm + 4 cm = 20 cm
2nd method:
Perimeter = (2 6 cm) + (2 4 cm) = 12 cm + 8 cm = 20 cm
3rd method:
Perimeter = 2 (6 cm + 4 cm) = 2 cm × 10 cm = 20 cm
All the three methods gave them the same answer.
Perimeter of a rectangle = length + breadth + length + breadth
= (2 length) + (2 breadth)
= 2 (length + breadth)
Word Problems on Perimeter of a Rectangle:
Let us consider some of the examples on perimeter of a rectangle:
1. The length of a rectangle is 4 cm and its breadth is 2 cm. Find its perimeter.
Solution:
Length = 4 cm
Breadth = 2 cm
Therefore, perimeter of the rectangle
= 2 (length + breadth)
= 2 (4 + 2) cm
= 2 × 6 cm
= 12 cm
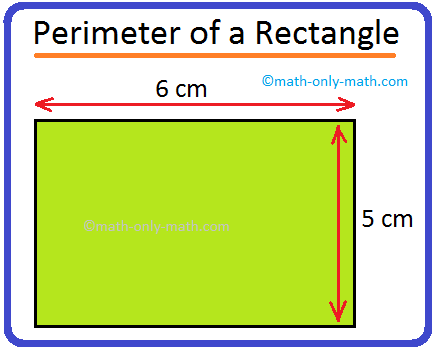
2. Find the perimeter of the rectangle ABCD whose sides are 6 cm and 5 cm.
Solution:
The perimeter of the rectangle ABCD
= 6 cm + 5 cm + 6 cm + 5cm
= 22 cm
3. Find the perimeter of a rectangle whose length is 12 cm and breadth is 8 cm.
Solution:
Length = 12 cm
Breadth = 8 cm
Perimeter = 2 (length + breadth)
= 2 (12 cm + 8 cm)
= 2 × 20 cm
= 40 cm
4. A rectangular swimming pool is 9 m long and 4 m broad. Find the area of the swimming pool.
Solution:
Length of the rectangular swimming pool = 9 m
Breadth of the rectangular swimming pool = 4 m
Therefore, perimeter of the rectangle swimming pool
= 2 (length + breadth)
= 2 (9 + 4) m
= 2 (13) m
= 2 × 13 m
= 26 m
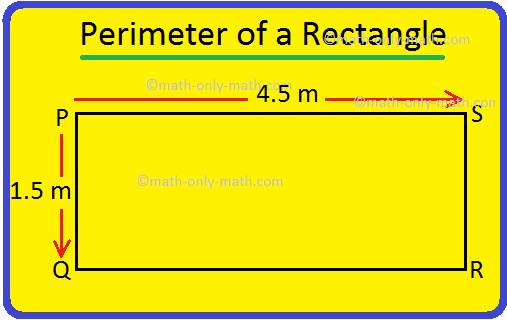
5. The length of a rectangle is 4.5 m and the breadth is 1.5 m. Find the perimeter.
Solution:
Length = 4.5 m
Breadth = 1.5 m
Perimeter = 2 (length + breadth)
= 2 × (4.5 m + 1.5 m)
= 2 × 6 m
= 12 m
Therefore, the perimeter is 12 m.
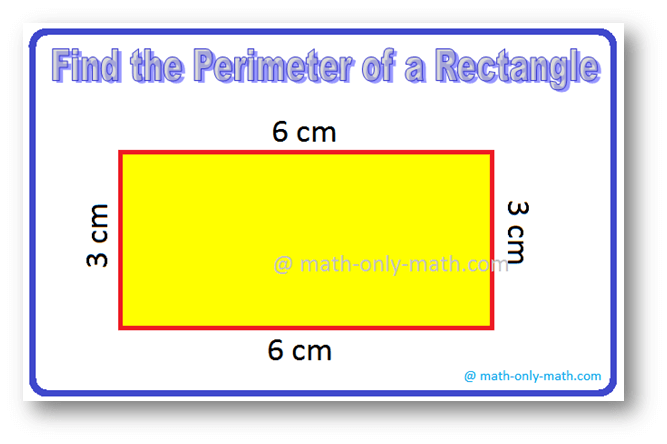
6. How to find the perimeter of a rectangle?
Find the perimeter of the given figure.
Solution:
A rectangle has four sides.
To find the perimeter of a rectangle, we measure all the four sides of the figure and add them together.
In the above given figure, length of the 4 sides are = 6 cm, 3 cm, 6 cm, 3 cm.
Therefore, perimeter of the square = 6 cm + 3 cm + 6 cm + 3 cm
= 18 cm
7. A rectangle display board is measuring 8 m by 6 m. Robert wants to add a ribbon border around the display board. What is the length of ribbon that he will need? If the cost of the ribbon is $ 15 per metre then how much money does Robert needs to buy the ribbon?
Solution:
Length of the display board = 8 m
Breadth of the display board = 6 m
Perimeter of the display board = 2 (Length + Breadth)
= 2 (8 + 6) m
= 2 × 14 m
= 28 m.
Cost of ribbon is $15 per meter.
Therefore, total cost for 28 m long ribbon = $15 × 28
= $420.
Worksheet on Perimeter of a Rectangle:
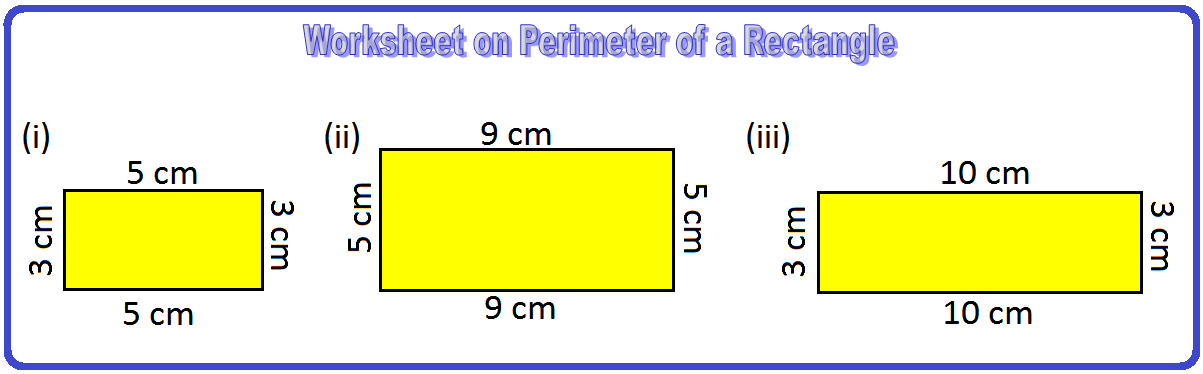
1. Find the perimeter of the rectangles having measurements as follows.
(i) length = 11 cm breadth = 9 cm
(ii) length = 5 cm breadth = 2 cm
(iii) length = 10 cm breadth = 8 cm
(iv) length = 15 cm breadth = 2 cm
Answer:
1. (i) 40 cm
(ii) 14 cm
(iii) 36 cm
(iv) 34 cm
Perimeter of a Rectangle Word Problems
2. A rectangle has a perimeter of 40 cm. If its length is 8 cm, what is its breath?
Answer:
2. 12 cm
3. Sam is running around a rectangular park of length 450 m and breadth 300 m. Find the total distance covered by him if he takes 10 rounds of the park.
Answer:
3. 15000 m
4. A gardener wants to fence its rectangular garden with a wire. The length and breadth of the garden is 25 m and 16 m respectively. Find the length of the wire he must buy.
Answer:
4. 82 m
5. Find the perimeter of each of the following rectangles using formula:
Answer:
5. (i) Perimeter of the rectangle 16 cm.
(ii) Perimeter of the rectangle 28 cm.
(iii) Perimeter of the rectangle 26 cm.
You might like these
Different Types of Polygons | Triangle, Quadrilateral|Pentagon|Hexagon
The different types of polygons are discussed here. In any polygon a pair of sides that are inclined to each other meet at a point. This point is called a vertex of the polygon. In the polygon there
What is a Quadrilateral? | Symbol of a Quadrilateral □ | Rectangle
What is a quadrilateral? A simple closed curve or a polygon formed by four line-segments is called a quadrilateral.
Classification of Angles | Types of Angles | Acute, Right, Obtuse, ...
Classification of angles on the basis of their degree measures are given below: Acute angle: An angle whose measure is more than 0° but less than 90° is called an acute angle. Angles having mag
Measuring an Angle | Using Protractor | Comparison of Angles | Example
We will discuss here about measuring an angle with the help of a protractor. You can find it in your Geometry Box. It has the semi-circular shape. Its semi-circular edge is divided
Comparing Different Line Segments | Difference of two line segments
We will discuss here about comparing different line segments. Different line segments can be of different lengths. We can compare the lengths of the different line segments
Circle Math | Parts of a Circle | Terms Related to the Circle | Symbol
In circle math the terms related to the circle are discussed here. A circle is such a closed curve whose every point is equidistant from a fixed point called its centre. The symbol of circle is O. We have learned to draw a circle, by tracing the outlines of objects like a
What is a Triangle? | Types of Triangle | Scalene Triangle | Isosceles
A simple closed curve or a polygon formed by three line-segments (sides) is called a triangle. The above shown shapes are triangles. The symbol of a triangle is ∆. A triangle is a polygon with three sides. In the given figure ABC is a triangle. AB, BC and CA are its sides.
What is a Polygon? | Simple Closed Curve | Triangle | Quadrilateral
What is a polygon? A simple closed curve made of three or more line-segments is called a polygon. A polygon has at least three line-segments.
Simple Closed Curves | Types of Closed Curves | Collection of Curves
In simple closed curves the shapes are closed by line-segments or by a curved line. Triangle, quadrilateral, circle, etc., are examples of closed curves.
Measuring the Line Segment | Comparing Line Segments
We will discuss here about measuring the line segment i.e. how to draw and measure a line segment using scale or ruler. We can measure a line segment by two ways. (i) With the help of scale
Perimeter of a Square | How to Find the Perimeter of Square? |Examples
We will discuss here how to find the perimeter of a square. Perimeter of a square is the total length (distance) of the boundary of a square. We know that all the sides of a square are equal. Perimeter of a Square Perimeter of the square ABCD = AB+BC+CD+AD=2 cm+2cm+2cm+2cm
Perimeter of a Triangle | Perimeter of a Triangle Formula | Examples
We will discuss here how to find the perimeter of a triangle. We know perimeter of a triangle is the total length (distance) of the boundary of a triangle. Perimeter of a triangle is the sum of lengths of its three sides. The perimeter of a triangle ABC Perimeter
Symmetrical Shapes | One, Two, Three, Four & Many-line Symmetry
Symmetrical shapes are discussed here in this topic. Any object or shape which can be cut in two equal halves in such a way that both the parts are exactly the same is called symmetrical. The line which divides the shape is called the symmetry. So, if we place a mirror
Mental Math on Geometrical Shapes | Geometry Worksheets| Answer
In mental math on geometrical shapes we will solve different type of problems on simple closed curves, polygons, basic geometrical concepts, perpendicular lines, parallel lines, circle, terms relates to circle, relation between radius and diameter of a circle, symmetry
● Related Concepts
● To Measure the Length of a Line-segment
● Examples on Unit of Mass or Weight
● Units for The Measurement of Capacity
● Examples on Measurement of Capacity
● Antemeridian (a.m.) or Postmeridian (p.m.)
● Calendar
● Reading and Interpreting a Calendar
From Perimeter of a Rectangle to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Word Problems on Area and Perimeter | Free Worksheet with Answers
Jul 26, 24 04:58 PM
word problems on area and perimeter -
Worksheet on Perimeter | Perimeter of Squares and Rectangle | Answers
Jul 26, 24 04:37 PM
Practice the questions given in the worksheet on perimeter. The questions are based on finding the perimeter of the triangle, perimeter of the square, perimeter of rectangle and word problems. I. Find… -
Perimeter and Area of Irregular Figures | Solved Example Problems
Jul 26, 24 02:20 PM
Here we will get the ideas how to solve the problems on finding the perimeter and area of irregular figures. The figure PQRSTU is a hexagon. PS is a diagonal and QY, RO, TX and UZ are the respective d… -
Perimeter and Area of Plane Figures | Definition of Perimeter and Area
Jul 26, 24 11:50 AM
A plane figure is made of line segments or arcs of curves in a plane. It is a closed figure if the figure begins and ends at the same point. We are familiar with plane figures like squares, rectangles… -
5th Grade Math Problems | Table of Contents | Worksheets |Free Answers
Jul 26, 24 01:35 AM
In 5th grade math problems you will get all types of examples on different topics along with the solutions. Keeping in mind the mental level of child in Grade 5, every efforts has been made to introdu…
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.