Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Examples on Unit of Mass or Weight
Here are some solved examples on unit of mass or weight which help us to understand measurement of mass.
Consider the following examples on unit of mass or weight:
1. Change (1) 7165 kg into quintal and (ii) 345 quintal into kg.
Solution:
(i) 7165 kg = ? quintal
Since 100 kg = 1 quintal
Therefore, 7165 kg = 7165 kg ÷ 100 kg
= 71 quintal 65 kg
Therefore 7165 kg = 71 quintal 65 kg and
(ii) 345 quintal = ? kg
Since 1 quintal = 100 kg
Therefore, 345 q = 345 x 100
= 34500 kg
Therefore 345 quintal = 34500 kg
2. Add the following:
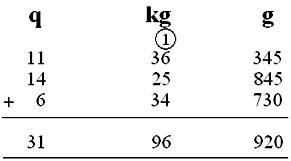
11 q 36 kg 345g, 14 q 25 kg 845g, 6 q 34 kg 730g
Solution:
(i) g column is added
345 + 845 + 730 = 1920 g
= 1 kg 920 g
(ii) kg column is added
1 + 36 + 25 + 34 = 96 kg
(iii) q column is added
11 + 14 + 6 = 31 q
= 31 q 96 kg 920 g
3. David is 9kg heavier than Mike who weighs 35kg 675g. What is the weight of David?
Solution:
David’s weight = 35 kg 675g + 9kg = 44 kg 675 g
4. A fruit-seller bought 46kg 500g of mangoes from one garden,
75kg 750g of mangoes from another garden and 64kg 250g of mangoes from
the third garden. How much mangoes were bought by the fruit-seller? If
he sold 75kg 750g mangoes, how much mangoes has he now?
Solution:
Mangoes bought from one garden = 46 kg 500 g
Mangoes bought from another garden = 75 kg 750 g
Mangoes bought from third garden = + 64 kg 250 g
Total = 186 kg 500 g
Mangoes sold = - 75 kg 750 g
Mangoes left with fruit-seller = 110 kg 750 g
5. The cost of 1 kg of tomatoes is $20.00. What is the cost of (i) 5 kg, (ii) 500 g, (iii) 100 g of tomatoes?
Solution:
(i) Since the cost of 1 kg of tomatoes = $20.00
Therefore the cost of 5 kg of tomatoes = 5 x $20 = $100
(ii) The cost of 500 g or 1/2 kg of tomatoes = 1/2 x $20 = $10
(iii) The cost of 100 g of tomatoes = 100/1000 x $20 = $2
Hence,
(i) 5 kg tomatoes cost $100
(ii) 500 g tomatoes cost $10
(iii) 100 g tomatoes cost $2
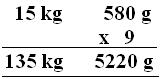
6. A tin of ghee weighs 15 kg 580 g. What will be the weight of (i) 9, (ii) 40 such tins?
Solution:
(i) Weight of 1 tin of ghee = 15 kg 580 g
Therefore weight of 9 tins of ghee = 9 x 15 kg 580 g
= 135 kg + 5 kg + 220 g
= 140 kg 220 g
(ii) Weight of 40 tins of ghee = 15 kg 580 g x 40
= 600 kg + 23 kg + 200 g
= 623 kg 200 g
7. The cost of 1 kg of apples is $40. What is the cost of 250 g of apples?
Solution:
250 g = 1/4 of 1000 g or 1/4 of 1 kg
Hence, cost of 250 g = 1/4 cost of 1 kg
= $40 ÷ 4
= $10
Hence, cost of 250 g of apples = $10
Related Concepts
● To Measure the Length of a Line-segment
● Examples on Unit of Mass or Weight
● Units for The Measurement of Capacity
● Examples on Measurement of Capacity
● Antemeridian (a.m.) or Postmeridian (p.m.)
● Calendar
● Reading and Interpreting a Calendar
4th Grade Math Activities
From Examples on Unit of Mass or Weight to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
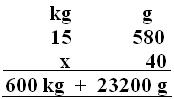


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.