Trigonometrical Ratios of Complementary Angles

How to find the trigonometrical ratios of complementary angles?

If the sum of two angles is one right angle or 90°, then one angle is said to be complementary of the other. Thus, 25° and 65°; θ° and (90 - θ)° are complementary to each other.

Suppose a rotating line rotates about O in the anti-clockwise sense and starting from its initial position

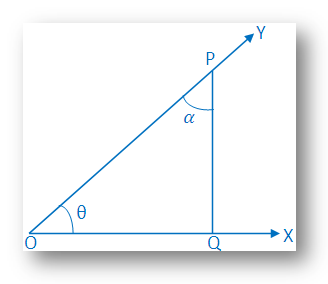
$\overrightarrow{OX}$ traces out angle ∠XOY = θ, where θ is acute. 

Take a point P on $\overrightarrow{OY}$  and draw $\overline{PQ}$  perpendicular to OX.  Let, ∠OPQ = α. Then, we have,

α + θ = 90°

or, α = 90° -  θ.

Therefore, θ and α are complementary to each other.

Now, by the definition of trigonometric ratio,

sin θ = $\frac{\overline{PQ}}{\overline{OP}}$; ………. (i)

cos θ = $\frac{\overline{OQ}}{\overline{OP}}$; ………. (ii)

tan θ = $\frac{\overline{PQ}}{\overline{OQ}}$ ………. (iii)

And   sin α = $\frac{\overline{OQ}}{\overline{OP}}$; ………. (iv)

cos α = $\frac{\overline{PQ}}{\overline{OP}}$; ………. (v)

tan α = $\frac{\overline{OQ}}{\overline{PQ}}$  ….… (vi)

From (i) and (iv) we have,

sin α = cos θ   

or,  sin (90° -  θ) = cos θ;

From (ii) and (v) we have,

cos α = sin θ   

or, cos (90° -  θ) = sin θ;

From (iii) and (vi) we have,

And tan α = 1/tan θ

or, tan (90° - θ) = cot θ.

Similarly, csc (90° - θ) = sec θ;

sec (90° - θ) = csc θ

and cot (90° - θ) = tan θ.

Therefore,

Sine of any angle    = cosine of its complementary angle;

Cosine of any angle = sine of its complementary angle;

Tangent of any angle = cotangent of its complementary angle.

Corollary:

Complementary Angles: Two angles are said to be complementary if their sum is 90°. Thus θ and (90° - θ) are complementary angles.

We know there are six trigonometrical ratios in trigonometry. The above explanation will help us to find the trigonometrical ratios of complementary angles.

Worked-out problems on trigonometrical ratios of complementary angles:

1. Without using trigonometric tables, evaluate $\frac{tan  65°}{cot  25°}$

Solution:

$\frac{tan  65°}{cot  25°}$

= $\frac{tan  65°}{cot (90°  -  65°)}$

=  $\frac{tan   65°}{tan  65°}$, [Since cot (90° -  θ) = tan θ]

= 1

2. Without using trigonometric tables, evaluate sin 35° sin 55° - cos 35° cos 55°

Solution:

sin 35° sin 55° - cos 35° cos 55°

= sin 35° sin (90° - 35°) - cos 35° cos (90° - 35°),

= sin 35° cos 35° - cos 35° sin 35°,

                                      [Since sin (90° -  θ) = cos θ and cos (90° -  θ) = sin θ]

= sin 35° cos 35° - sin 35° cos 35°

= 0

3.  If sec 5θ = csc (θ - 36°), where 5θ is an acute angle, find the value of θ.

Solution:

    sec 5θ = csc (θ - 36°)

⇒ csc (90° - 5θ) = csc (θ - 36°), [Since sec θ = csc (90° -  θ)]

⇒ (90° - 5θ) = (θ - 36°)

⇒ -5θ - θ = -36° - 90°

⇒ -6θ = -126°

⇒ θ = 21°, [Dividing both sides by -6]

Therefore, θ = 21°

4. Using trigonometrical ratios of complementary angles prove that tan 1° tan 2° tan 3° ......... tan 89° = 1

Solution:

   tan 1° tan 2° tan 3° ...... tan 89°

= tan 1° tan 2° ...... tan 44° tan 45° tan 46° ...... tan 88° tan 89°

= (tan 1° ∙ tan 89°) (tan 2° ∙ tan 88°) ...... (tan 44° ∙ tan 46°) ∙ tan 45°

= {tan 1° ∙ tan (90° - 1°)} ∙ {tan 2° ∙ (tan 90° - 2°)} ...... {tan 44° ∙ tan (90° - 44°)} ∙ tan 45°

= (tan 1° ∙ cot 1°)(tan 2° ∙ cot 2°) ...... (tan 44° ∙ cot 44°) ∙ tan 45°, [Since tan (90° - θ) = cot θ]

= (1)(1) ...... (1) ∙ 1, [since tan θ ∙ cot θ = 1 and tan 45° = 1]

= 1

Therefore, tan 1° tan 2° tan 3° ...... tan 89° = 1

● Trigonometric Functions

• Basic Trigonometric Ratios and Their Names
• Restrictions of Trigonometrical Ratios
• Reciprocal Relations of Trigonometric Ratios
• Quotient Relations of Trigonometric Ratios
  
• Limit of Trigonometric Ratios
  
• Trigonometrical Identity
• Problems on Trigonometric Identities
• Elimination of Trigonometric Ratios
• Eliminate Theta between the equations
• Problems on Eliminate Theta
• Trig Ratio Problems
• Proving Trigonometric Ratios
• Trig Ratios Proving Problems
• Verify Trigonometric Identities
• Trigonometrical Ratios of 0°
• Trigonometrical Ratios of 30°
• Trigonometrical Ratios of 45°
• Trigonometrical Ratios of 60°
• Trigonometrical Ratios of 90°
• Trigonometrical Ratios Table
• Problems on Trigonometric Ratio of Standard Angle
  
• Trigonometrical Ratios of Complementary Angles
• Rules of Trigonometric Signs
• Signs of Trigonometrical Ratios
  
• All Sin Tan Cos Rule
• Trigonometrical Ratios of (- θ)
• Trigonometrical Ratios of (90° + θ)
• Trigonometrical Ratios of (90° - θ)
• Trigonometrical Ratios of (180° + θ)
• Trigonometrical Ratios of (180° - θ)
• Trigonometrical Ratios of (270° + θ)
• Trigonometrical Ratios of (270° - θ)
• Trigonometrical Ratios of (360° + θ)
• Trigonometrical Ratios of (360° - θ)
• Trigonometrical Ratios of any Angle
• Trigonometrical Ratios of some Particular Angles
• Trigonometric Ratios of an Angle
• Trigonometric Functions of any Angles
• Problems on Trigonometric Ratios of an Angle
• Problems on Signs of Trigonometrical Ratios

11 and 12 Grade Math

From Trigonometrical Ratios of Complementary Angles to HOME PAGE