Straight Line in Intercept Form

We will learn how to find the equation of a straight line in intercept form.

The equation of a line which cuts off intercepts a and b respectively from the x and y axes is $\frac{x}{a}$ + $\frac{y}{b}$ = 1.

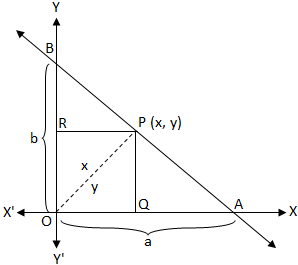
Let the straight line AB intersects the x-axis at A and the y-axis at B where OA = a and OB = b.

Straight Line in Intercept Form

Now we have to find the equation of the straight line AB.

Let P(x, y) be any point on the line AB. Draw PQ perpendicular on OX and PR perpendicular on OX. Then, join the points O and P. Now, PQ = y, OQ = x.

Clearly, we see that

Area of the ∆OAB = Area of the ∆OPA + Area of the ∆OPB

⇒ ½ OA ∙ OB = ½ ∙ OA ∙ PQ + ½ ∙ OB ∙ PR

⇒ ½ a ∙ b = ½ ∙ a ∙ y + ½ ∙ b ∙ x

⇒ ab = ay + bx

⇒ $\frac{ab}{ab}$ = $\frac{ay + bx}{ab}$, dividing both sides by ab

⇒ 1 = $\frac{ay}{ab}$ + $\frac{bx}{ab}$

⇒ 1 = $\frac{y}{b}$ + $\frac{x}{a}$

⇒ $\frac{x}{a}$ + $\frac{y}{b}$ = 1, which is the equation of the line in the intercept form.

The equation $\frac{x}{a}$ + $\frac{y}{b}$ = 1 is the satisfied by the co-ordinates of any point P lying on the line AB.

Therefore, $\frac{x}{a}$ + $\frac{y}{b}$ = 1 represent the equation of the straight line AB.

Solved examples to find the equation of a straight line in intercept form:

1. Find the equation of the line which cuts off an intercept 3 on the positive direction of x-axis and an intercept 5 on the negative direction of y-axis.

Solution: 

The equation of a line which cuts off intercepts a and b respectively from the x and y axes is $\frac{x}{a}$ + $\frac{y}{b}$ = 1.

Here, a = 3 and b = -5

Therefore, the equation of the straight line is $\frac{x}{a}$ + $\frac{y}{b}$ = 1 ⇒ $\frac{x}{3}$ + $\frac{y}{-5}$ = 1 ⇒ $\frac{x}{3}$ - $\frac{y}{5}$ = 1 ⇒ 5x – 3y = 15 ⇒ 5x – 3y – 15 = 0.

2. Find the intercepts of the straight line 4x + 3y = 24 on the co-ordinate axes.

Solution:

Given equation 4x + 3y = 24.

Now convert the given equation into intercept form.

4x + 3y = 24

⇒ $\frac{4x + 3y}{24}$ = $\frac{24}{24}$, Dividing both sides by 24

⇒ $\frac{4x}{24}$ + $\frac{3y}{24}$ = 1

⇒ $\frac{x}{6}$ + $\frac{y}{8}$ = 1, which is the intercept form.

Therefore, x-intercept = 6 and y-intercept = 8.

Note: (i) The straight line $\frac{x}{a}$ + $\frac{y}{b}$ = 1 intersects the x-axis at A(a, 0) and the y-axis at B(0, b).

(ii) In $\frac{x}{a}$ + $\frac{y}{b}$ = 1, a is x-intercept and b is y- intercept.

These intercept a and b may be positive as well as negative.

(iii) If the straight line AB passing through the origin then, a = 0 and b = 0. If we put a = 0 and b = 0 in the intercept form, then $\frac{x}{0}$ + $\frac{y}{0}$ = 1, which is undefined. For this reason the equation of a straight line passing through the origin cannot be expressed in the intercept form.

(iv) A line parallel to the x-axis does not intercept the x-axis at any finite distance and hence, we cannot get any finite x- intercept (i.e., a) of such a line. For this reason, a line parallel to x-axis cannot be expressed in the intercept from. In like manner, we cannot get any finite y- intercept (i.e., b) of a line parallel to y-axis and hence, such a line cannot be expressed in the intercept form.

● The Straight Line

• Straight Line
• Slope of a Straight Line
• Slope of a Line through Two Given Points
• Collinearity of Three Points
• Equation of a Line Parallel to x-axis
• Equation of a Line Parallel to y-axis
• Slope-intercept Form
• Point-slope Form
• Straight line in Two-point Form
• Straight Line in Intercept Form
• Straight Line in Normal Form
• General Form into Slope-intercept Form
• General Form into Intercept Form
• General Form into Normal Form
  
• Point of Intersection of Two Lines
  
• Concurrency of Three Lines
• Angle between Two Straight Lines
• Condition of Parallelism of Lines
• Equation of a Line Parallel to a Line
• Condition of Perpendicularity of Two Lines
• Equation of a Line Perpendicular to a Line
• Identical Straight Lines
• Position of a Point Relative to a Line
• Distance of a Point from a Straight Line
• Equations of the Bisectors of the Angles between Two Straight Lines
• Bisector of the Angle which Contains the Origin
• Straight Line Formulae
• Problems on Straight Lines
• Word Problems on Straight Lines
• Problems on Slope and Intercept

11 and 12 Grade Math

From Straight Line in Intercept Form to HOME PAGE