Position of a Point Relative to a Line

We will learn how to find the position of a point relative to a line and also the condition for two points to lie on the same or opposite side of a given straight line.

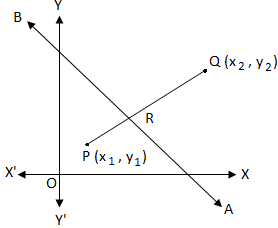
Let the equation of the given line AB be ax + by + C = 0…………….(i) and let the coordinates of the two given points P (x\(_{1}\), y\(_{1}\)) and Q (x\(_{2}\), y\(_{2}\)).

I: When P and Q are on opposite sides:

Let us assumed that the points P and Q are on opposite sides of the straight line.

The coordinate of the point R which divides the line joining P and Q internally in the ratio m : n are

(\(\frac{mx_{2} + nx_{1}}{m + n}\), \(\frac{my_{2} + ny_{1}}{m + n}\))

Since the point R lies on ax + by + C = 0 hence we must have,

a ∙ \(\frac{mx_{2} + nx_{1}}{m + n}\) + b ∙ \(\frac{my_{2} + ny_{1}}{m + n}\) + c = 0

⇒ amx\(_{2}\) + anx\(_{1}\) + bmy\(_{2}\) + bny\(_{1}\) + cm + cn = 0

⇒ m(ax\(_{2}\) + by\(_{2}\) + c )= - n(ax\(_{1}\) + by\(_{1}\) + c)  

⇒ \(\frac{m}{n} = - \frac{ax_{1} + by_{1} + c}{ax_{2} + by_{2} + c}\)………………(ii)

II: When P and Q are on same sides:

Let us assumed that the points P and Q are on same side of the straight line. Now join P and Q. Now assume that the straight line, (produced) intersects at R.

The coordinate of the point R which divides the line joining P and Q externally in the ratio m : n are

(\(\frac{mx_{2} - nx_{1}}{m - n}\), \(\frac{my_{2} - ny_{1}}{m - n}\))

Since the point R lies on ax + by + C = 0 hence we must have,

a ∙ \(\frac{mx_{2} - nx_{1}}{m - n}\) + b ∙ \(\frac{my_{2} - ny_{1}}{m - n}\) + c = 0

⇒ amx\(_{2}\) - anx\(_{1}\) + bmy\(_{2}\) - bny\(_{1}\) + cm - cn = 0

⇒ m(ax\(_{2}\) + by\(_{2}\) + c )= n(ax\(_{1}\) + by\(_{1}\) + c)  

⇒ \(\frac{m}{n} = \frac{ax_{1} + by_{1} + c}{ax_{2} + by_{2} + c}\)………………(iii)

Clearly, \(\frac{m}{n}\) is positive; hence, the condition (ii) is satisfied if (ax\(_{1}\)+ by\(_{1}\) + c) and (ax\(_{2}\) + by\(_{2}\) + c) are of opposite signs. Therefore, the points P (x\(_{1}\), y\(_{1}\)) and Q (x\(_{2}\), y\(_{2}\)) will be on opposite sides of the straight line ax + by + C = 0 if(ax\(_{1}\)+ by\(_{1}\) + c) and (ax\(_{2}\) + by\(_{2}\) + c) are of opposite signs.

Again, the condition (iii) is satisfied if (ax\(_{1}\)+ by\(_{1}\) + c) and (ax\(_{2}\) + by\(_{2}\) + c) have the same signs. Therefore, the points P (x\(_{1}\), y\(_{1}\)) and Q (x\(_{2}\), y\(_{2}\)will be on the same side of the line ax + by + C = 0 if (ax\(_{1}\)+ by\(_{1}\) + c) and (ax\(_{2}\) + by\(_{2}\) + c) have the same signs.

Thus, the two points P (x\(_{1}\), y\(_{1}\)) and Q (x\(_{2}\), y\(_{2}\)) are on the same side or opposite sides of the straight line ax + by + c = 0, according as the quantities (ax\(_{1}\)+ by\(_{1}\) + c) and (ax\(_{2}\) + by\(_{2}\) + c) have the same or opposite signs.

Remarks: 1. Let ax + by + c = 0 be a given straight line and P (x\(_{1}\), y\(_{1}\)) be a given point. If ax\(_{1}\)+ by\(_{1}\) + c is positive, then the side of the straight line on which the point P lies is called the positive side of the line and the other side is called its negative side.

2. Since a ∙ 0 + b ∙ 0 + c = c, hence it is evident that the origin is on the positive side of the line ax + by + c = 0 when c is positive and the origin is on the negative side of the line when c is negative.

3. The origin and the point P (x\(_{1}\), y\(_{1}\)) are on the same side or opposite sides of the straight line ax + by + c = 0, according as c and (ax\(_{1}\)+ by\(_{1}\) + c) are of the same or opposite signs.

 

Solved examples to find the position of a point with respect to a given straight line:

1. Are the points (2, -3) and (4, 2) on the same or opposite sides of the line 3x - 4y - 7 = 0?

Solution:

Let Z = 3x - 4y - 7.

Now the value of Z at (2, -3) is

Z\(_{1}\) (let) =3 × (2) - 4 × (-3) - 7

= 6 + 12 - 7

= 18 - 7

= 11, which is positive.

Again, the value of Z at (4, 2) is

Z\(_{2}\) (let) = 3 × (4) - 4 × (2) - 7

= 12 - 8 - 7

= 12 - 15

= -3, which is negative.

Since, z\(_{1}\) and z\(_{2}\), are of opposite signs, therefore the two points (2, -3) and (4, 2) are on the opposite sides of the given line 3x - 4y - 7 = 0.

2. Show that the points (3, 4) and (-5, 6) lie on the same side of the straight line 5x - 2y = 9.

Solution: 

The given equation of the straight line is 5x - 2y = 9.

⇒ 5x - 2y - 9 = 0 ……………………… (i)

Now find the value of 5x - 2y - 9 at (3, 4)

Putting x = 3 and y = 4 in the expression 5x - 2y - 9 we get,

5 × (3) - 2 × (4) - 9 = 15 - 8 - 9 = 15 - 17 = -2, which is negative.

Again, putting x = 5 and y = -6 in the expression 5x - 2y - 9 we get,

5 × (-5) - 2 × (-6) - 9 = -25 + 12 - 9 = -13 - 9 = -32, which is negative.

Thus, the value of the expression 5x - 2y - 9 at (2, -3) and (4, 2) are of same signs. Therefore, the given two points (3, 4) and (-5, 6) lie on the same side of the line given straight line 5x - 2y = 9.

● The Straight Line

• Straight Line
• Slope of a Straight Line
• Slope of a Line through Two Given Points
• Collinearity of Three Points
• Equation of a Line Parallel to x-axis
• Equation of a Line Parallel to y-axis
• Slope-intercept Form
• Point-slope Form
• Straight line in Two-point Form
• Straight Line in Intercept Form
• Straight Line in Normal Form
• General Form into Slope-intercept Form
• General Form into Intercept Form
• General Form into Normal Form
  
• Point of Intersection of Two Lines
  
• Concurrency of Three Lines
• Angle between Two Straight Lines
• Condition of Parallelism of Lines
• Equation of a Line Parallel to a Line
• Condition of Perpendicularity of Two Lines
• Equation of a Line Perpendicular to a Line
• Identical Straight Lines
• Position of a Point Relative to a Line
• Distance of a Point from a Straight Line
• Equations of the Bisectors of the Angles between Two Straight Lines
• Bisector of the Angle which Contains the Origin
• Straight Line Formulae
• Problems on Straight Lines
• Word Problems on Straight Lines
• Problems on Slope and Intercept

11 and 12 Grade Math

From Position of a Point Relative to a Line to HOME PAGE