Subscribe to our ▶️YouTube channel🔴 for the latest videos, updates, and tips.
Home | About Us | Contact Us | Privacy | Math Blog
Condition of Perpendicularity of Two Lines
We will learn how to find the condition of perpendicularity of two lines.
If two lines AB and CD of slopes m1 and m2 are perpendicular, then the angle between the lines θ is of 90°.
Therefore, cot θ = 0
⇒ 1+m1m2m2−m1 = 0
⇒ 1 + m1m2 = 0
⇒ m1m2 = -1.
Thus when two lines are perpendicular, the product of their slope is -1. If m is the slope of a line, then the slope of a line perpendicular to it is -1/m.
Let us assume that the lines y = m1x + c1 and y = m2 x + c2 make angles α and β respectively with the positive direction of the x-axis and θ be the angle between them.
Therefore, α = θ + β = 90° + β [Since, θ = 90°]
Now taking tan on both sides we get,
tan α = tan (θ + β)
tan α = - cot β
tan α = - 1tanβ
or, m1 = - 1m1
or, m1m2 = -1
Therefore, the condition of perpendicularity of the lines y = m1x + c1, and y = m2 x + c2 is m1m2 = -1.
Conversely, if m1m2 = - 1 then
tan ∙ tan β = - 1
sinαsinβcosαcosβ = -1
sin α sin β = - cos α cos β
cos α cos β + sin α sin β = 0
cos (α - β) = 0
Therefore, α - β = 90°
Therefore, θ = α - β = 90°
Thus, the straight lines AB and CD are perpendicular to each other.
Solved examples to find the condition of perpendicularity of two given straight lines:
1. Let P (6, 4) and Q (2, 12) be the two points. Find the slope of a line perpendicular to PQ.
Solution:
Let m be the slope of PQ.
Then m = 12−42−6 = 8−4 = -2
Therefore the slope of the line perpendicular to PQ = - 1m = ½
2. Without using the Pythagoras theorem, show that P (4, 4), Q (3, 5) and R (-1, -1) are the vertices of a right angled triangle.
Solution:
In ∆ ABC, we have:
m1 = Slope of the side PQ = 4−54−3 = -1
m2 = Slope of the side PR = 4−(−1)4−(−1) = 1
Now clearly we see that m1m2 = 1 × -1 = -1
Therefore, the side PQ perpendicular to PR that is ∠RPQ = 90°.
Therefore, the given points P (4, 4), Q (3, 5) and R (-1, -1) are the vertices of a right angled triangle.
3. Find the ortho-centre of the triangle formed by joining the points P (- 2, -3), Q (6, 1) and R (1, 6).
Solution:
The slope of the side QR of the ∆PQR is 6−11−6 = 5−5 = -1∙
Let PS be the perpendicular from P on QR; hence, if the slope of the line PS be m then,
m × (- 1) = - 1
or, m = 1.
Therefore, the equation of the straight line PS is
y + 3 = 1 (x + 2)
or, x - y = 1 …………………(1)
Again, the slope of the side RP of the ∆ PQR is 6+31+2 = 3∙
Let QT be the perpendicular from Q on RP; hence, if the slope of the line QT be m1 then,
m1 × 3 = -1
or, m1 = -13
Therefore, tile equation of the straight line QT is
y – 1 = -13(x - 6)
or, 3y – 3 = - x + 6
Or, x + 3y = 9 ………………(2)
Now, solving equations (1) and (2) we get, x = 3, y = 2.
Therefore, the co-ordinates of the point of intersection of the lines (1) and (2) are (3, 2).
Therefore, the co-ordinates of the ortho-centre of the ∆PQR = the co-ordinates of the point of intersection of the straight lines PS and QT = (3, 2).
● The Straight Line
- Straight Line
- Slope of a Straight Line
- Slope of a Line through Two Given Points
- Collinearity of Three Points
- Equation of a Line Parallel to x-axis
- Equation of a Line Parallel to y-axis
- Slope-intercept Form
- Point-slope Form
- Straight line in Two-point Form
- Straight Line in Intercept Form
- Straight Line in Normal Form
- General Form into Slope-intercept Form
- General Form into Intercept Form
- General Form into Normal Form
- Point of Intersection of Two Lines
- Concurrency of Three Lines
- Angle between Two Straight Lines
- Condition of Parallelism of Lines
- Equation of a Line Parallel to a Line
- Condition of Perpendicularity of Two Lines
- Equation of a Line Perpendicular to a Line
- Identical Straight Lines
- Position of a Point Relative to a Line
- Distance of a Point from a Straight Line
- Equations of the Bisectors of the Angles between Two Straight Lines
- Bisector of the Angle which Contains the Origin
- Straight Line Formulae
- Problems on Straight Lines
- Word Problems on Straight Lines
- Problems on Slope and Intercept
11 and 12 Grade Math
From Condition of Perpendicularity of Two Lines to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
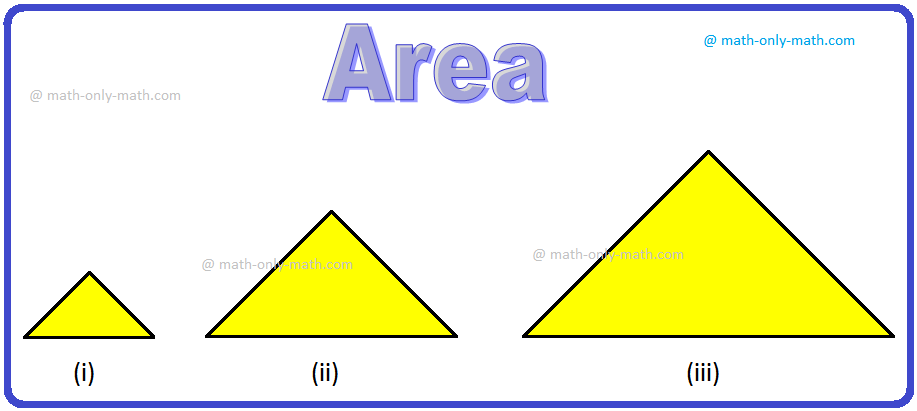
Area of Rectangle Square and Triangle | Formulas| Area of Plane Shapes
Jul 18, 25 10:38 AM
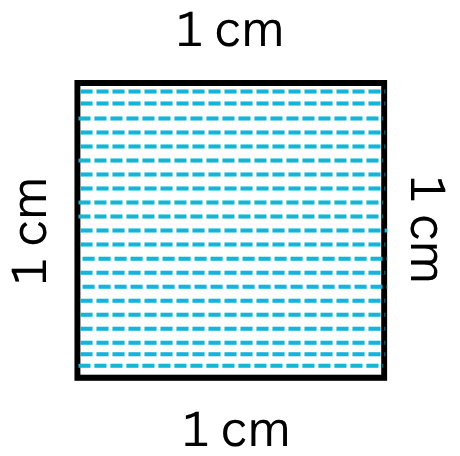
Area of a closed plane figure is the amount of surface enclosed within its boundary. Look at the given figures. The shaded region of each figure denotes its area. The standard unit, generally used for… -
What is Area in Maths? | Units to find Area | Conversion Table of Area
Jul 17, 25 01:06 AM
The amount of surface that a plane figure covers is called its area. It’s unit is square centimeters or square meters etc. A rectangle, a square, a triangle and a circle are all examples of closed pla… -
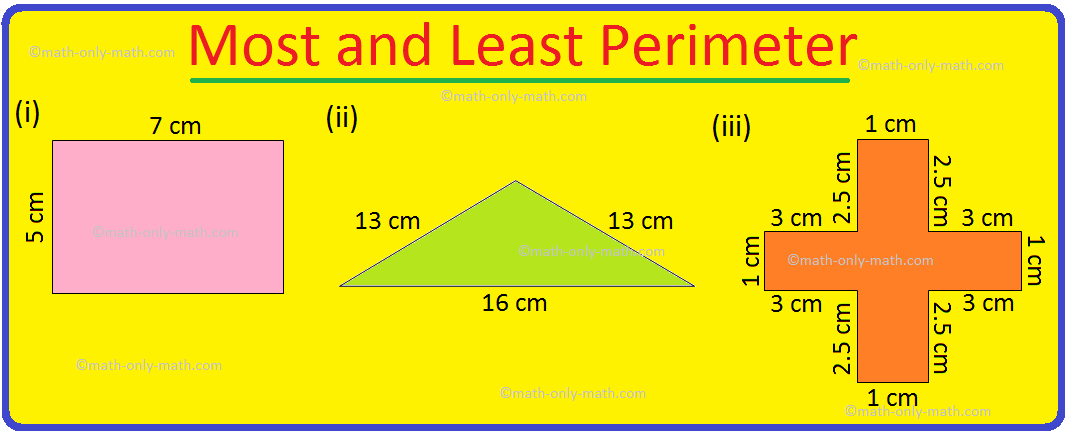
Worksheet on Perimeter | Perimeter of Squares and Rectangle | Answers
Jul 17, 25 12:40 AM
Practice the questions given in the worksheet on perimeter. The questions are based on finding the perimeter of the triangle, perimeter of the square, perimeter of rectangle and word problems. I. Find… -
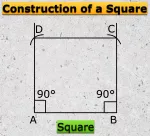
Formation of Square and Rectangle | Construction of Square & Rectangle
Jul 16, 25 11:46 PM
In formation of square and rectangle we will learn how to construct square and rectangle. Construction of a Square: We follow the method given below. Step I: We draw a line segment AB of the required… -
Perimeter of a Figure | Perimeter of a Simple Closed Figure | Examples
Jul 16, 25 02:33 AM
Perimeter of a figure is explained here. Perimeter is the total length of the boundary of a closed figure. The perimeter of a simple closed figure is the sum of the measures of line-segments which hav…

New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.