Conversion of Rupees and Paise

We will discuss about the conversion of rupees and paise (i.e. conversion from rupees to paise and conversion from paise to rupees).

We know that 20 rupees is written as ₹20.

Also, 50 paise is written as 50 p.

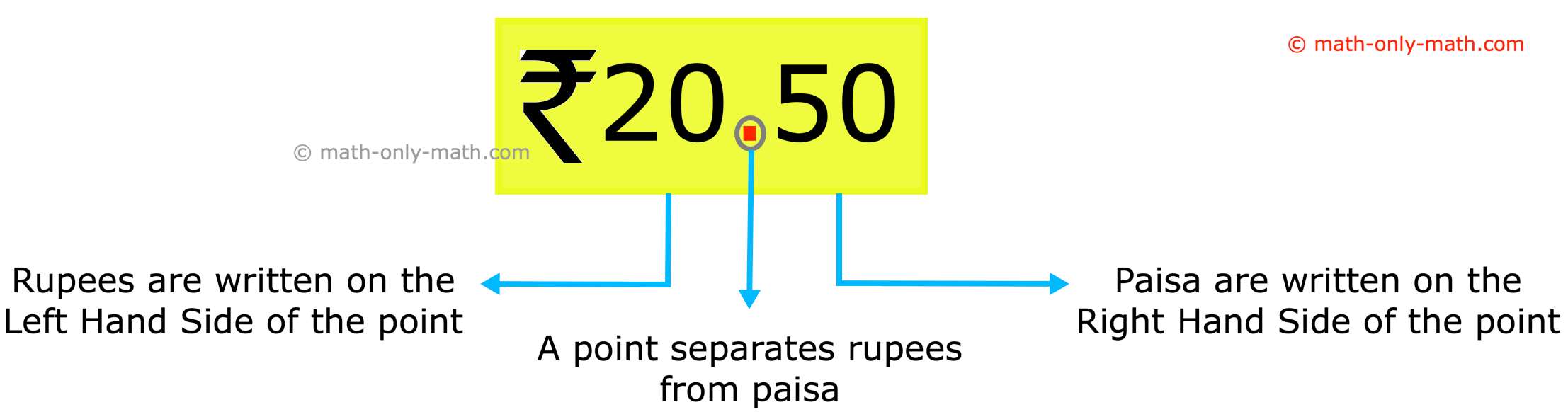
But, how do we write 20 rupees 50 paise?

For writing rupees and paise together, we use a point.

20 rupees 50 paise is written as shown below.

RUPEES AND PAISE

We know that, ₹ 1 = 100 paise

For example;

Convert ₹ 5 and ₹ 12 into paise.

₹ 5 = 5 × 100 = 500 paise

₹ 12 = 12 × 100 = 1200 paise

How to convert rupees into paise?

Process 1:

A very simple rule to convert rupees into paise  or rupees and paise into paise is to remove the symbol ₹ and / or the dot or point  (.) as the case may be and write paise (p) at the right end of the number.

For example, to convert ₹ 4.25 into paise we express it as 425 paise.

Consider some of the following examples on convert rupees into paise:

(i) ₹ 0.60 = 60 paise

(ii) ₹ 11.05 = 1105 paise

(iii) ₹ 14.00 = 1400 paise

(iv) Convert ₹ 12.40 into paise.

To convert this into paise, simply remove the symbol and then the point and write the paise at the end.

So, ₹ 12.40 = 1240 p

More examples on converting rupees and paise into paise:

1. ₹ 3 into paise.

= 3 × 100 paise = 300 paise

So,  ₹ 3 = 300 p

2. ₹ 9.00 = 900 p

3. ₹ 15.75 = 1575 p

4. ₹ 83.35 = 8335 p

5. ₹ 215.70 = 21570 p

Process 2: (using process 2 we will solve the same examples of process 1)

We know that 1 rupee = 100 paise. When we convert rupees and paise into paise, we multiply the number of rupees by 100 and then we add the existing paise to the product.

For example, ₹ 4.25 = ₹ 4 + 25 paise

                                = 4 × 100 paise + 25 paise

                                = 400 paise + 25 paise

                                = 425 paise

Consider some of the following examples on Convert Rupees into Paise:

To convert rupees and paise into paise, we multiply the rupees by 100 and then add the existing paise to the product.

(i) ₹ 0.60 = ₹ 0 + 60 paise

                 = 0 × 100 paise + 60 paise

                 = 0 paise + 60 paise

                 = 60 paise

(ii) ₹ 11.05 = ₹ 11 + 05 paise

                   = 11 × 100 paise + 05 paise

                   = 1100 paise + 05 paise

                   = 1105 paise                                      

(iii) ₹ 14.00  = ₹ 14 + 00 paise

                     = 14 × 100 paise + 00 paise

                     = 1400 paise + 00 paise

                     = 1400 paise

(iv) ₹ 12.40 into paise.

Solution:

Amount in words - Twelve rupees and forty paise

12 × 100 paise + 40 paise = 1240 paise

So, ₹ 12.40 = 1240 p

More examples on converting rupees and paise into paise:

1. Convert ₹ 18.25 into paise.

Solution:

= ₹ 18 + 25 p

= 18 × 100 p + 25 p

= 1800 p + 25 p

= 1825 p

2. Convert ₹ 464.80 into paise.

Solution:

 ₹ 464.80 = ₹ 464 + 80 p

               = 464 × 100 p +80 p

               = 46400 p + 80 p

               = 46480 p

3. Convert ₹ 4.25 into paise.

Solution:

4.25 = 4 × 100p + 25p

       = (400 + 25) p

       = 425 p

Therefore, ₹ 4.25 = 425 p

How to convert paise into rupees?

First Method: To convert paise into rupees or rupees and paise, first we need to count two digits from the right of the given number showing paise and put a point (.) and also put the symbol ₹ in the beginning.

Consider some of the following examples:

(i) 335 p = 330 p + 35 p

                = ₹ 3 and 35 p or ₹ 3.35

(ii) 4,286 p = 4,200 p + 86 p

                 = ₹ 42 and 86 p or ₹ 42.86

(iii) 1250 p = ₹ 12.50

(iv) 705 p = ₹ 7.05

(v) 30 p = ₹ 0.30

(vi) 9,495 p = ₹ 94.95

(vii) 12,835 = ₹ 128.35

Second Method: To convert paise into rupees, we divide it by 100. We will simply put a dot (.) before the second digit from the right to convert the paise.

 Consider some of the following examples:

1. Convert 4356 paise into rupees.

Solution:

To convert it into rupees, we will simply put a dot (.) before the second digit from the right.

4356 paise = ₹ 43.56 or 43 rupees and 56 paise.

2. Convert 321 paise into rupees.

Solution:

To convert it into rupees, we will simply put a dot (.) before the second digit from the right.

321 paise = ₹ 3.21 or 3 rupees and 21 paise.

3. Convert 3200 paise into rupees.

Solution:

To convert it into rupees, we will simply put a dot (.) before the second digit from the right.

3200 paise = ₹ 32.00 or 32 rupees.

4. Convert 750 paise into rupees.

Solution:

750 paise = (100 + 100 + 100 + 100 + 100 + 100 + 100 + 50) Paise

              = ₹ 7 + 50 p     [Since, paise = ₹ 1]

              = ₹ 7.50 100 

Therefore, 750 paise = ₹ 7.50.

Mental Maths on Conversion of Rupees and Paise:

1. Write the following in rupees and paise.

(i) ₹ 0.25 = __________

(ii) ₹ 0.05 = __________

Answer:

1. (i) 25 p

(ii) 5 p

Related Concepts

Money

Coins and Currency Notes

Writing Money in Words and Figure

Conversion of Money

Conversion of Rupees and Paise

Addition of Money

Subtraction of Money

Multiplication of Money

Division of Money

3rd Grade Math Worksheets

3rd Grade Math Lessons

From Conversion of Rupees and Paise to HOME PAGE