Pairs of Angles

Pairs of angles are discussed here in this lesson. Some angles are given special names because of their positions.

1. Complementary Angles:

Two angles whose sum is 90° (that is, one right angle) are called complementary angles and one is called the complement of the other.

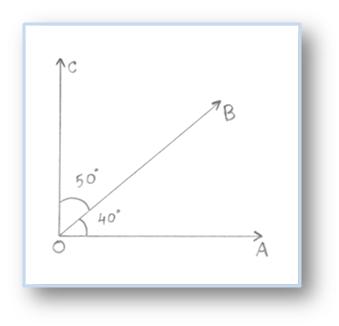
Here, ∠AOB = 40° and ∠BOC = 50°

Therefore, ∠AOB + ∠BOC = 90°

Here, ∠AOB and ∠BOC are called complementary angles.

∠AOB is complement of ∠BOC and ∠BOC is complement of ∠AOB.

Definition of Complementary Angles:

Two angles are said to be complementary, if the sum of their measures is 90°.

Note: Complementary angles need not be adjacent. It is only the sum of their measures that determines whether they are complementary or not.

Examples of Adjacent Angles:

(i) An angle of 50° is complementary to another angle of measure 40°. Each angle is said to be the complement of the other.

(ii) Angles of measure 60° and 30° are complementary angles because 60° + 30° = 90°

Thus, the complementary angle of 60° is the angle measure 30°. The complementary angle angle of 30° is the angle of measure 60°.

(iii) Complement of 30° is → 90° - 30° = 60°

(iv) Complement of 45° is → 90° - 45° = 45°

(v) Complement of 55° is → 90° - 55° = 35°

(vi) Complement of 75° is → 90° - 75° = 15°

Solved Examples of Adjacent Angles:

1. 42° and 48° form a pair of complementary angles. Is this statement true? Give reason.

Solution:

Yes, the statement is true, because 42° + 48° = 90° and two angles are said to be complementary if the sum of their measures is 90°.

Working Rules to Find the Complementary Angles: To find the complementary angle of a given angle subtract the measure of an angle from 90°.

So, the complementary angle = 90° - the given angle.

2. Supplementary Angles:

Two angles whose sum is 180° (that is, one straight angle) are called supplementary angles and one is called the supplement of the other.

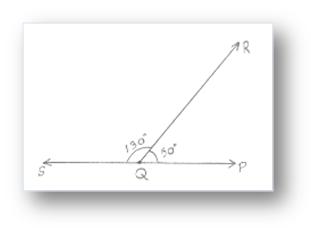
Here, ∠PQR = 50° and ∠RQS = 130°

∠PQR + ∠RQS = 180° Hence, ∠PQR and ∠RQS are called supplementary angles and ∠PQR is 

supplement of ∠RQS and ∠RQS is supplement of ∠PQR.

Definition of Supplementary Angles:

Two angles are said to be supplementary, if the sum of their measures is 180°.

Examples of Supplementary Angles:

(i) The two angles measuring 120° and 60° are supplementary to each other. Each angle is said to be the supplement of the other.

(ii) Angles of measure 100° and 80° are supplementary angles because 100° + 80° = 180°.

Thus the supplementary angle of 80° is the angle of measure 100°.

(iii) Supplement of - 55° is 180° - 55° = 125°

(iv) Supplement of 95° is 180° - 95° = 85°

(v) Supplement of 135° is 180° - 135° = 45°

(vi) Supplement of 150° is 180° - 150° = 30°

Solved Example on Supplementary Angles:

1. 80° and 100° form a pair of supplementary angles. Is the statement correct? Give reason.

Solution:

Yes, the statement is true, because 80° + 100° = 180° and two angles are said to be supplementary if the sum of their measures is 180°.

Working Rules to Find the Supplementary Angles: To find the supplementary angle of a given angle, subtract the measure of angle from 180°.

So, the supplementary angle = 180° - the given angle.

Note:

1. The two angles which form a linear pair are always supplementary.

2. Like complementary angles, the supplementary angles need not be adjacent.

3. Adjacent Angles:

Two non – overlapping angles are said to be adjacent angles if they have:

(a) a common vertex

(b) a common arm

(c) other two arms lying on opposite side of this common arm, so that their interiors do not overlap.

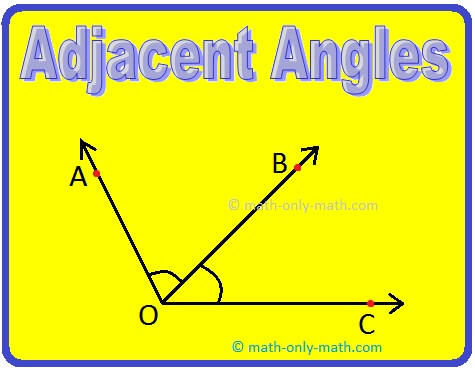
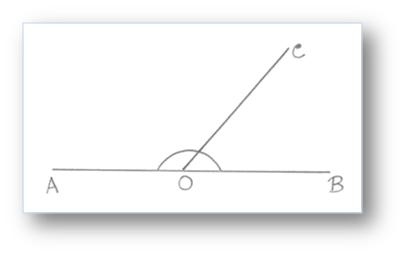
In the above given figure, ∠AOB and ∠BOC are non – overlapping, have OB as the common arm and O as the common vertex. The other arms OC and OA of the angles ∠BOC and ∠AOB are an opposite sides, of the common arm OB.

Hence, the arm ∠AOB and ∠BOC form a pair of adjacent angles.

Definition of Adjacent Angles:

Two angles are said to be adjacent, if they have a common vertex and a common arm. The other two arms extend on opposite sides of the common arms.

In figure, ∠AOB and ∠BOC are adjacent. They have a common vertex O and common arm OB. The other two arms OA and OC are called the outer arms.

Examples of Adjacent Angles:

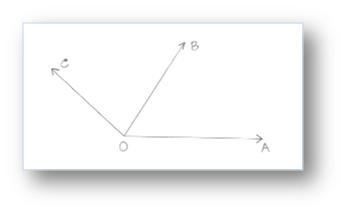
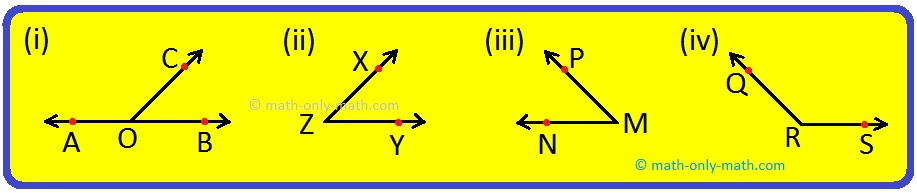
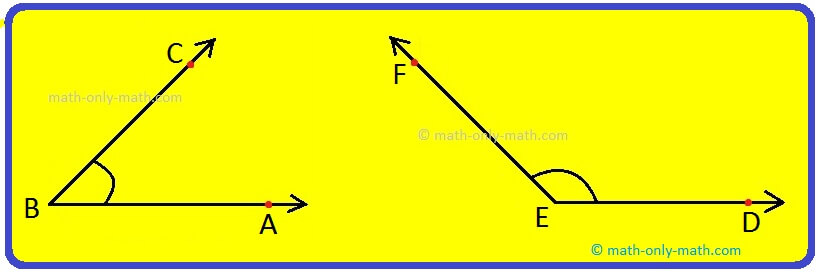
1. Which of the following figures is the example of adjacent angles?

Solution:

Figure (i) has a pair of adjacent angles.

4. Vertically Opposite Angles:

Two angles formed by two intersecting lines having no common arm are called vertically opposite angles.

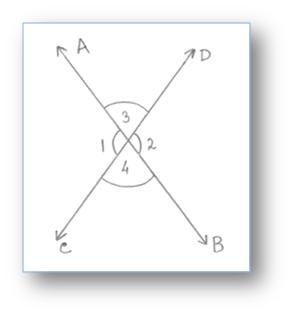
In the above given figure, two lines \(\overleftrightarrow{AB}\) and \(\overleftrightarrow{CD}\) intersect each other at a point O.

They form four angles ∠AOC, ∠COB, ∠BOD and ∠AOD in which ∠AOC and ∠BOD are vertically opposite angles. ∠COB and ∠AOD are vertically opposite angle.

∠AOC and ∠COB, ∠COB and ∠BOD, ∠BOD and ∠DOA, ∠DOA and ∠AOC are pairs of adjacent angles.

Similarly we can say that, ∠1 and ∠2 form a pair of vertically opposite angles while ∠3 and ∠4 form another pair of vertically opposite angles.

When two lines intersect, then vertically opposite angles are always equal.

∠1 = ∠2

∠3 = ∠4

Definition of Vertically Opposite Angles:

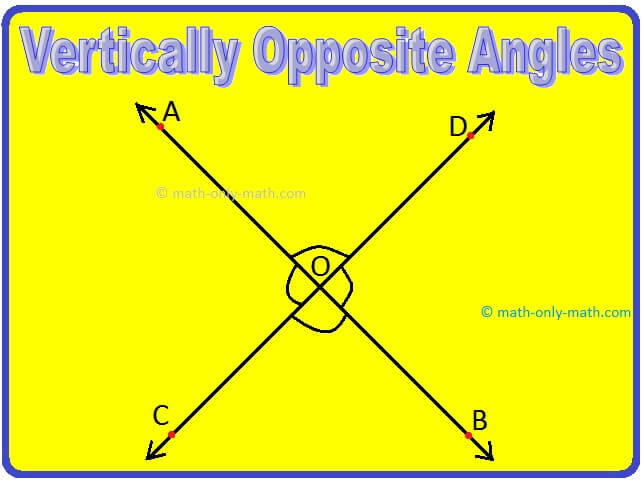
The angles opposite to the common vertex formed by the intersection of two lines are known as vertically opposite angles. 

In the above figure, if AB and CD are two intersecting lines intersecting at point O, then ∠AOD and ∠COB are vertically opposite angles.

Also, ∠AOC and ∠DOB are vertically opposite angles.

The vertically opposite angles have no common arm.

The magnitude of vertically angles are always equal.

Examples of Vertically Opposite Angles:

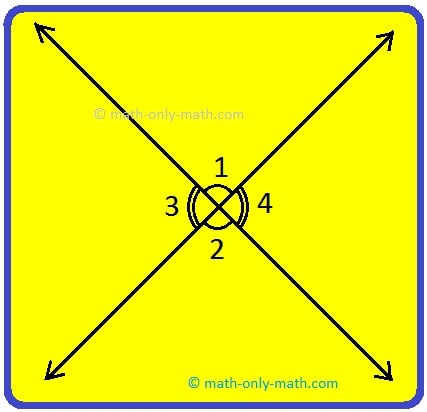
1. In the figure given below, the vertically opposite angles are marked. Are they equal?

Solution:

(∠1 and ∠2) and (∠3 and ∠4) are vertically opposite angles.

Yes, they are equal, as vertically opposite angles are always equal.

i.e., ∠1 = ∠2, ∠3 = ∠4.

5. Linear Pair:

Two adjacent angles are said to form a linear pair if their sum is 180°.

These are the pairs of angles in geometry.

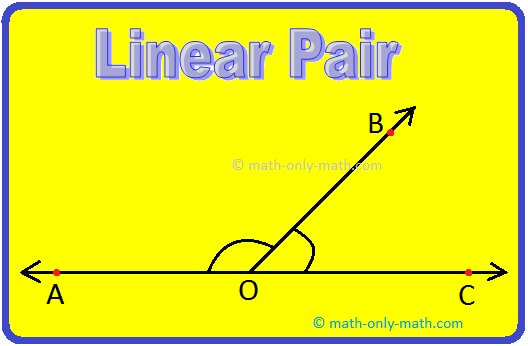
Definition of Linear Pair Angles:

A pair of adjacent angles is said to form a linear pair, if the outer arms of the angles lie on one line.

In figure, ∠AOB and ∠BOC form a linear pair, as their arms OA and OC are on the same line.

Obviously, ∠AOB + ∠BOC = 180° i.e., the sum of the measure of a linear pair is always 180°.

Examples of Linear Pair Angles:

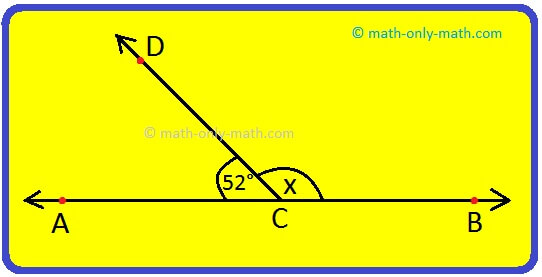
1. Find value of x in the adjacent figure.

Solution:

∠ACD + ∠DCB = 180°

52° + x = 180°

x = 128°

Worksheet on Pairs of Angles:

1. When do you say that two angles are adjacent to each other?

Answer:

1. Two angles are said to be adjacent when they have a common vertex and a common arm.

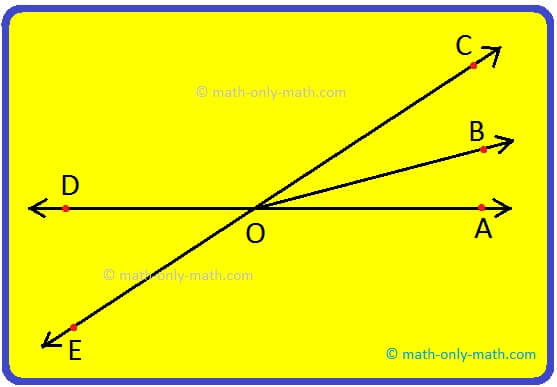
2. In the following figures, do angles B and E form a linear pair? Give Reason.

Answer:

2. Angles B and E not form a linear pair.

Two adjacent angles are said to form a linear pair if their sum is 180°.

Here angles B and E are not adjacent angles.

So, its not a linear pair.

3. An angle is equal to its complement. What is its magnitude?

Answer:

3. 45°

4. In the following figure, name the vertically opposite angle of ∠DOE.

Answer:

4. ∠AOC

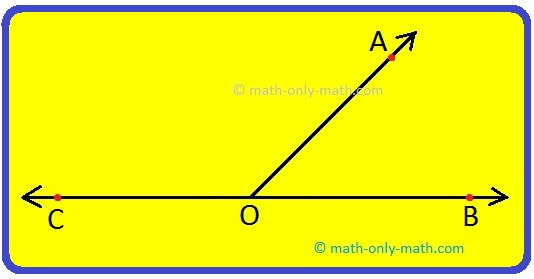
5. Fill in the blanks (with respect to the following figure):

(i) __________ and __________ are an example of a linear pair. (ii) In a linear pair, the sum of the two adjacent angles will be equal to __________.

Answer:

5. (i) ∠AOC, ∠AOB

(ii) 180°

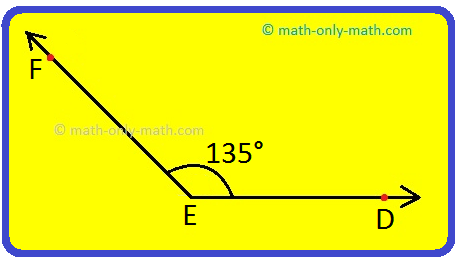
6. What is the supplement of ∠DEF?

Answer:

6. Supplement of ∠DEF = 180° - ∠DEF

                                       = 180° - 135°

                                       = 45°

7. Find out the supplements of the following angles:

(i) 90°   

(ii) 10°

(iii) 81°

Answer:

7. (i) 180° - 90° = 90° 

(ii) 180° - 10° = 170°

(iii) 180° - 81° = 99°

8. Find out the complements of the following angles:

(i) 81°

(ii) 10°

(iii) 27°

Answer:

8. (i) 90° - 81° = 9°

(ii) 90° - 10° = 80°

(iii) 90° - 27° = 63°

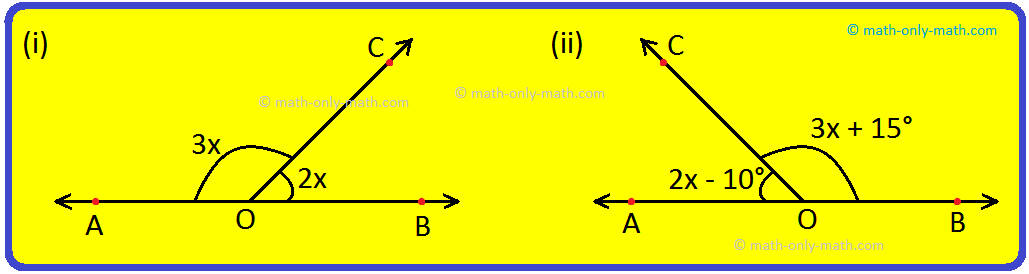
9. Find the degree measure of each angle in the linear pairs of the following figures:

Answer:

9. (i) 3x + 2x = 180°

      ⟹ 5x = 180°

      ⟹ x = 180°/5

      ⟹ x = 36°

(ii) 3x + 15° + 2x - 10° = 180°

      ⟹ 5x + 5° = 180°

      ⟹ 5x = 180° - 5°

      ⟹ 5x = 175°

      ⟹ x = 175°/5

      ⟹ x = 35°

10. In the adjoining figure, state whether (∠CAB and ∠ABD ) is a pair of adjacent angles. If not, why?

Answer:

10. They are not pair of adjacent angles. 

Two angles are said to be adjacent, if they have a common vertex and a common arm.

They have a common arm but the vertex is different.

11. An angle is \(\frac{1}{2}\) of its supplement. What is the degree measure of the angle?

Answer:

11. Let the angle is x.

The its supplement is 180° - x.

According to the question, 

x = \(\frac{1}{2}\)(180° - x)

⟹ 2x = 180° - x

⟹ 3x = 180°

⟹ x = \(\frac{180°}{3}\)

⟹ x = 60°

Therefore, the required angle is 60°.

● Angle.

Interior and Exterior of an Angle.

Measuring an Angle by a Protractor.

Types of Angles.

Pairs of Angles.

Bisecting an angle.

Construction of Angles by using Compass.

Worksheet on Angles.

Geometry Practice Test on angles.

5th Grade Geometry Page

5th Grade Math Problems

From Pairs of Angles to HOME PAGE