Subscribe to our YouTube channel for the latest videos, updates, and tips.
Interior and Exterior of an Angle
Interior and exterior of an angle is explained here.
The shaded portion between the arms BA and BC of the angle ABC can be extended indefinitely.
This portion is called the interior of the angle. X is a point in the interior of the angle. The point Y lies in the exterior of the angle.
The point Z lies on the angle.
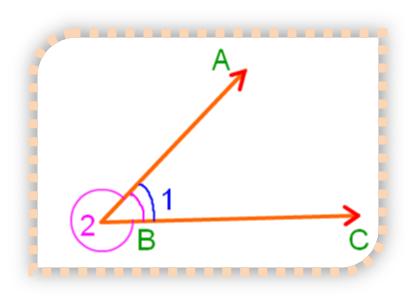
In the above figure, here ∠1 is called the interior angle because it lies inside the two arms. ∠2 is called the exterior angle. Whenever two rays meet, two angle are formed – one an interior angle and other an exterior angle. The size of an angle is measured by the amount of turn or rotation of two arms and not by how long the arms appear to be.
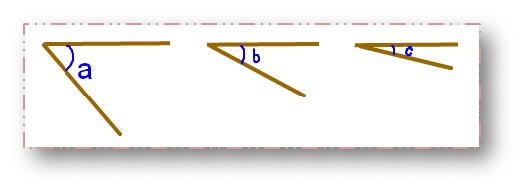
Here ∠a is greater than ∠b, ∠b is greater than ∠c.
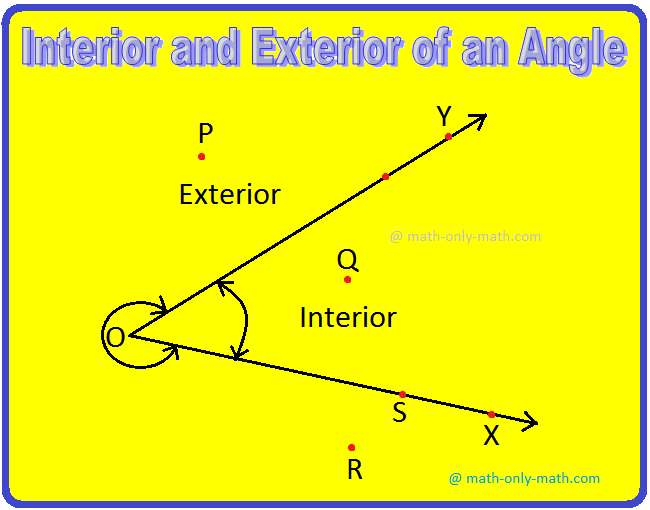
Let ∠XOY be an angle in the plane. The rays OX and OY divide all the points of the plane in three regions (as shown in the below figure).
Now, we have the following:
(i) The region shown by the shaded part is the interior of ∠XOΥ.
(ii) The region of all the points, which do not lie in the interiors well as on its arms, is called the exterior of ∠XOY.
(iii) The region of all those points which lie on the arms OX and OY is called the common boundary of the two regions.
In the above figure, points P and R are in the exterior of ∠XOY, Q is in the interior of ∠XOY and O, B, S, X, Y lie on the boundary of ∠XOY.
Notes:
1. The arms of an angle separate its interior and exterior.
2. The interior of an angle together with its boundary is called the angular region of the angle
You might like these
Types of Quadrilaterals | Properties of Quadrilateral | Parallelogram
Types of quadrilaterals are discussed here: Parallelogram: A quadrilateral whose opposite sides are parallel and equal is called a parallelogram. Its opposite angles are equal.
Worksheet on Circle |Homework on Circle |Questions on Circle |Problems
In worksheet on circle we will solve different types of question in circle. 1. The following figure shows a circle with centre O and some line segments drawn in it. Classify the line segments as radius, chord and diameter:
Worksheet on Triangle | Homework on Triangle | Different types|Answers
In the worksheet on triangle we will solve different types of questions on triangle. 1. Take three non - collinear points L, M, N. Join LM, MN and NL. What figure do you get? Name: (a)The side opposite to ∠L. (b) The angle opposite to side LN. (c) The vertex opposite to
Properties of Triangle | Angle Sum Property | Triangle Inequality Prop
We will discuss here about the properties of triangle. Property 1: Relation between the measures of three angles of triangle: Draw three triangles on your not book. Name them as ∆PQR, ∆ABC and ∆LMN.
Bisecting an Angle | Bisecting an Angle by Using a Protractor | Rules
Bisecting an angle means dividing it into two equal angles. The ray which bisects an angle is known as its bisector. ∠LMN is the given angles. Fold the paper so that LM falls along MN
Worksheet on Angles | Questions on Angles | Homework on Angles
In worksheet on angles you will solve different types of questions on angles. Classify the following angles into acute, obtuse, right and reflex angle: (i) 35° (ii) 185° (iii) 90°
Perpendicular Lines | What are Perpendicular Lines in Geometry?|Symbol
In perpendicular lines when two intersecting lines a and b are said to be perpendicular to each other if one of the angles formed by them is a right angle. In other words, Set Square Set Square If two lines meet or intersect at a point to form a right angle, they are
What are Parallel Lines in Geometry? | Two Parallel Lines | Examples
In parallel lines when two lines do not intersect each other at any point even if they are extended to infinity. What are parallel lines in geometry? Two lines which do not intersect each other
Classification of Triangle | Types of Triangles |Isosceles|Equilateral
Triangles are classified in two ways: (i) On the basis of sides and, (ii) On the basis of angles.In classification of triangle there are six elements in a triangle, that is, three sides and three angles. So, classification of triangle is done on the base of these elements.
Construction of Angles by using Compass, Construction of Angles
In construction of angles by using compass we will learn how to construct different angles with the help of ruler and compass.
Construction of Perpendicular Lines by Using a Protractor, Set-square
Construction of perpendicular lines by using a protractor is discussed here. To construct a perpendicular to a given line l at a given point A on it, we need to follow the given procedure
Pairs of Angles | Complementary Angles | Supplementary Angles|Adjacent
Pairs of angles are discussed here in this lesson. 1. Complementary Angles: Two angles whose sum is 90° are called complementary angles and one is called the complement of the other.
Circle | Interior and Exterior of a Circle | Radius|Problems on Circle
A circle is the set of all those point in a plane whose distance from a fixed point remains constant. The fixed point is called the centre of the circle and the constant distance is known
Relation between Diameter Radius and Circumference |Problems |Examples
Relation between diameter radius and circumference are discussed here. Relation between Diameter and Radius: What is the relation between diameter and radius? Solution: Diameter of a circle is twice
Practice Test on Circle | Quiz on Circle | Question and Test on Circle
Geometry practice test on circle, the questions we practiced and discussed under worksheets on circle are given here in geometry practice test.
● Angle.
Interior and Exterior of an Angle.
Measuring an Angle by a Protractor.
Construction of Angles by using Compass.
Geometry Practice Test on angles.
5th Grade Math Problems
From Interior and Exterior of an Angle to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Division of a Decimal by a Decimal |Decimal Division|Dividing Decimals
May 10, 25 02:36 AM
Division of a decimal by a decimal are discussed here. 1. 14.7 ÷ 2.1 Solution: 14.7 ÷ 2.1 [Count the number of decimal digits in the divisor and we observe that after decimal there is 1 -
Expanded form of Decimal Fractions |How to Write a Decimal in Expanded
May 07, 25 01:48 AM
Decimal numbers can be expressed in expanded form using the place-value chart. In expanded form of decimal fractions we will learn how to read and write the decimal numbers. Note: When a decimal is mi… -
Dividing Decimals Word Problems Worksheet | Answers |Decimals Division
May 07, 25 01:33 AM
In dividing decimals word problems worksheet we will get different types of problems on decimals division word problems, dividing a decimal by a whole number, dividing a decimals and dividing a decima… -
How to Divide Decimals? | Dividing Decimals by Decimals | Examples
May 06, 25 01:23 AM
Dividing Decimals by Decimals I. Dividing a Decimal by a Whole Number: II. Dividing a Decimal by another Decimal: If the dividend and divisor are both decimal numbers, we multiply both the numbers by… -
Multiplying Decimal by a Whole Number | Step-by-step Explanation|Video
May 06, 25 12:01 AM
Multiplying decimal by a whole number is just same like multiply as usual. How to multiply a decimal by a whole number? To multiply a decimal by a whole number follow the below steps
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.