5th Grade Triangle

Triangle is one of the basic shape in geometry.

A triangle is a simple closed figure made up of three line segments. It has three sides and three vertices. It is represented by the symbol ∆. 

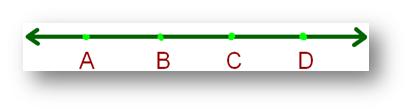
We know that we can mark many points on any given line.

Three or more points which lie on the same line are called collinear points.

Above, points A, B, C and D which lie on the same line collinear points.

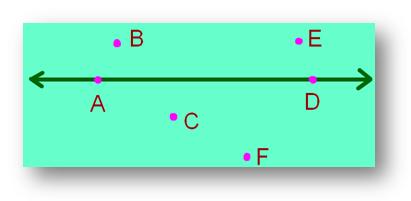
But in the figure below, only two points A and D lied on the line. Points B, E, C and F do not lie on that line.

Hence, these points A, B, C, D, E, F are called non - collinear points.

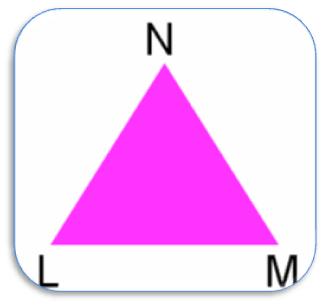
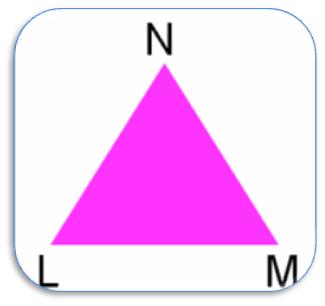
If we join three non - collinear points L, M and N lie on the plane of paper, then we will get a closed figure bounded by three line segments LM, MN and NL. This closed figure is called a Triangle.

The three line segments of a triangle are also known as sides of the triangle.

This triangle is named as ∆ LMN with its side as LM, MN and NL and three vertices as L, M and N.

The three angles named as ∠ LMN, ∠MNL and ∠ NLM are the angles of the triangle.

Three angles are denoted by ∠M, ∠N and ∠L respectively.

The three angles and the three sides of a triangle are together called the six parts or elements of the triangle.

Thus, a closed figure bounded by three line segments is called a triangle. 

∆ is the symbol to denote a triangle.

Note: A triangle has 6 elements: Three sides and three angles.

Thus 1. A triangle is named in three different ways

(i) ∆LMN or (ii) ∆MNL or (iii) ∆NLM

2. Vertices of ∆LMN are L, M, N.

3. Angles of ∆LMN are ∠L, ∠M and ∠N.

4. Line segments of ∆LMN are LM, MN, NL.

The side LM is the base of the ∆ NLM. ∠N opposite to the base LM is called the Vertical angle of the triangle.

∠N and ∠M adjacent to the base LM are called Base angles.

If we add up the three sides of a triangle, we get its perimeter.

Thus the perimeter of the ∆LMN = LM + MN + NL.

Note: Therefore, a triangle has:

Three line segments,

Three vertices,

Three angles.

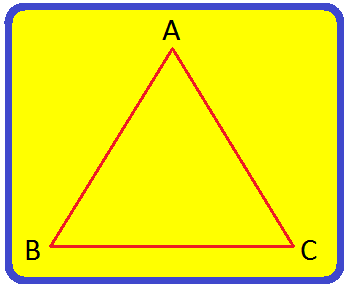
In the given figure, we see that triangle ABC has three sides AB, BC and CA which are line segments. A, B and C are called the vertices of the triangle.

Remember:

A triangle is a closed figure bounded by three line segments.

A triangle has three angles. ∠ABC, ∠ACB and ∠BAC are the three angles of the above Triangle. We represent these angles as ∠A, ∠B and ∠C too.

So, we can conclude that a triangle has the following elements.

(i) Three vertices

(ii) Three sides

(iii) Three angles

We denote a triangle as ∆.

● Triangle.

Classification of Triangle.

Properties of Triangle.

Worksheet on Triangle.

To Construct a Triangle whose Three Sides are given.

To Construct a Triangle when Two of its Sides and the included Angles are given.

To Construct a Triangle when Two of its Angles and the included Side are given.

To Construct a Right Triangle when its Hypotenuse and One Side are given.

Worksheet on Construction of Triangles.

5th Grade Geometry Page

5th Grade Math Problems

From 5th Grade Triangle to HOME PAGE