Classification of Triangle

In classification of triangle there are six elements in a triangle, that is, three sides and three angles. So, classification of triangle is done on the base of these elements.

Triangles are classified in two ways:

(i) On the basis of sides and,

(ii) On the basis of angles.

Classification of Triangles on the Basis of Sides:

A triangle is a polygon with three sides. It has three sides and three vertices. The sum of the angles of a triangle is 180°.

Classification of triangles based on their sides. A triangle in which all the sides are equal is called an equilateral triangle. A triangle in which any two sides are equal is called an isosceles triangle. If none of its sides are equal it is called a scalene triangle. Now, let us classify triangles based on their angles.

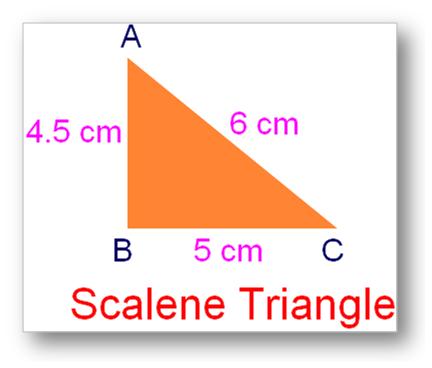
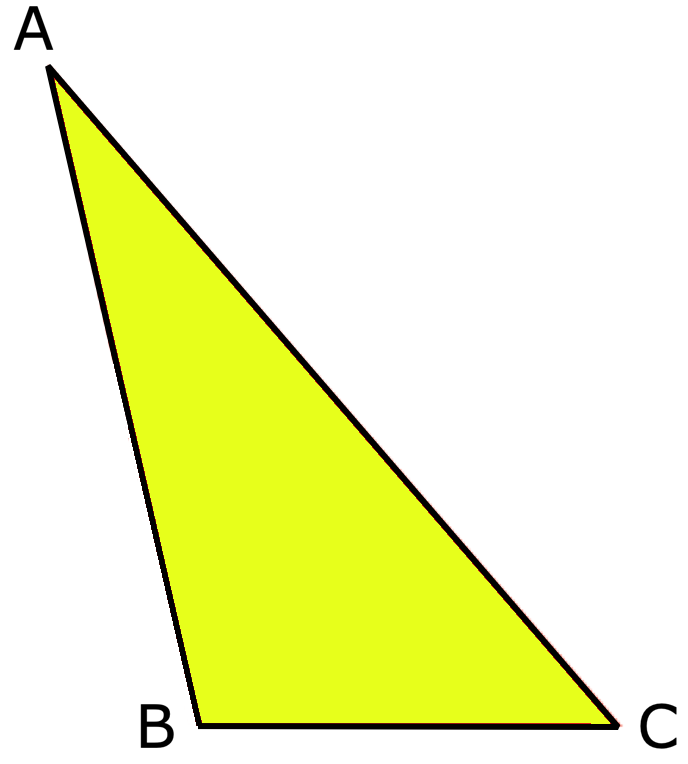
1. Scalene Triangle:

A triangle in which all the three sides are unequal in length is called a scalene triangle.

AC > BC >AB

6 cm > 5 cm > 4.5 cm.

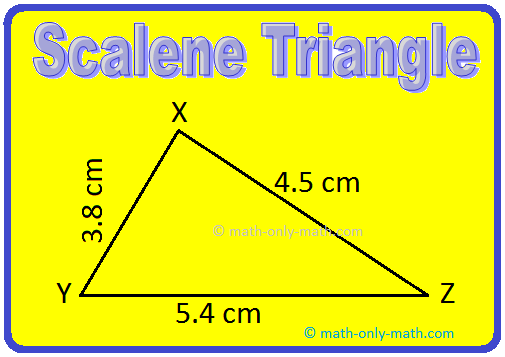
Definition of Scalene Triangle:

A triangle with unequal sides in length is called a scalene triangle. 

In figure, ∆XYZ such that XY ≠ YZ ≠ XZ.

Therefore, ∆XYZ is a scalene triangle.

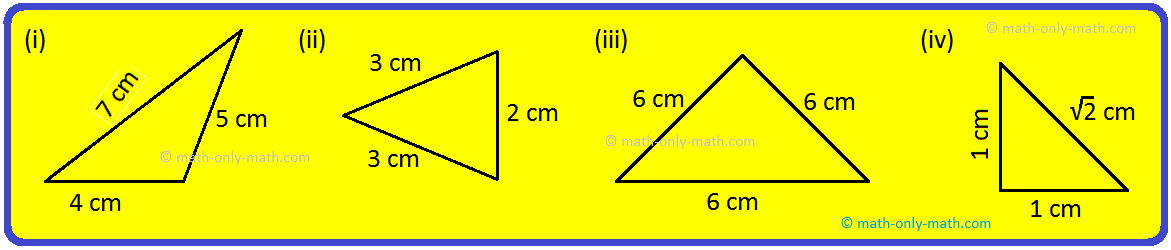
Examples on Scalene Triangle:

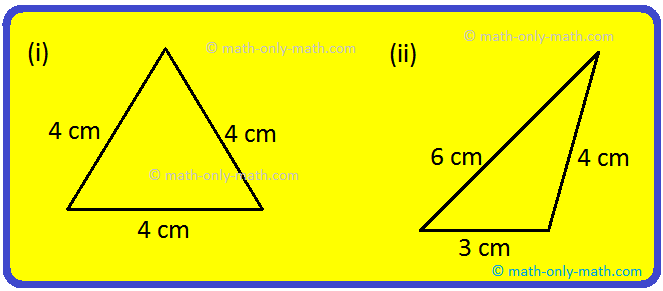
1. Which of the following is scalene triangle?

Solution:

Option (i) is a scalene triangle, as its all sides are unequal.

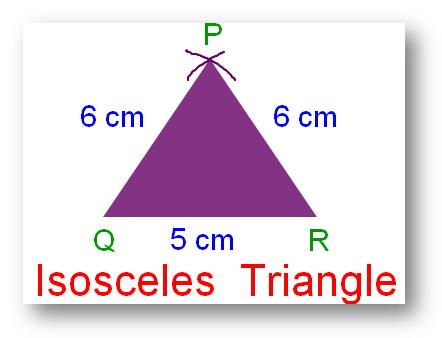
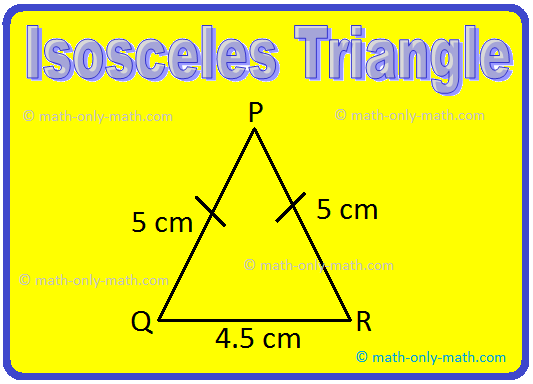
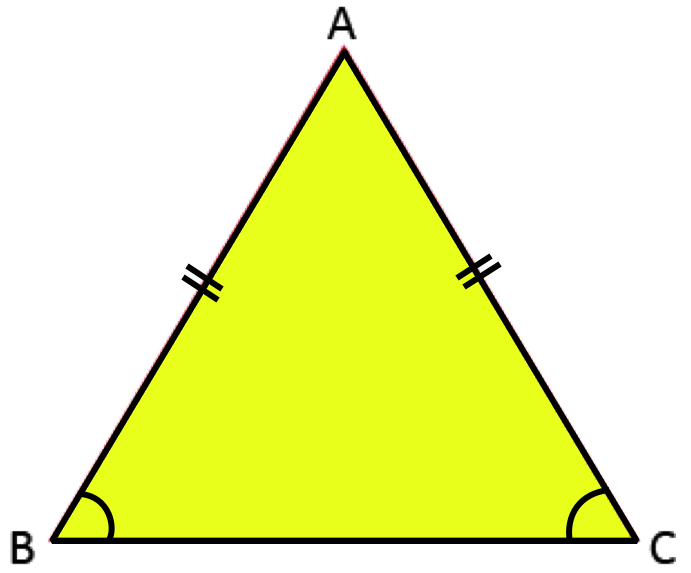
2. Isosceles Triangle:

A triangle in which two of its sides are equal is called isosceles triangle.

PQ = PR = 6 cm.

Definition of Isosceles Triangle:

If any two sides of a triangle are equal in length, it is called an isosceles triangle.

In triangle PQR, PQ = RP

Therefore, ∆PQR is an isosceles triangle.

Examples on Isosceles Triangle:

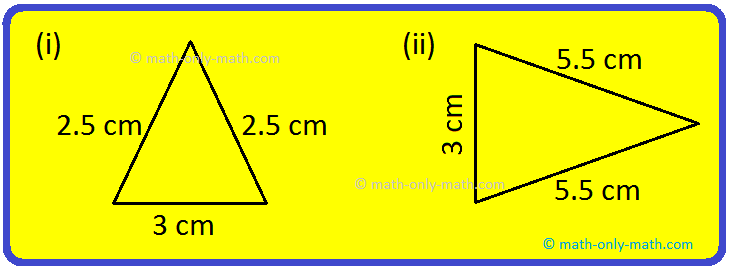
1. State whether the following is/are isosceles triangle or not.

Solution:

Fig. (i) and (ii) are isosceles triangles, as their two sides are equal.

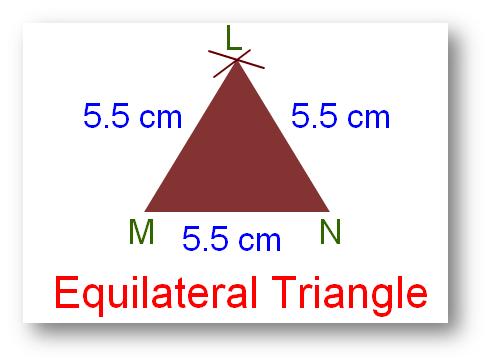
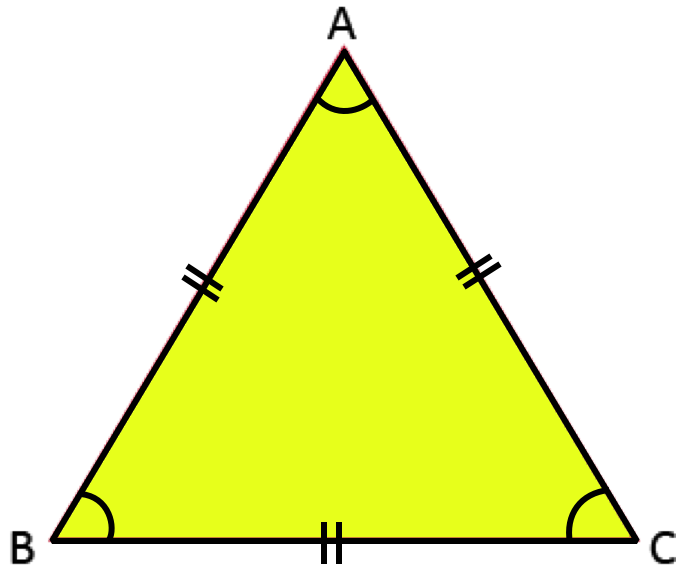
3. Equilateral Triangle:

A triangle in which have all its three sides equal in length is called an equilateral triangle.

LM = MN = NL = 5.5 cm

Definition of Equilateral Triangle:

If all the three sides of a triangle are equal in length, it is called an equilateral triangle.

In ∆PQR, PQ = QR = RP.

Therefore, ∆PQR is an equilateral triangle.

Examples on Equilateral Triangle:

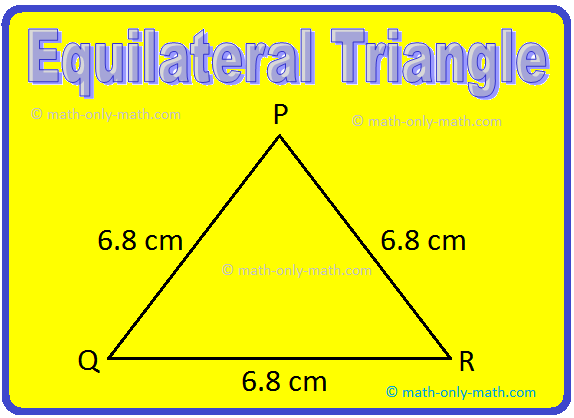
1. State whether the following triangles are equilateral or not:

Solution:

Fig. (i) is an equilateral triangle, whose all three sides are equal.

Fig. (ii) is not an equilateral triangle, because its all three sides are not equal.

Classification of Triangles on the Basis of Angles:

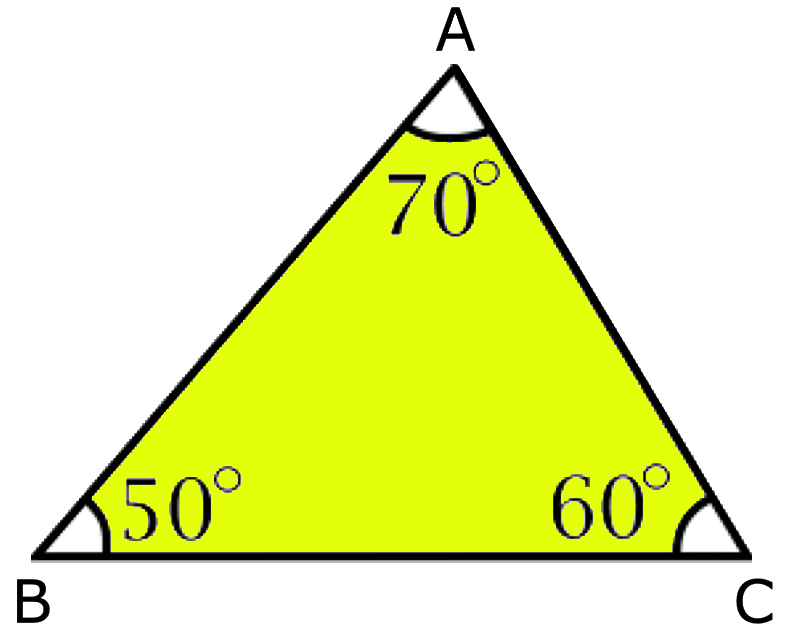
1. Acute Triangle:

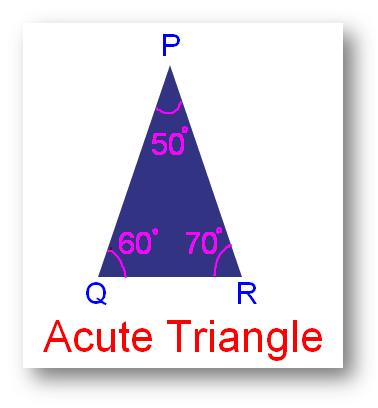
A triangle which has all the three angles acute that is, less than 90°, is called an acute angled triangle or acute triangle.

In other words, a triangle is which all the three angles are acute is called an acute-angled triangle. 

In the given figure ∠A, ∠B and ∠C are acute angle. Thus, ∆ABC is an acute-angled triangle.

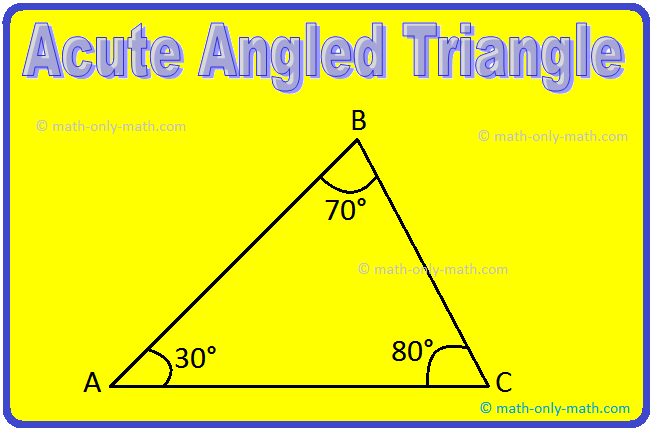
Definition of Acute Angled Triangle:

An acute angled triangle is a triangle whose all the three angles
are acute (i.e., less than 90°).

In figure, ∆ABC is an acute angled triangle.

Examples on Acute Angled Triangle:

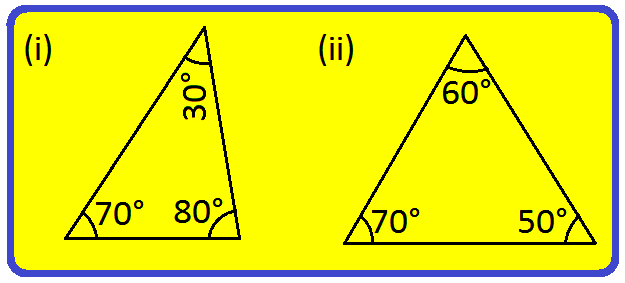
1. State whether the triangles shown in the following figures are acute-angled triangle or not.

Solution:

Figures (i) and (ii) are acute-angled triangles, as all the three angles are less than 90° in both.

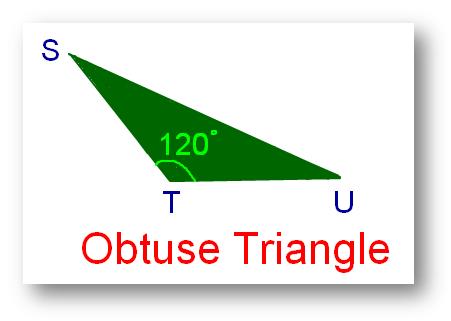
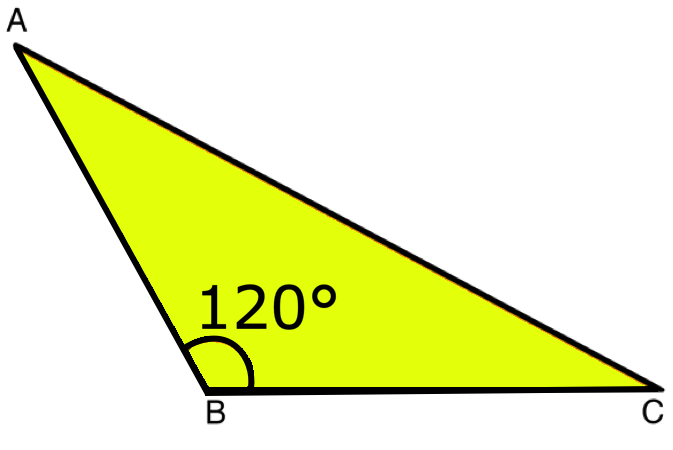
2. Obtuse Triangle:

A triangle whose one angle is obtuse or more than 90° but less than 180° is called an obtuse angled triangle or obtuse triangle.

A triangle is which one of its angles is measuring more than 90° is known as an obtuse-angled triangle. 

In the above figure ∠STU = 120°. Thus, ∆STU is an obtuse-angled triangle.

Definition of Obtuse Angled Triangle:

An obtuse angled triangle is a triangle, if its one angle is obtuse (i.e., more than 90°). 

In figure, ∆ABC is obtuse angled triangle, as ∠A is obtuse.

Examples on Obtuse Angled Triangle:

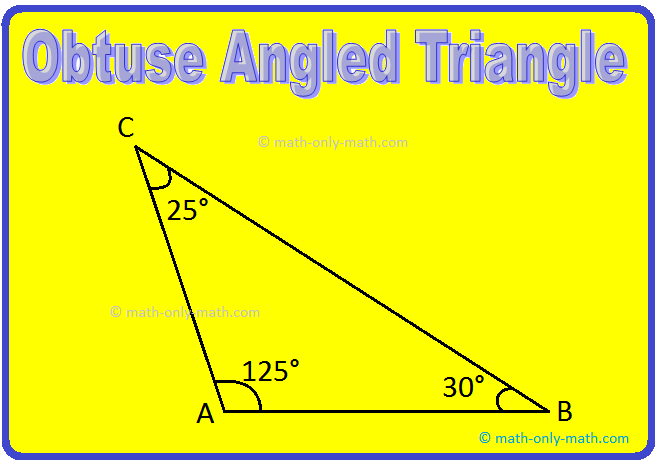
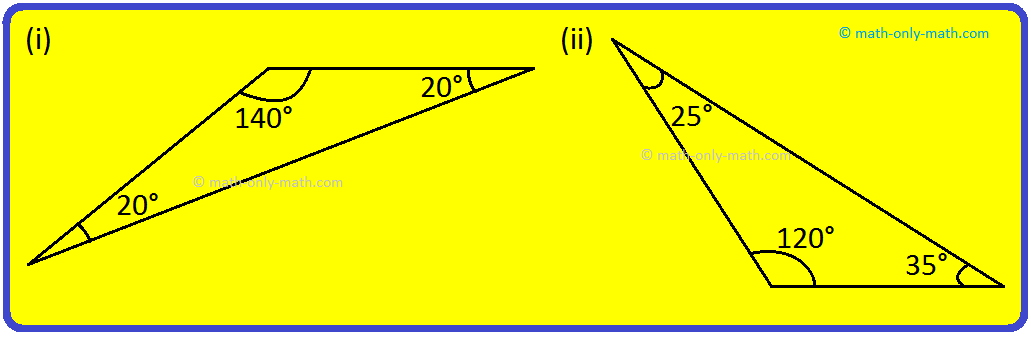
1. State whether the triangles shown in the following figures are obtuse-angled or not:

Solution:

Figures (i) and (ii) are obtuse-angled triangles, as one of the angles is more than 90° in both.

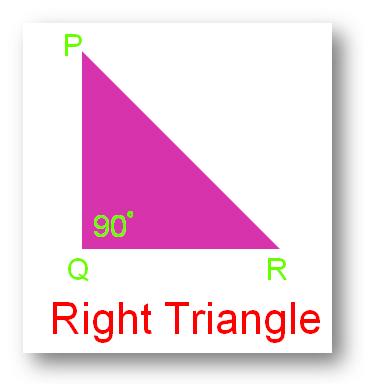
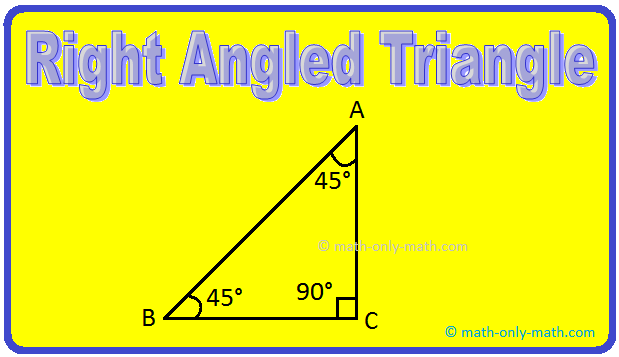
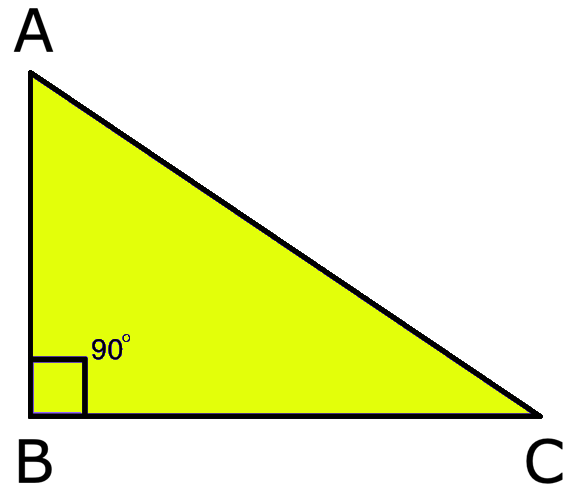
3. Right Triangle:

A triangle whose one angles is a right angle (that is 90°) is called a right angled triangle or right angle.

In other words, a triangle in which any one of the three angles is exactly 90°, is known as a right-angled triangle. 

In the above figure ∠PQR = 90°. Thus, ∆PQR is a right-angled triangle.

Definition of Right Angled Triangle:

A triangle is called a right angled triangle, if its one angle is 90° or a right angle. 

In figure, ABC is a right angled triangle, as ∠C = 90°.

Questions and Answers on Classification of Triangle:

I. Fill in the blanks:

(i) The triangle with equal sides is …………………….

(ii) A ……………………. triangle has all sides of different length.

(iii) Each angle of equilateral triangle is …………………….

(iv) An ……………………. triangle has two equal sides.

(v) In obtuse angled triangle one angle is ……………………. 90°.

(vi) Each angle of an acute triangle is ……………………. than 90°.

Answers:

(i) Equilateral

(ii) Scalene

(iii) Equal

(iv) Isosceles

(v) Greater than

(vi) Less than

II. Classify the following triangle:

(i) Sides of triangle are 4 cm, 4 cm and 7 cm

(ii) Angles of triangle is 90°, 60° and 30°

(iii) Angles of triangle is 110°, 40° and 30°

(iv) Sides of triangle are 5 cm, 13 cm and 12 cm

(v) Angles of triangle is 60°, 60° and 60°

Answers:

(i) Isosceles triangle

(ii) Right-angled triangle

(iii) Obtuse-angled triangle

(iv) Scalene triangle

(v) Equilateral triangle

● Triangle.

Classification of Triangle.

Properties of Triangle.

Worksheet on Triangle.

To Construct a Triangle whose Three Sides are given.

To Construct a Triangle when Two of its Sides and the included Angles are given.

To Construct a Triangle when Two of its Angles and the included Side are given.

To Construct a Right Triangle when its Hypotenuse and One Side are given.

Worksheet on Construction of Triangles.

5th Grade Geometry

5th Grade Math Problems

From Classification of Triangle to HOME PAGE