Construction of Perpendicular Bisector

Here we will learn how to construct a perpendicular bisector of a line segment.

The perpendicular bisector of a line segment is the line that is perpendicular to the line segment at its mid-point.

In the adjoining Fig., \(\overleftrightarrow{PO}\) is the perpendicular bisector of \(\overline{AB}\) bisecting \(\overline{AB}\) at O i.e., \(\overline{AO}\) = \(\overline{BO}\)

First Method: To Draw the Perpendicular Bisector with the Help of Transparent Tapes

Working Rules To Draw the Perpendicular Bisector:

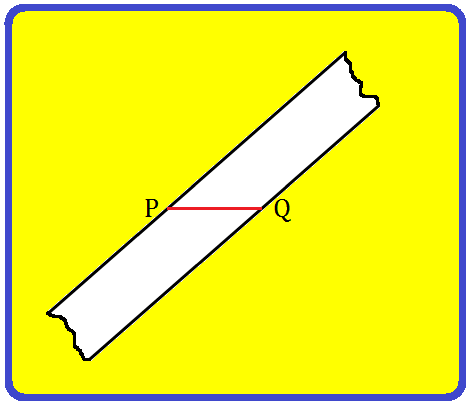
Step I: Draw a line segment PQ.

Step II: Paste a strip of a transparent rectangular taps diagonally across the end-points P and Q as shown in the figure.

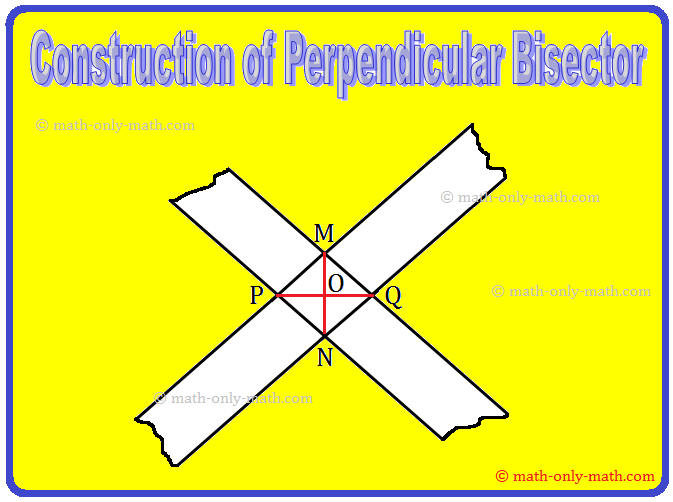
Step III: Repeat the process as in step-2 by placing another taps over P and Q just diagonally across the previous one. Thus, two strips cross at M and N.

Step IV: Join M and N to get \(\overline{MN}\) and \(\overline{PQ}\) as the required perpendicular bisectors of each other.

Second Method: To Draw the Perpendicular Bisector using Ruler and Compasses

Working Rules To Draw the Perpendicular Bisector:

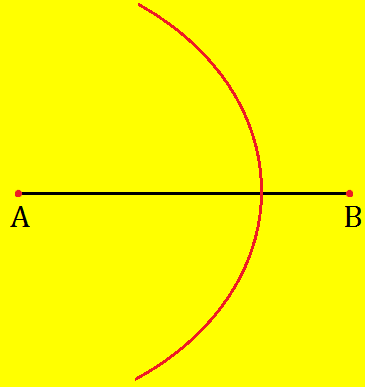
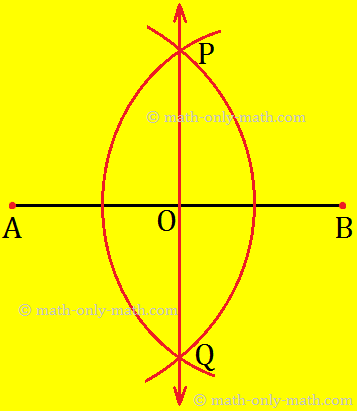
Step I: Draw a line segment AB of any length.

Step II: Using compass, draw an arc with A as centre and a radius more than half the length of \(\overline{AB}\)

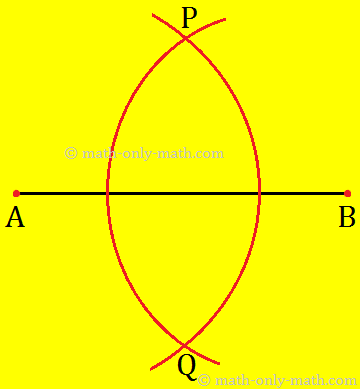
Step III: With B as a centre and same radius as in step-II, draw another arc to intersect the previous arc at P and Q.

Step III: Join P and Q to get \(\overleftrightarrow{PQ}\). It cuts AB at O. This line PQ bisects the given line segment AB at O. i.e. \(\overline{AO}\) = \(\overline{BO}\)

What would happen?

In steps II and III above, what would happen, if we take less than half of the length as radius and draw arcs?

Solved Examples on Construction of Perpendicular Bisector:

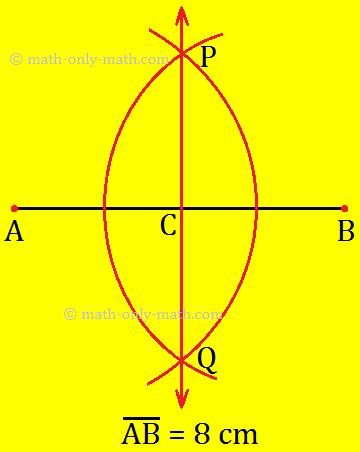
1. Draw a line segment AB of length 8 cm. Using compass, divide it into four equal parts.

Solution:

Step I: Draw a line segment AB = 8 cm and draw a perpendicular bisector using steps given in the Working Rules.

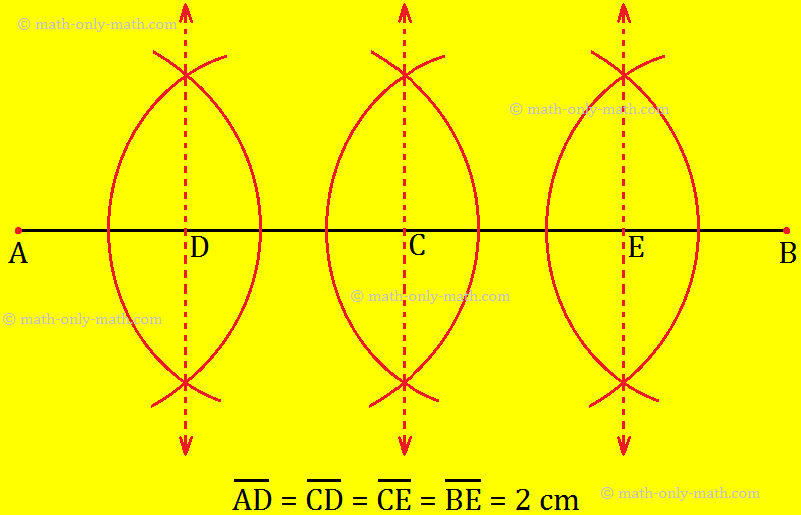
Step II: In step I, we have divided \(\overline{AB}\) into two equal parts \(\overline{AC}\) and \(\overline{BC}\) Similarly, draw the perpendicular bisectors of \(\overline{AC}\) and overline BC separately. 

Now, we obtain four equal parts of \(\overline{AB}\)

i.e., \(\overline{AD}\) = \(\overline{CD}\) = \(\overline{CE}\) = \(\overline{BE}\) = 2 cm .

Worksheet on Construction of Perpendicular Bisector:

1. Draw a line segment of 8.5 cm and draw its perpendicular bisector.

2. Divide a line segment of length 8 cm into four equal parts using compass.

3. Draw a circle of radius 5 cm. Draw two chords on it. Constrct the perpendicular bisector of these chords. Where do they meet?

4. Draw a triangle. Construct three perpendicular bisectors on each of its side. Check whether all three bisectors meet at one point.

5. Divide a line segment of length 10 cm into four equal parts using compass.

5th Grade Geometry

5th Grade Math Problems

From CConstruction of Perpendicular Bisector of a Line Segment to HOME PAGE

New! Comments

Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.

Share this page: What’s this?

FacebookXPinterestWhatsAppReddit

ShareFacebookXPinterestWhatsAppReddit