Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Home | About Us | Contact Us | Privacy | Math Blog
Position of a Point with Respect to a Circle
We will learn how to find the position of a point with respect to a circle.
A point (x1, y1) lies outside, on or inside a circle S = x2 + y2 + 2gx + 2fy + c = 0 according as S1 > = or <0, where S1 = x12 + y12 + 2gx1 + 2fy1 + c.
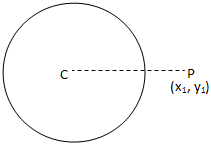
Let P (x1, y1) be a given point, C (-g , -f) be the centre and a be the radius of the given circle.
We need to find the position of the point P (x1, y1) with respect to the circle S = x2 + y2 + 2gx + 2fy + c = 0.
Now, CP = √(x1+g)2+(y1+f)2
Therefore, the point
(i) P lies outside the circle x2 + y2 + 2gx + 2fy + c = 0 if CP > the radius of the circle.
i.e., √(x1+g)2+(y1+f)2 > √g2+f2−c
⇒ (x1+g)2+(y1+f)2 > g2 + f2 - c
⇒ x12 + 2gx1 + g2 + y12 + 2fy1 + f2 > g2 + f2 – c
⇒ x12 + y12 + 2gx1 + 2fy1 + c > 0
⇒ S1 > 0, where S1 = x12 + y12 + 2gx1 + 2fy1 + c.
(ii) P lies on the circle x2 + y2 + 2gx + 2fy + c = 0 if CP = 0.
i.e., √(x1+g)2+(y1+f)2 = √g2+f2−c
⇒ (x1+g)2+(y1+f)2 = g2 + f2 - c
⇒ x12 + 2gx1 + g2 + y12 + 2fy1 + f2 = g2 + f2 – c
⇒ x12 + y12 + 2gx1 + 2fy1 + c = 0
⇒ S1 = 0, where S1 = x12 + y12 + 2gx1 + 2fy1 + c.
(iii) P lies inside the circle x2 + y2 + 2gx + 2fy + c = 0 if CP < the radius of the circle.
i.e., √(x1+g)2+(y1+f)2 < √g2+f2−c
⇒ (x1+g)2+(y1+f)2 < g2 + f2 - c
⇒ x12 + 2gx1 + g2 + y12 + 2fy1 + f2 < g2 + f2 – c
⇒ x12 + y12 + 2gx1 + 2fy1 + c < 0
⇒ S1 < 0, where S1 = x12 + y12 + 2gx1 + 2fy1 + c.
Again, if the equation of the given circle be (x - h)2 + (y
- k)2 = a2 then the coordinates of the centre C (h, k) and the radius of the circle
= a
We need to find the position of the point P (x1, y1) with respect to the circle (x - h)2 + (y - k)2= a2.
Therefore, the point
(i) P lies outside the circle (x - h)2 + (y - k)2 = a2 if CP > the radius of the circle
i.e., CP > a
⇒ CP2 > a2
⇒ (x1 - h)2 + (y1 - k)2 > a2
(ii) P lies on the circle (x - h)2 + (y - k)2 = a2 if CP = the radius of the circle
i.e., CP = a
⇒ CP2 = a2
⇒ (x1 - h)2 + (y1 - k)2 = a2
(iii) P lies inside the circle (x - h)2 + (y - k)2 = a2 if CP < the radius of the circle
i.e., CP < a
⇒ CP2 < a2
⇒ (x1 - h)2 + (y1 - k)2 < a2
Solved examples to find the position of a point with respect to a given circle:
1. Prove that the point (1, - 1) lies within the circle x2 + y2 - 4x + 6y + 4 = 0, whereas the point (-1, 2) is outside the circle.
Solution:
We have x2 + y2 - 4x + 6y + 4 = 0 ⇒ S = 0, where S = x2 + y2 - 4x + 6y + 4
For the point (1, -1), we have S1 = 12 + (-1)2 - 4 ∙1 + 6 ∙ (- 1) + 4 = 1 + 1 - 4 - 6 + 4 = - 4 < 0
For the point (-1, 2), we have S1 = (- 1 )2 + 22 - 4 ∙ (-1) + 6 ∙ 2 + 4 = 1 + 4 + 4 + 12 + 4 = 25 > 0
Therefore, the point (1, -1) lies inside the circle whereas (-1, 2) lies outside the circle.
2. Discuss the position of the points (0, 2) and (- 1, - 3) with respect to the circle x2 + y2 - 4x + 6y + 4 = 0.
Solution:
We have x2 + y2 - 4x + 6y + 4 = 0 ⇒ S = 0 where S = x2 + y2 - 4x + 6y + 4
For the point (0, 2):
Putting x = 0 and y = 2 in the expression x2 + y2 - 4x + 6y + 4 we have,
S1 = 02 + 22 - 4 ∙ 0 + 6 ∙ 2 + 4 = 0 + 4 – 0 + 12 + 4 = 20, which is positive.
Therefore, the point (0, 2) lies within the given circle.
For the point (- 1, - 3):
Putting x = -1 and y = -3 in the expression x2 + y2 - 4x + 6y + 4 we have,
S1 = (- 1)2 + (- 3)2 - 4 ∙ (- 1) + 6 ∙ (- 3) + 4 = 1 + 9 + 4 - 18 + 4 = 18 - 18 = 0.
Therefore, the point (- 1, - 3) lies on the given circle.
● The Circle
- Definition of Circle
- Equation of a Circle
- General Form of the Equation of a Circle
- General Equation of Second Degree Represents a Circle
- Centre of the Circle Coincides with the Origin
- Circle Passes through the Origin
- Circle Touches x-axis
- Circle Touches y-axis
- Circle Touches both x-axis and y-axis
- Centre of the Circle on x-axis
- Centre of the Circle on y-axis
- Circle Passes through the Origin and Centre Lies on x-axis
- Circle Passes through the Origin and Centre Lies on y-axis
- Equation of a Circle when Line Segment Joining Two Given Points is a Diameter
- Equations of Concentric Circles
- Circle Passing Through Three Given Points
- Circle Through the Intersection of Two Circles
- Equation of the Common Chord of Two Circles
- Position of a Point with Respect to a Circle
- Intercepts on the Axes made by a Circle
- Circle Formulae
- Problems on Circle
11 and 12 Grade Math
From Position of a Point with Respect to a Circle to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
5th Grade Pie Chart | Definition of Pie Chart | Construction |Examples
Jul 31, 25 05:12 PM
Data can also be represented in a circle. This method, to represent data, is called a pie chart. Let us understand this method with the help of an example. -
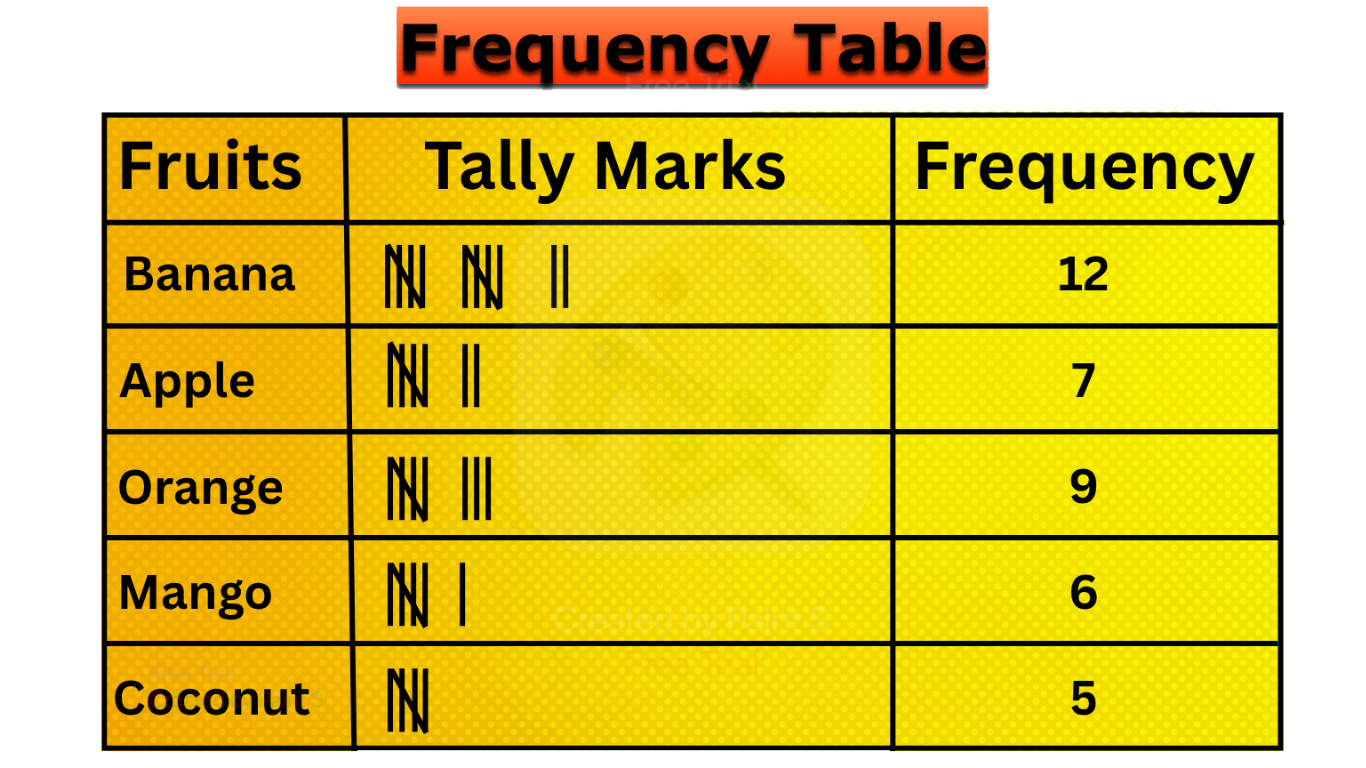
Frequency Distribution |Tally Marks |Frequency Distribution Table
Jul 31, 25 12:23 PM
What is frequency distribution?The number of times a particular observation occurs in a given data is called its frequency. In 7ᵗʰ grade and 8ᵗʰ grade frequency distribution, -
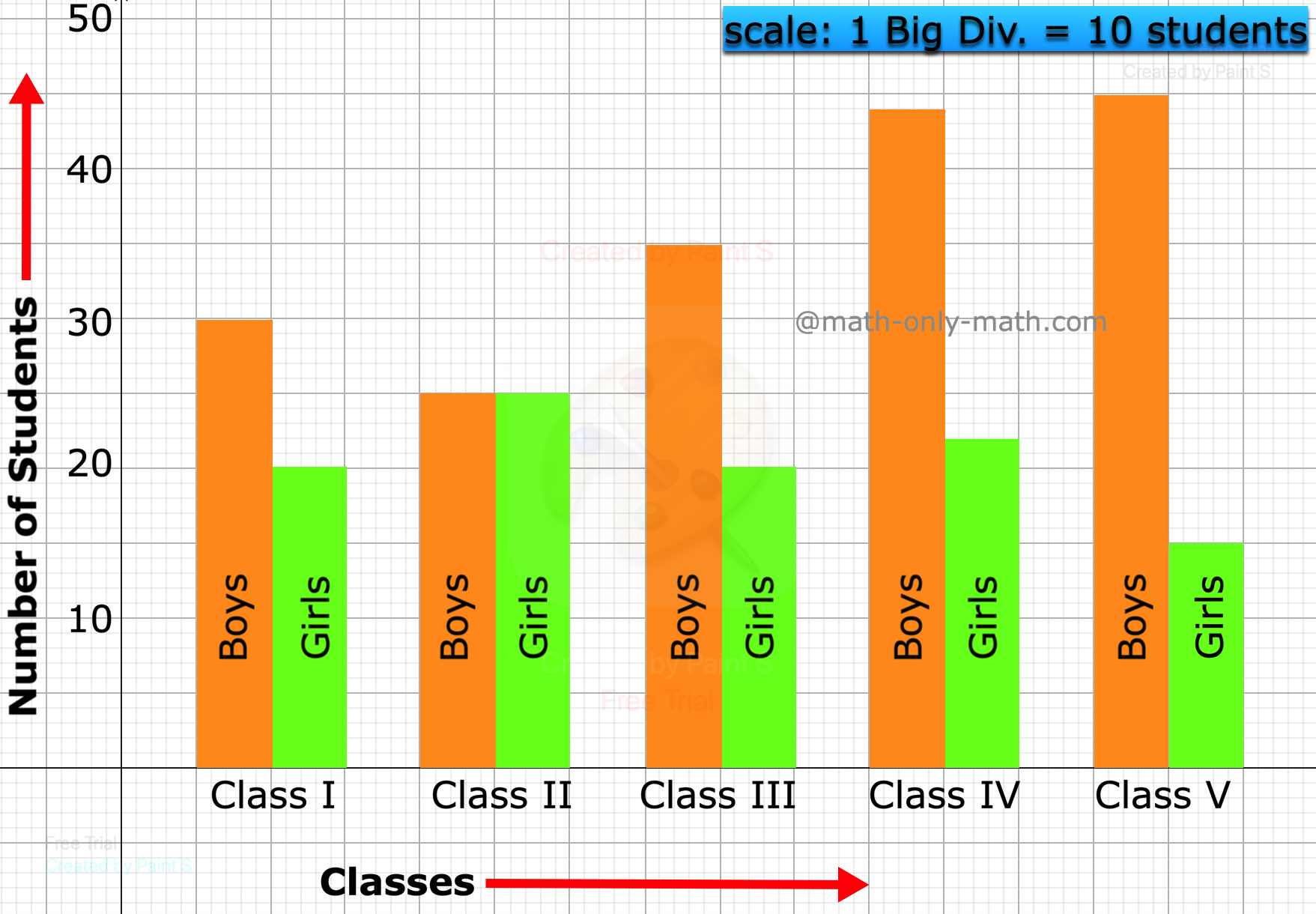
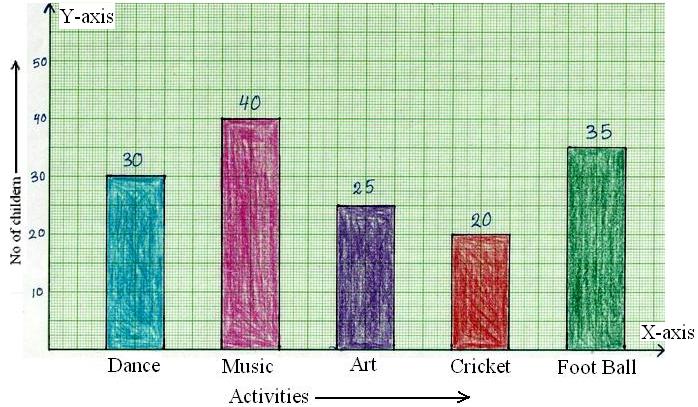
5th Grade Bar Graph | Definition | Interpret Bar Graphs|Free Worksheet
Jul 31, 25 05:16 AM
We learn how to represent the data on the bar graph. Data can be represented by bars (like rectangle) whose lengths represent numerical values. One can use horizontal or vertical bars. Instead of rect… -
Construction of Bar Graphs | Examples on Construction of Column Graph
Jul 31, 25 03:35 AM
Now we will discuss about the construction of bar graphs or column graph. In brief let us recall about, what is bar graph? Bar graph is the simplest way to represent a data. In consists of rectangular… -
Successor and Predecessor | Successor of a Whole Number | Predecessor
Jul 29, 25 12:59 AM
The number that comes just before a number is called the predecessor. So, the predecessor of a given number is 1 less than the given number. Successor of a given number is 1 more than the given number…


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.