Division of Whole Numbers

Division of whole numbers is discussed here step by step.

1. Division is repeated subtraction.

(a) 25 ÷ 5 = 5

(Repeated Subtraction)

(i) 25 - 5 = 20

(ii) 20 - 5 = 15

(iii) 15 - 5 =10

(iv) 10 - 5 = 5

(v) 5 - 5 = 0 

(b) 10 ÷ 2 = 5

(Repeated Subtraction)

(i) 10 - 2 = 8

(ii) 8 - 2 = 6

(iii) 6 - 2 = 4

(iv) 4 - 2 = 2

(v) 2 - 2 = 0 



(c) 50 ÷ 10 = 5

(Repeated Subtraction)

(i) 50 - 10 = 40.

(ii) 40 - 10 = 30

(iii) 30 - 10 = 20

(iv) 20 - 10 = 10

(v) 10 - 10 = 0 



2. Division is the inverse of multiplication.

(a) (i) 12 × 10 = 120

(ii) 120 ÷ 10= 12

(iii) 120 ÷ 12 = 10 



(b) (i) 25 × 5 = 125

(ii) 125 ÷ 5 = 25

(iii) 125 ÷ 25 = 5 



3. Relation between Dividend, Divisor, Quotient and Remainder is.

Dividend = Divisor × Quotient + Remainder

To understand the relation between dividend, divisor, quotient and remainder let us follow the following examples:

(a) Divide 537809 by 35 and find the quotient and remainder.

We need to divide the dividend i.e. 537809 by the divisor i.e. 35 to get the quotient and remainder.

5 cannot be divided by 35 as 5 < 35. So, we will move to the next digit of the dividend i.e. 3 and now we have 53 which can be divided by 35 as 53 > 35. We first divide 53 by 35. 35 into 53 is 1 leaving 18.

Then we bring down the next digit of the dividend i.e. 7 and we have 187. Now we divide 187 by 35 so, 35 into 187 is 5 leaving 12.

Again we bring down the next digit of the dividend i.e. 8 and we have 128. Now we divide 128 by 35 so, 35 into 128 is 3 leaving 23.

Similarly, again we bring down the next digit of the dividend i.e. 0 and we have 230. Now we divide 230 by 35 so, 35 into 230 is 6 leaving 20.

And at last we bring down the last digit of the dividend i.e. 9 and we have 209. So, we divide 209 by 35 then, 35 into 209 is 5 leaving 34.

Check the answer of the division:

Dividend = Divisor × Quotient + Remainder

537809 = 35 × 15365 + 34

537809 = 537775 + 34

537809 = 537809

(b) Divide 86228364 by 2768 and check the answer.

We need to divide the dividend i.e. 86228364 by the divisor i.e. 2768 to get the quotient and remainder.

8 cannot be divided by 2768 as 8 < 2768. So, we will move to the second digit of the dividend i.e. 6 and now we have 86 which cannot be divided by 2768 as 86 < 2768. So, we will move to the third digit of the dividend i.e. 2 and now we have 862 which also cannot be divided by 2768 as 862 < 2768. So, we will move to the fourth digit of the dividend i.e. 2 and now we have 8622 which can be divided by 2768 as 8622 > 2768. We first divide 8622 by 2768. 2768 into 8622 is 3 leaving 318.

Then we bring down the fifth digit of the dividend i.e. 8 and we have 3188. Now we divide 3188 by 2768 so, 2768 into 3188 is 1 leaving 420.

Again we bring down the sixth digit of the dividend i.e. 3 and we have 4203. Now we divide 4203 by 2768 so, 2768 into 4203 is 1 leaving 1435.

Similarly, again we bring down the seventh digit of the dividend i.e. 6 and we have 14356. Now we divide 14356 by 2768 so, 2768 into 14356 is 5 leaving 516.

And at last we bring down the last digit of the dividend i.e. 4 and we have 5164. So, we divide 5164 by 2768 then, 2768 into 5164 is 1 leaving 2396.

Now to check the answer of the division:

Dividend = Divisor × Quotient + Remainder

86228364 = 2768 × 31151 + 2396

86228364 = 86225968 + 2396

86228364 = 86228364

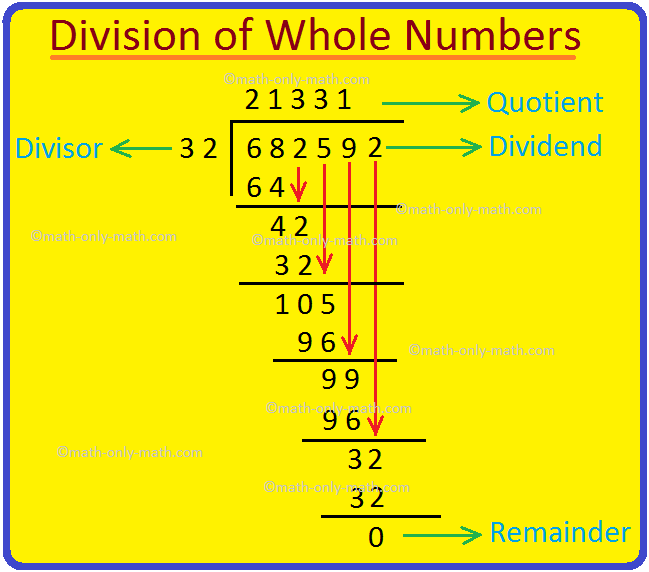
4. Divide 682592 by 32 and verify the answer.

Solution:

Hence, 682592 ÷ 32 =21331

Now to check the answer of the division:

Divisor × Quotient + Remainder = Dividend

    32   ×   21331   +      0         = 682592

Division of Large Numbers

We follow the usual method of division to divide large numbers.

Let us consider some examples.

Division of 7-Digit Number by 1-Digit Number (Indian Numbering System)

1. Divide 12,46,560 by 8

Solution:

Therefore, the quotient is 1,55,820.

Division of 7-Digit Number by 2-Digit Number (International Numbering System)

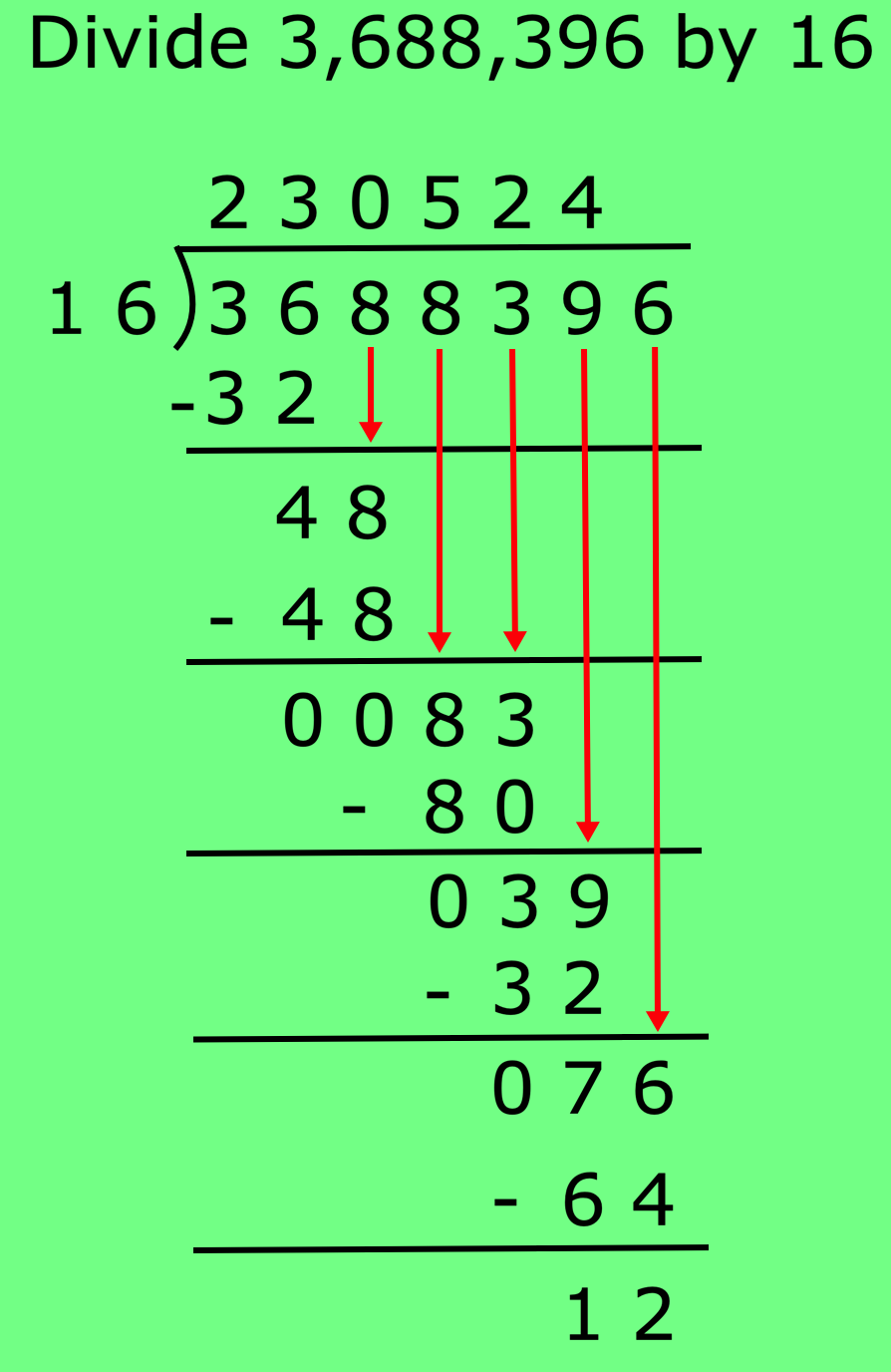
2. Divide 3,688,396 by 16

Solution:

Therefore, the quotient is 230,524 and the remainder is 12.

Division of 7-Digit Number by 3-Digit Number (Indian Numbering System)

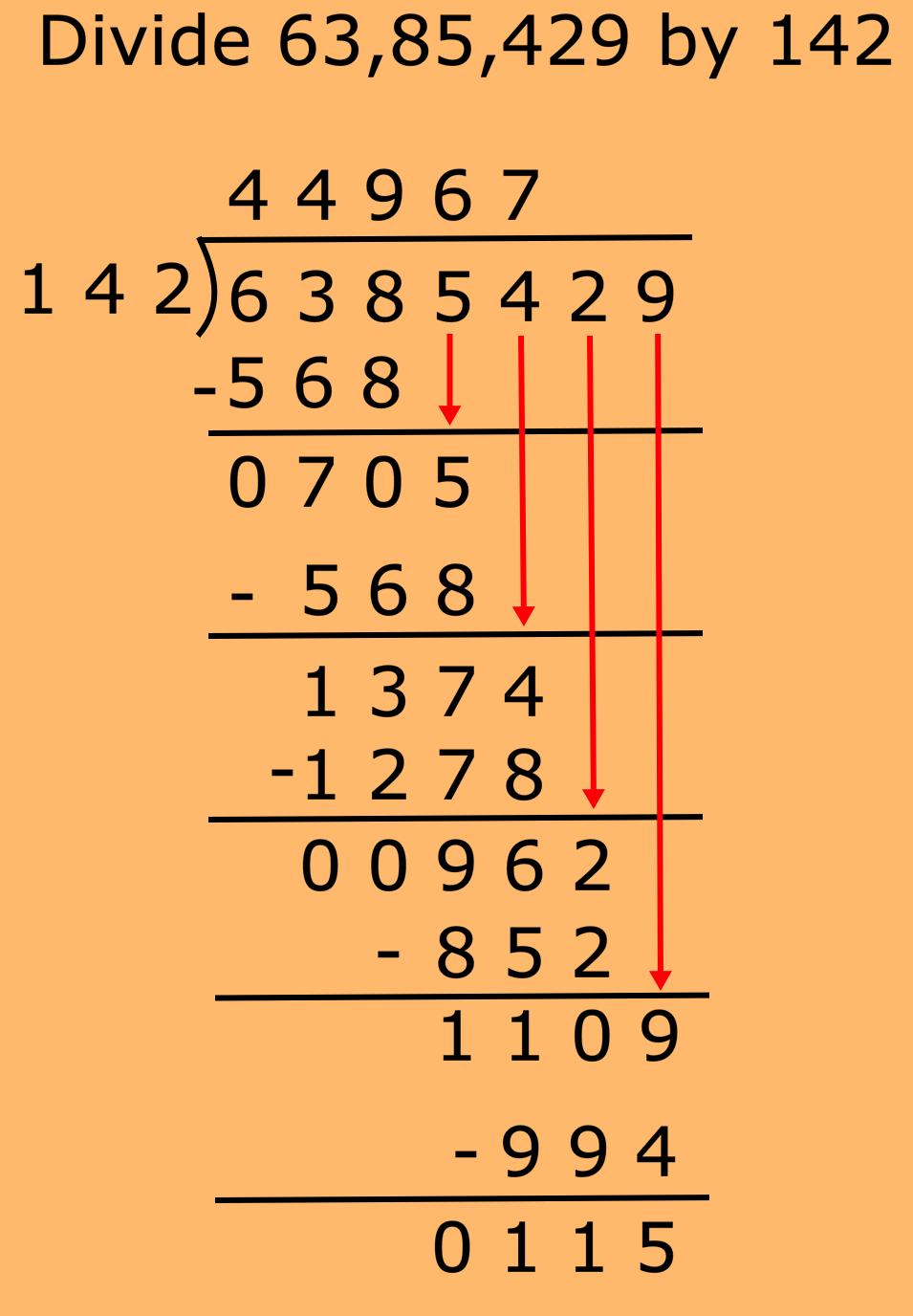
3. Divide 63,85,429 by 142

Solution:

Therefore, the quotient is 44,967 and the remainder is 115.

Division of 7-Digit Number by 3-Digit Number (International Numbering System)

4. Divide 3,295,552 by 250

Solution:

Therefore, the quotient is 13,182 and the remainder is 52.

Division by Numerals Ending With Zeroes:

We know that division is the inverse operation of multiplication. When we divide a number by 10, 100 or 1000, we take away as many zeroes from dividend as in the divisor.

For example:

1. Divide by 10

60 ÷ 10 = 6

600 ÷ 10 = 60

6000 ÷ 10 = 600

60000 ÷ 10 = 6000

2. Divide by 100

600 ÷ 100 = 6

6000 ÷ 100 = 60

60000 ÷ 100 = 600

600000 ÷ 100 = 6000

3. Divide by 1000

6000 ÷ 1000 = 6

60000 ÷ 1000 = 60

600000 ÷ 1000 = 600

6000000 ÷ 1000 = 6000

Questions and Answers on Division of Whole Numbers:

I. Find the quotient and check the answers in each of the following:

(i) 22786 ÷ 3

(ii) 389458 ÷ 7

(iii) 6872419 ÷ 24

(iv) 7714592 ÷ 32

(v) 9600729 ÷ 84

(vi) 11682000 ÷ 125

(vii) 66921036 ÷ 170

(viii) 6017635 ÷ 580

(ix) 7654981 ÷ 53

Answers:

(i) Quotient = 7595; Remainder = 1.

(ii) Quotient = 55636; Remainder = 6.

(iii) Quotient = 286350; Remainder = 19.

(iv) Quotient = 241081; Remainder = 0.

(v) Quotient = 114294; Remainder = 33.

(vi) Quotient = 93456; Remainder = 0.

(vii) Quotient = 393653; Remainder = 26.

(viii) Quotient = 10375; Remainder = 135.

(ix) Quotient = 144433; Remainder = 32.

2. Find the quotient and remainder for the given.

(i) 8703364 ÷ 10

(ii) 6933453 ÷ 10000

(iii) 459827 ÷ 100

(iv) 7768232 ÷ 100000

(v) 5672861 ÷ 1000

(vi) 97367140 ÷ 10000

Answers:

(i) Quotient = 870336; Remainder = 4.

(ii) Quotient = 693; Remainder = 3453.

(iii) Quotient = 4598; Remainder = 27.

(iv) Quotient = 77; Remainder = 68232.

(v) Quotient = 5672; Remainder = 861.

(vi) Quotient = 9736; Remainder = 7140.

3. Fill In the blanks.

(i) 4928831 ÷ 1 = ________

(ii) 6582110 × ________ = 6582110

(iii) 5082240 ÷ 10 = ________

(iv) ________ × 0 = 0

(v) 7433925 ÷ 7433925 = ________

(vi) 8953022 + ________ = 8953023

(vii) 3800452 × (0 × 883245) = ________

Answers:

(i) 4928831

(ii) 1

(iii) 508224

(iv) Any number

(v) 1

(vi) 1

(vii) 0

Word Problems on Division of Whole Numbers:

4. 125896 tiles are to be loaded in 8 vehicles equally. How many tiles are loaded in each vehicle?

Answer: 15737 tiles

5. 3792780 voters are to be equally distributed in 18 blocks. How many voters will there be in each block?

Answer: 210710 voters

● Operations On Whole Numbers

• Addition Of Whole Numbers.
• Word Problems on Addition and Subtraction of Whole Numbers
• Subtraction Of Whole Numbers.
• Multiplication Of Whole Numbers.
• Properties Of Multiplication.
• Division Of Whole Numbers.
• Properties Of Division.
• Word Problems on Multiplication and Division of Whole Numbers
• Worksheet on Addition and Subtraction of Large Numbers
• Worksheet on Multiplication and Division of Large Numbers
• Worksheet on Operations On Whole Numbers

5th Grade Math Problems

From Division of Whole Numbers to HOME PAGE