Relation between Cartesian and Polar Co-Ordinates

Here we will learn to find the relation between Cartesian and Polar Co-Ordinates.

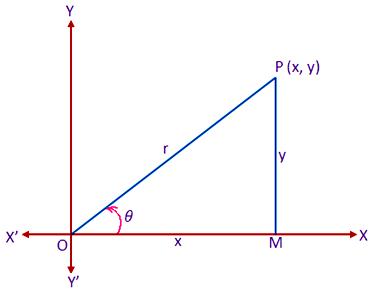
Let XOX’ and YOY’ be a set of rectangular Cartesian axes of polar Co-ordinates through the origin O. now, consider a polar Co-ordinates system whose pole and initial line coincide respectively with the origin O and the positive x-axis of the Cartesian system. Let P be any point on the plane whose Cartesian and polar Co-ordinates are (x, y) and (r, θ) respectively. Draw PM perpendicular to OX. Then we have,

OM = x, PM = y, OP = r and < MOP = θ

Now, from the right-angled triangle MOP we get,

x/r = cos θ     or, x = r cos θ     …… (1)

                and

y/r = sin θ     or, y = r sin     …… (2)

Using (1) and (2) we can find Cartesian Co-ordinates (x, y) of the point whose polar Co-ordinates (r, θ) are given.

Again, from the right angled triangle OPM we get,

r² = x² + y²

or, r = √(x² + y²) …… (3)

and tan θ = y/x or, θ = tan$^{-1}$ y/x ……… (4) 

Using (3) and (4) we can find the polar Co-ordinates (r, θ) of the points whose Cartesian Co-ordinates (x, y) are given.

Note:

If the Cartesian Co-ordinates (x, y) of a point are given then to find the value of the vectorial angle θ by the transformation equation θ = tan$^{-1}$ y/x we should note the quadrant in which the point (x, y) lies.

Examples on the relation between Cartesian and Polar Co-Ordinates.

1. The cartesian co-ordinates of a point are (- 1, -√3); find its polar co-ordinates. 

Solution: 

If the pole and initial line of the polar system coincide with the origin and positive x-axis respectively of the cartesian system and the cartesian and polar co-ordinates of a point are ( x, y ) and ( r, θ ) respectively, then 

    x = r cos θ and y= r sin θ. 

In the given problem, x = -1 and y = -√3

Therefore, r cos θ = -1 and r sin θ = -√3 

Therefore, r² Cos² θ + r² sin² = (- 1)² + (-√3)²

And tan θ = (r sin θ)/(r cos θ) = (-√3)/(-1) = √3 = tan π/3

Or, tan θ =tan(π+ π/3) [Since, the point (- 1, - √3) lise in the third quadrant] 

Or, tan θ = tan 4π/3 

Therefore, θ = 4π/3 

Therefore, the polar co-ordinates of the point (- 1, - √3) are (2, 4π/3). 

2. Find the cartesian co-ordinates of the point whose polar co-ordinates are (3, - π/3). 

Solution:

Let (x, y) be the cartesian co-ordinates of the point whose polar co-ordinates are (3, - π/3). Then,

x= r cos θ = 3 cos (- π/3) = 3 cos π/3 = 3 ∙ 1/2 = 3/2

and y = r sin θ = 3 sin (- π/3) = 3 sin π/3 = -(3√3)/2.

Therefore, the required cartesian co-ordinates of the point (3, -π/3) are (3/2, -(3√3)/2)

3. Transfer, the cartesian form of equation of the curve x² - y² = 2ax to its polar form. 

Solution:

Let OX and OY be the rectangular cartesian axes and the pole and the initial line of the polar system coincide with O and OX respectively. If (x, y) be the cartesian co-ordinates of the point whose polar co-ordinates are (r, θ), then we have,

x = r cos θ and y = r sin θ.

Now, x² - y² = 2ax

or, r² cos² θ - r² sin² θ = 2a.r cos θ

or, r² (cos² θ - sin² θ) = 2ar cos θ

or, r cos 2 θ = 2a cos θ (Since, r ≠0)

which is the required polar form of the given cartesian equation.

4. Transform the polar form of equation $r^{\frac{1}{2}}$ = $a^{\frac{1}{2}}$

 cos θ/2 to its cartesian form. 

Solution:

Let OX and OY be the rectangular cartesian axes and the pole and the initial line of the polar system coincide with O and OX respectively. If (x, y) be the cartesian co-ordinates of the point whose polar co-ordinates are (r, θ), then we have,

x = r cos θ and y = r sin θ.

Clearly, x² + y²

= r² cos² θ + r² sin² θ

= r²

Now, $r^{\frac{1}{2}}$ = $a^{\frac{1}{2}}$ cos θ/2

or, r = a cos² θ/2 (squaring both sides)

or, 2r = a ∙ 2 cos² θ/2

or, 2r = = a(1 + cosθ); [Since, cos² θ/2 = 1 + cosθ]

or, 2r² = a(r + r cosθ) [multiplying by r (since, r ≠0)]

or, 2(x² + y ²) = ar + ax [r² = x² + y² and r cos θ = x]

or, 2x² + 2y² - ax = ar

or, (2x² + 2y² - ax)² = a²r² [Squaring both sides]

or, (2x² + 2y² - ax)² = a² (x² + y²),

which is the required cartesian form of the given polar form of equation.

● Co-ordinate Geometry 

• What is Co-ordinate Geometry?
  
• Rectangular Cartesian Co-ordinates
  
• Polar Co-ordinates
  
• Relation between Cartesian and Polar Co-Ordinates
  
• Distance between Two given Points
  
• Distance between Two Points in Polar Co-ordinates
  
• Division of Line Segment: Internal & External
  
• Area of the Triangle Formed by Three co-ordinate Points
  
• Condition of Collinearity of Three Points
  
• Medians of a Triangle are Concurrent
  
• Apollonius' Theorem
  
• Quadrilateral form a Parallelogram 
  
• Problems on Distance Between Two Points 
  
• Area of a Triangle Given 3 Points
  
• Worksheet on Quadrants
  
• Worksheet on Rectangular – Polar Conversion
  
• Worksheet on Line-Segment Joining the Points
  
• Worksheet on Distance Between Two Points
  
• Worksheet on Distance Between the Polar Co-ordinates
  
• Worksheet on Finding Mid-Point
  
• Worksheet on Division of Line-Segment
  
• Worksheet on Centroid of a Triangle
  
• Worksheet on Area of Co-ordinate Triangle
  
• Worksheet on Collinear Triangle
  
• Worksheet on Area of Polygon
  
• Worksheet on Cartesian Triangle

11 and 12 Grade Math 

From Relation between Cartesian and Polar Co-Ordinates to HOME PAGE